Теория Эконометрика. 1. Типы переменных в эконометрических моделях
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
1. Типы переменных в эконометрических моделях. По отношению к выбранной спецификации все экономические переменные объекта подразделяются на: Эндогенные (зависимые) – экономические переменные, значения которых определяются (объясняются) внутри модели в результате взаимодействия соотношений, образующих модель. Экзогенные (независимые) – экономические переменные, значения которых определяются вне данной модели. * При наличии хотя бы одной экзогенной переменной модель называется открытой, в противном случае – замкнутой. Лаговые переменные – экзогенные или эндогенные переменные, датированные предыдущими моментами времени и находящиеся в уравнении с текущими переменными. Предопределенные – переменные, выступающие в роли факторов-аргументов или объясняющих переменных (лаговые эндогенные, лаговые экзогенные, текущие экзогенные). 2. Спецификация парной линейной регрессионной модели, предпосылки Гаусса-Маркова. Эконометрическая модель со спецификацией вида 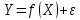 , где Y – эндогенная (зависимая) переменная; Х – экзогенная (независимая) переменная (регрессор); , где Y – эндогенная (зависимая) переменная; Х – экзогенная (независимая) переменная (регрессор); 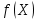 – детерминированная составляющая эндогенной переменной (уравнение регрессии), полностью объясняемая значением экзогенной переменной; – детерминированная составляющая эндогенной переменной (уравнение регрессии), полностью объясняемая значением экзогенной переменной; 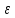 - случайная составляющая эндогенной переменной (случайное возмущение), которая не может быть объяснена значением Х, называется регрессионной моделью. Она является парной, если эндогенная переменная зависит только от одного регрессора. - случайная составляющая эндогенной переменной (случайное возмущение), которая не может быть объяснена значением Х, называется регрессионной моделью. Она является парной, если эндогенная переменная зависит только от одного регрессора. В модели парной линейной регрессии эту зависимость между переменными представляют в виде: 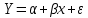 Например, 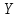 - расходы фирмы, - расходы фирмы, 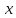 - объем выпущенной продукции за месяц. Тогда - объем выпущенной продукции за месяц. Тогда 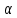 - условно-постоянные расходы, - условно-постоянные расходы, 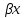 - условно-переменные расходы. - условно-переменные расходы. Относительно вектора случайных возмущений принимаются следующие предпосылки - условия Гаусса-Маркова: 1) Математическое ожидание вектора возмущений равно нулю (1 предпосылка), т.е. случайное возмущение в среднем не оказывает влияния на эндогенную переменную: 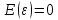 . .2) Дисперсия возмущений не зависит от номера наблюдения (возмущение гомоскедастично -2 предпосылка): 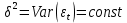 . .3) Ковариация между значениями возмущений в различных наблюдениях равна 0 (возмущение не автокоррелировано – 3 предпосылка): 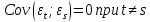 . .4) Ковариация между регрессором и случайным возмущением равна 0 (4 предпосылка): 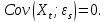 5) Возмущения имеют совместное нормальное распределение (5 предпосылка) 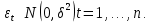 3. Теорема Гаусса - Маркова. Если: 1) модель правильно специфицирована, т.е. зависимость вида 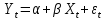 действительно существует; действительно существует;2) 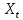 являются детерминированными величинами и не равны между собой; являются детерминированными величинами и не равны между собой;3) 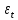 – случайные величины, причем: – случайные величины, причем: 3. 1) 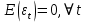 3. 2) 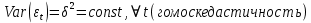 3. 3) C 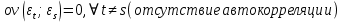 Тогда МНК оценки 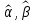 являются: являются:линейными по Y несмещенными эффективными оценками параметров 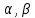 , т. е. имеют наименьшую дисперсию (эффективны) в классе всех линейных несмещенных оценок. , т. е. имеют наименьшую дисперсию (эффективны) в классе всех линейных несмещенных оценок. 4. Спецификация множественной линейной регрессионной модели в матричной форме. Матричная форма 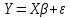 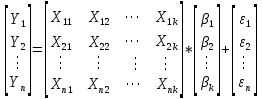 Обозначения: n – число наблюдений; k – число параметров; матрица регрессоров Х – детерминированная полного ранга: rank(X)=k * Первый столбец матрицы при наличии в спецификации свободного члена: 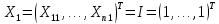 n,1 5. Оценка параметров множественной регрессионной модели методом наименьших квадратов в матричной форме. Оценка параметров классической модели множественной линейной регрессии производится методом наименьших квадратов (МНК) и состоит в решении системы нормальных уравнений для множественной регрессии. Критерий отбора: 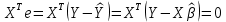 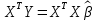 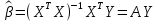 где 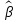 – вектор оценок параметров модели; A – детерминированная матрица, определяемая через матрицу регрессоров. Одним из достоинств МНК является линейность МНК-оценок. Полученный результат подтверждает это свойство. – вектор оценок параметров модели; A – детерминированная матрица, определяемая через матрицу регрессоров. Одним из достоинств МНК является линейность МНК-оценок. Полученный результат подтверждает это свойство. 6. Основные числовые характеристики вектора оценок параметров классической множественной регрессионной модели. Вектор оценок параметров модели 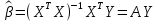 – случайный вектор, его основными числовыми характеристиками являются: – случайный вектор, его основными числовыми характеристиками являются: 1) вектор математических ожиданий Оценка параметра называется несмещенной, если ее математическое ожидание равно значению параметра: 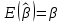 2) автоковариационная матрица: 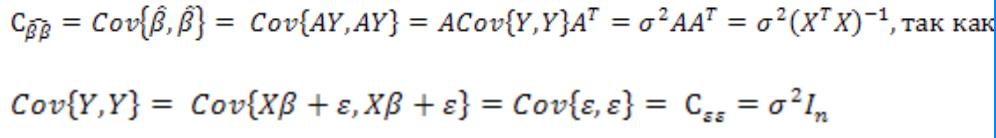 Оценка называется эффективной, если она имеет минимальную среднюю квадратическую ошибку: 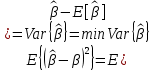 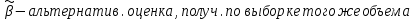 7. Основные числовые характеристики вектора остатков в классической множественной регрессионной модели. 1) Математическое ожидание: 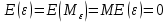 2) Автоковариационная матрица: 8. Основные числовые характеристики вектора возмущений в классической множественной регрессионной модели. 1) Математическое ожидание: E { 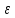 } = 0 } = 02) Автоковариационная матрица: 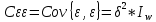 9. Основные числовые характеристики вектора значений эндогенной переменной в классической множественной регрессионной модели. 1) Математическое ожидание: 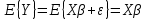 2) Автоковариационная матрица: 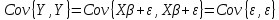 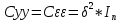 10. Основные числовые характеристики вектора оценок значений эндогенной переменной в классической множественной регрессионной модели. 1) Оценка вектора значений эндогенной переменной: 2) Математическое ожидание: 3) Автоковариационная матрица: 11. Основные числовые характеристики вектора прогнозов значений эндогенной переменной в классической множественной регрессионной модели. 12. Свойство несмещенности МНК- оценок параметров множественной регрессионной модели. Для построения МНК-оценок параметров 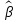 множественной регрессии по выборочным данным используется критерий отбора следующего вида множественной регрессии по выборочным данным используется критерий отбора следующего видагде -вектор столбец остатков множественной регрессии. Выразим ESS через вектор оценок параметров Результат дифференциации критерия ESS по вектору-строке оценок параметра 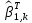 дает необходимое условие экстремума: дает необходимое условие экстремума:Таким образом система нормальных уравнений в матричной форме принимает вид: А вектор-столбец оценок параметров модели определяется линейным выражением Вектор оценок параметров модели - случайный вектор, его основными количественными характеристиками являются: вектор математических ожиданий и матрица автоковариаций. Определим вектор математических ожиданий Таким образом, МНК-оценки параметров множественной регрессии несмещенные, так как мат.ожидание оценки параметра равно истинному значению параметра. 13. Порядок оценивания линейной регрессионной модели в Excel при помощи функции ЛИНЕЙН. Рассмотрим алгоритм оценивания парной линейной регрессии при помощи функции ЛИНЕЙН: 1) В свободном месте рабочего листа выделить область ячеек размером 5 строк и 2 столбца для вывода результатов; 2) В Мастере функций выбрать ЛИНЕЙН (категория «Статистические»); 3) Заполнить поля аргументов функции: Известные_значения_y — адреса ячеек, содержащих значения признака; Известные_значения_x — адреса ячеек, содержащих значения фактора; Константа — значение (логическое), указывающее на наличие свободного члена в уравнении регрессии: если необходимо выполнить оценку двух параметров — постоянного и регрессионного, то в строку Конст следует внести 1; Статистика — значение (логическое), которое указывает на то, следует ли выводить дополнительную информацию по регрессионному анализу или нет: так как при оценке параметров модели нас прежде всего интересуют статистические сведения, в окно строки Статистика следует внести 1; 4) После того, как будут заполнены все аргументы функции, нажать комбинацию клавиш Результаты расчета параметров регрессионной модели:
14. Смысл выходной статистической информации функции ЛИНЕЙН. Функция ЛИНЕЙН специально создана для оценки параметров линейной регрессии, а также для вывода регрессионной статистики. Функция может быть использована как для парной регрессии (прогнозируемая переменная Y зависит от одной контролируемой переменной Х), так и для множественной регрессии (Y зависит от нескольких Х). Рассмотрим результаты вычислений функции ЛИНЕЙН для парной регрессии:
Где , — оценки параметров модели; , — стандартные ошибки оценок параметров; — стандартная ошибка случайного возмущения; — коэффициент детерминации, используемый для определения качества модели, чем лучше качество спецификации, тем значение ближе к 1, чем хуже — тем ближе к 0; — значение статистики, имеющей распределение Фишера и используемой для проверки статистической значимости коэффициента детерминации; — число степеней свободы ( — сумма квадратов остатков (ошибок); — сумма квадратов центрированных по выборочным данным оценок значений эндогенной переменной. 15. Несмещённая оценка дисперсии возмущений регрессионной модели. Несмещенной оценкой дисперсии возмущений множественной регрессии является оценка 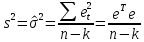 Для доказательства несмещенности данной оценки покажем, что 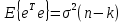 C учетом 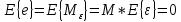 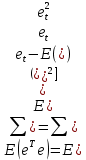 Так как дисперсии остатков 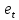 , t =1,2,..,n, являются диагональными элементами автоковариационной матрицы , t =1,2,..,n, являются диагональными элементами автоковариационной матрицы 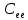 вектора остатков, следовательно, сумма дисперсий – это ее след(следом квадратной матрицы называется сумма ее диагональных элементов): вектора остатков, следовательно, сумма дисперсий – это ее след(следом квадратной матрицы называется сумма ее диагональных элементов):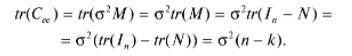 След матрицы N равен: 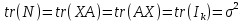 Таким образом, оценка 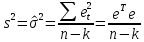 Является несмещенной оценкой дисперсии возмущений: 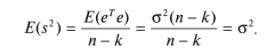 Обозначения: 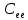 = =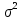 M – автоковариациоонная матрица вектора остатков M – автоковариациоонная матрица вектора остатков 16. Доверительные интервалы параметров парной регрессионной модели. Дробь Стьюдента –нормированная ошибка оценки: распределение Стьюдента, где 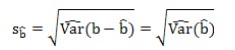 (n-2) – число степеней свободы является параметром распределения Стьюдента. Доверительная вероятность: 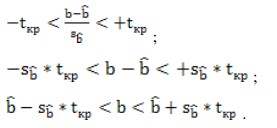 Таким образом, границы доверительного интервала параметра b равны: Аналогично определяются границы доверительного интервала параметра а: |
