Теория Эконометрика. 1. Типы переменных в эконометрических моделях
 Скачать 0.74 Mb.
|
|
17. Проверка значимости оценок параметров линейной регрессионной модели. При проверке качества спецификации парной регрессии наиболее важной является задача установления наличия линейной зависимости между эндогенной переменной и регрессором модели. С этой целью проверяется значимость оценки параметров α и β. В процедуре проверки значимости оценки параметра парной регрессии используется дробь Стьюдента: 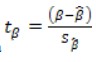 ,которая при истинности гипотезы H0:β = 0, против конкурирующей H1: β 0, принимает вид: 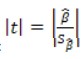 ,и, при выполнении условий Гаусса—Маркова (относительно случайных возмущений), имеет t-распределение с числом степеней свободы n-2. Аналогично формируется t-статистика для проверки гипотезы H0 значимости параметра α, однако параметр β в парной регрессии имеет более важную роль, так как его значимость соответствует значимости регрессора и наличию линейной связи между переменными модели. Алгоритм проверки значимости параметра β выполняется в следующей последовательности: 1) оценка параметров парной регрессии; 2) оценка дисперсии возмущений 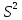 ;3) оценка 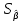 ско оценки параметра β;4) выбор значения tкр (по заданному уровню значимости α и числу степеней свободы (n - 2) из таблиц распределения Стьюдента); 5) проверка неравенства  , при H0: β=0.Если данное неравенство выполняется, то регрессор признается незначимым, если не выполняется, то гипотеза H0: β=0 отвергается и регрессор признается значимым, т. е. между эндогенной переменной и регрессором присутствует линейная зависимость. 18. Интервальная оценка значения зависимой переменной регрессионной модели. 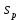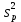Для построения интервальной оценки эндогенной переменной на интервале прогнозирования применяется процедура трансформации дроби Стьюдента  (1)в интервальную оценку:  , (2)где Yp ˆ — прогноз значения эндогенной переменной для момента t = p n , Yp— истинное значение эндогенной переменной на момент t = p ,  — стандартная ошибка прогноза,  — оценка дисперсии ошибки прогноза 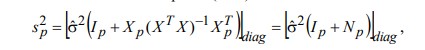 (3)*- diag — диагональный элемент матрицы. Интервальная оценка (2) эндогенной переменной на интервале прогнозирования используется для проверки адекватности эконометрической модели 18 (проверки соответствия результатов прогнозирования, полученных по модели, выборочным данным). 19. Алгоритм проверки адекватности модели. Алгоритм проверки адекватности модели состоит из следующих шагов: 1) результаты наблюдений разделяют на две части: обучающую (90-95% наблюдений) и контролирующую выборки (оставшиеся наблюдения); 2) по обучающей выборке выполняется оценка параметров модели методом наименьших квадратов; 3) по оцененной модели строится прогноз значений эндогенной переменной из контролирующей выборки и доверительные интервалы для их истинных значений; 4) выполняется проверка: если значения эндогенной переменной из контролирующей выборки накрываются доверительным интервалом — модель признается адекватной, в противном случае, подлежит доработке. 20. Коэффициент детерминации регрессионной модели. Квадрат коэффициента корреляции выборки, как правило, обозначается и называется коэффициентом детерминации. Коэффициент детерминации оценивает долю дисперсии (изменчивости) Y, которая объясняется с помощью X в простой линейной регрессионной модели. Итак, пусть мы наблюдаем значения Xi и соответствующие значения Yi , например, доза лекарственного препарата, назначенного пациенту и эффект, доля примеси в меди и проводимость и тд. Выборочный коэффициент корреляции вычисляется по формуле: 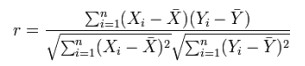 21. Нецентрированный коэффициент детерминации регрессионной модели. Коэффициент детерминации рассматривают, как правило, в качестве основного показателя, отражающего меру качества регрессионной модели, описывающей связь между зависимой и независимыми переменными модели. Коэффициент детерминации показывает, какая доля вариации объясняемой переменной y учтена в модели и обусловлена влиянием на нее факторов, включенных в модель:  где  – значения наблюдаемой переменной,  – среднее значение по наблюдаемым данным,  – модельные значения, построенные по оцененным параметрам.В случае, когда значение константы задается вручную, коэффициент детерминации рассчитывается по следующей формул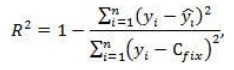е:  где 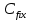 – фиксированное значение константы. В случае линейной регрессии с константой справедлива следующая формула: 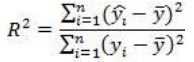 Заметим, что данная формула справедлива только для модели с константой, в общем случае используется предыдущая формула. Чем ближе 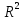 к 1, тем выше качество модели. При равенстве коэффициента единице линия регрессии точно соответствует всем наблюдениям. Равенство коэффициента нулю означает, что выбранные факторы не улучшают качество предсказания по сравнению с тривиальным предсказанием 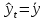 . Достаточно качественной можно признать модель с коэффициентом детерминации выше 0,8. Недостатком коэффициента детерминации является то, что он увеличивается при добавлении новых объясняющих переменных, что необязательно означает улучшение качества регрессионной модели. По этой причине, для устранения этого недостатка, на практике чаще используется скорректированный коэффициент детерминации. Коэффициент детерминации можно получить из функции ЛИНЕЙН: 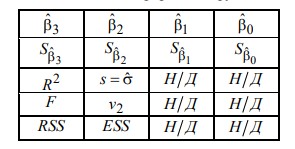 22. Скорректированный коэффициент детерминации модели множественной регрессии. Скорректированный коэффициент детерминации: 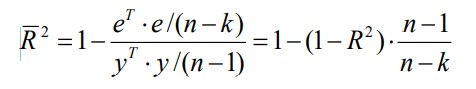 где 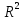– коэффициент детерминации, n – общее число наблюдений, k – число объясняющих переменных (число параметров модели регрессии без учета свободного члена). Скорректированный коэффициент детерминации применяется для решения двух типов задач: оценка тесноты связи между объясняемой и объясняющей переменной. Необходимо обратить внимание на близость к нескорректированному коэффициенту детерминации. Модель считается качественной, если показатели велики и несильно отличаются друг от друга. сравнение моделей с различным числом параметров. При прочих равных условиях, предпочтение отдается той модели, у которой скорректированный коэффициент детерминации больше. Следует отметить, что скорректированный коэффициент детерминации нельзя использовать в формулах, где применяется обычный коэффициент детерминации, поскольку скорректированный коэффициент детерминации нельзя интерпретировать как долю вариации объясняемой переменной, обусловленную вариацией факторов, включенных в модель. 23. F-тест качества спецификации регрессионной модели. Первый шаг. Вычисление статистики с известным распределением 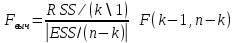 статистика Фишера Второй шаг. Проверка значимости статистики F Проверка гипотезы H0:F=0 Статистика незначима, если 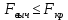 Статистика значима, если 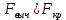 Определение критического значения F - статистики в Excel: Категория — Статистические Функция — Fраспобр; F.обр.ПХ Параметры функции Fраспобр: 1. Вероятность (уровень значимости) 2. Число степеней свободы 1 (v1 =k-1) 3. Число степеней свободы 2 (v2 = n - k) Третий шаг. Установление взаимосвязи между вспомогательной статистикой и коэффициентом детерминации 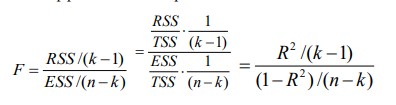 Вывод. Проверка значимости F-статистики позволяет сделать вывод о значимости коэффициента детерминации, так как F= 0 при R^2=0 Если Fвыч Fкр то нулевая гипотеза не отвергается 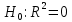 24. Тестирование значимости группы оценок параметров. Для проверки статистической значимости некоторой части (группы) оценок параметров, т.е. о равенстве нулю не всех коэффициентов регрессии одновременно, используется F- статистика вида: 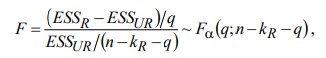 (1)где ESSUR — сумма квадратов остатков «длинной» регрессии, включающей все регрессоры, ESSR — сумма квадратов остатков «короткой» регрессии, включающей регрессоры на параметры которых не наложены ограничения нулевой гипотезы, kR — число параметров короткой регрессии, kUR = kR + q — число параметров длинной регрессии, q = kUR − kR. 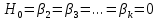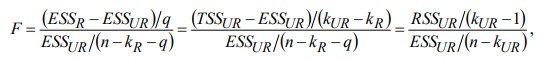В случае, если на параметры всех регрессоров длинной регрессии, кроме свободного члена, наложены ограничения в рамках нулевой гипотезы  статистика (1) принимает вид  С учетом того, что 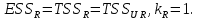 25. Тестирование правильности составления спецификации: тест Рамсея. Типичными ошибками спецификации модели являются следующие: Неверно выбран тип уравнения регрессии (например, вместо нелинейной функции использовалась линейная) В линейное уравнение множественной регрессии включен несущественный регрессор В линейное уравнение множественной регрессии не включен существенный регрессор Для тестирования правильности выбора спецификации в эконометрических пакетах применяется тест RESET, предложенный Рамсеем в 1969 г. Алгоритм теста состоит из следующих шагов. 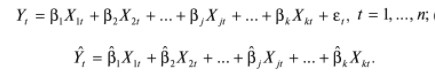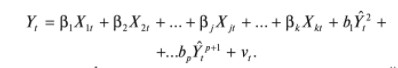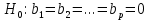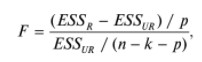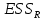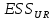Оценивается спецификация исследуемой модели:  Оценивается вспомогательная регрессия:  Нулевая гипотеза формулируется в рамках вспомогательной модели:  Нулевую гипотезу можно проверить при помощи F-теста:  (1)Где  - сумма квадратов остатков усеченной (исследуемой) регрессии;  - сумма квадратов остатков неусеченной (вспомогательной) регрессии.Если вычисленное значение статистики окажется больше критического значения  Гипотеза 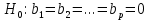отвергается, и спецификация модели признается неверной. F-статистики типа (1) имеют распределение Фишера только в случае, если случайные возмущения регрессионной модели являются независимыми и нормально распределенными. 26. Диагностика эконометрических моделей: тестирование гипотезы нормальности возмущений (тест Харке-Бера). Одним из часто используемых тестов на нормальность случайных возмущений регрессионных моделей является тест Харке-Бера. Статистика теста основана на сравнении центральных нормированных моментов третьего (коэффициент ассиметрии)  и четвертого (коэффициент островершинности)  порядков случайных возмущений исследуемой модели с соответствующими характеристиками нормального распределения, для которого, как известно, S=0, K=3 и имеет вид  (1)Оценки характеристик, включенных в формулу, вычисляются через остатки регрессионной модели:  Где -  оценка дисперсии возмущений, полученная в рамках метода максимального правдоподобия. Нулевая и альтернативные гипотезы теста Харке-Бера формулируются следующим образом:  Статистика (1) имеет распределение хи-квадрат с двумя степенями свободы, и если вычисленное значение больше критического, нулевая гипотеза о нормальном распределении возмущений регрессионной модели отвергается. Тест Харке-Бера является асимптотическим тестом, те применим к большим выборкам. Для малых выборок в эконометрических пакетах в формуле (1) сомножитель перед скобками заменен на n-k:  Где k- число оцениваемых параметров регрессионной модели. 27. Автокорреляция случайного возмущения: причины, последствия. Автоковариационная матрица вектора случайных возмущений при наличии автокорреляции имеет следующую структуру:  Причинами автокорреляции являются: Ошибки спецификации (пропуск важной объясняющей переменной, использование ошибочной функциональной зависимости между переменными) Ошибки измерений Характер наблюдений (например, данные временных рядов) Последствия автокорреляции такие же, как и от гетероскедастичности. Вектор остатков регрессии  при наличии автокорреляции возмущений имеет количественные характеристики В этом случае  Что приводит к нарушению свойства несмещенности оценок дисперсии возмущения и автоковариационных матриц всех случайных векторов эконометрической модели. 28. Алгоритм теста Дарбина-Уотсона на наличие (отсутствие) автокорреляции случайных возмущений. Тест Дарбина-Уотсона основан на предпосылках: случайное возмущение  распределено нормально и не подвержено гетероскедастичности, модель не включает лаговые значения эндогенных переменных. Статистика теста вычисляется по формуле: Где е- остатки регрессии,  - выборочный коэффициент корреляции между остатками регрессии, разделенными одним лагом.Против нулевой гипотезы теста  можно выбрать три альтернативные:  (двусторонный тест)  (односторонний тест),  (односторонний тест).Последовательность его выполнения: 1. выполняется оценка параметров модели и вычисление остатков:  , где 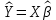 2. вычисление статистики DW (по формуле выше): 3.выбор табличных значений границ критического значения статистики: du, dL( по параметрам n, K=k-1, α- для одностороннего теста, а/2 – для двустороннего теста); 4.определение интервала, в который попадает вычисленное значение статистики DW.  При этом возможны следующие случаи: Наличие положительной автокорреляции: DW Наличие отрицательной автокорреляции: DW >4-dL. Автокорреляция отсутствует: dU≤ DW≤ 4-dU. Зоны неопределенности: dL Поскольку коэффициент корреляции принимает значения -1<=r<=1 то для значений статистики DW выполняется неравенство 0<=DW<=4. |