29. Способы корректировки автокорреляции: алгоритм метода Кохрейна-Оркатта.
Пусть исходное уравнение регрессии 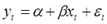 содержит автокорреляцию случайных членов. содержит автокорреляцию случайных членов.
Допустим, что автокорреляция подчиняется автокорреляционной схеме первого порядка: 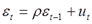 , где , где 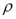 - коэффициент автокорреляции, а - коэффициент автокорреляции, а 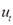 - случайный член, удовлетворяющий предпосылкам МНК. - случайный член, удовлетворяющий предпосылкам МНК.
Данная схема оказывается авторегрессионой, поскольку 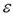 определяется значениями этой же величины с запаздыванием, и схемой первого порядка, потому что в этом случае запаздывание равно единице. определяется значениями этой же величины с запаздыванием, и схемой первого порядка, потому что в этом случае запаздывание равно единице.
Величина  есть коэффициент корреляции между двумя соседними ошибками. Пусть есть коэффициент корреляции между двумя соседними ошибками. Пусть 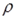 известно. Преобразуем исходное уравнение регрессии следующим образом: известно. Преобразуем исходное уравнение регрессии следующим образом:
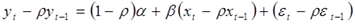 . .
Алгоритм метода Кохрейна-Оркатта.
1. По выборочным данным выполняется настройка модели, и вычисляется вектор остатков регрессии е = (e1, e2 , …, en)T.
2. По остаткам регрессии оценивается модель авторегрессии et=ρet-1+ vt
3. С оценкой параметра авторегрессии выполняются этап преобразования переменных и определения МНК – оценок вектора параметра β.
4. Строится новый вектор остатков, и процедура повторяется, начиная с п. 2. Интеграционный процесс заканчивается при условии совпадения оценок по последней и предпоследней интерациях с заданной степенью точности.
30. Гетероскедастичность случайного возмущения: причины, последствия.
Гетероскедастичность - ситуация, когда дисперсия ошибки в уравнении регрессии изменяется от наблюдения к наблюдению. В этом случае приходится подвергать определенной модификации МНК (иначе возможны ошибочные выводы). Для обнаружения гетероскедастичности обычно используют 3 теста: тест ранговой корреляции Спирмена, тест Голдфеда-Квандта и тест Глейзера Доугерти.
Гетероскедастичность случайных возмущений – возмущения обладают различными дисперсиями r2i=r2wi, но не коррелированны друг с другом.
Причина: при гетероскедастичности распределение u для каждого наблюдения имеет нормальное распределение и нулевое ожидание, но дисперсия распределений различна.
Последствия нарушения условия гомоскедастичности случайных возмущений:
1. Потеря эффективности оценок коэффициентов регрессии, т.е. можно найти другие, отличные от Метода Наименьших Квадратов и более эффективные оценки
2. Смещенность стандартных ошибок коэффициентов в связи с некорректностью процедур их оценки
31. Алгоритм теста Голдфельда-Квандта на наличие (отсутствие) гетероскедастичности случайных возмущений.
Гипотеза(1): 
Шаг 1. Уравнения наблюдений объекта следует упорядочить по возрастанию суммы модулей значений предопределенных переменных модели (2),
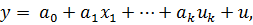
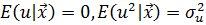
т.е. по возрастанию значений

Шаг 2. По первым упорядоченным уравнениям наблюдений объекта вычислить МНК-оценки параметров модели и величину 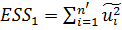 где где 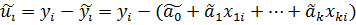 - МНК-оценка случайного возмущения - МНК-оценка случайного возмущения
Шаг 3. По последним упорядоченным уравнениям наблюдений вычислить МНК-оценки параметров модели и величину ESS, которую обозначим
Шаг 4.Вычислить статистику 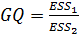 . .
Шаг 5. Задаться уровнем значимости и с помощью функции FРАСПОБР Excel при количествах степеней свободы , где 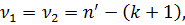 определить (1- -квантиль, определить (1- -квантиль, 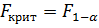 распределения Фишера. распределения Фишера.
Шаг 6. Принять гипотезу (1), если справедливы неравенства
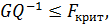
Т.е. при справедливых неравенствах случайный остаток в модели (2) полагать гомоскедастичными. В противном случае гипотезу (1) отклонить как противоречащую реальным данным и сделать вывод о гетероскедастичности случайного остатка в модели (2).
32. Способы корректировки гетероскедастичности. Метод взвешенных наименьших квадратов.
Одним из основных способов корректировки гетероскедастичности является использование метода взвешенных наименьших квадратов. Он применяется в том случае, когда известны диагональные элементы автоковариационной матрицы вектора возмущений 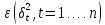 . В этом случае уравнения наблюдений можно преобразовать следующим образом. Поделим каждый член на СКО возмущения: . В этом случае уравнения наблюдений можно преобразовать следующим образом. Поделим каждый член на СКО возмущения:  , где t=1….n. В результате преобразования спецификация принимает вид спецификации классической регрессионной модели: , где t=1….n. В результате преобразования спецификация принимает вид спецификации классической регрессионной модели: 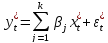 . Определим количественные характеристики случайного возмущения : . Определим количественные характеристики случайного возмущения :
математическое ожидание: E{ }=E{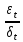 }= }=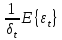 =0 =0
дисперсия случайного члена: Var { }=Var{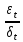 }= }=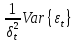 = =1, таким образом = =1, таким образом
N(0,1) и при помощи данного преобразования случайное возмущение приобрело свойство гомоскедастичности.
В случае, если значения 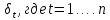 неизвестны, используется доступный обобщенный метод наименьших квадратов. В этом методе выполняется оценка неизвестных дисперсий, но при условии, что на структуру автоковариационной матрицы накладываются дополнительные ограничения (предпосылки). Наиболее часто используется следующая предпосылка: СКО возмущения пропорционально одному из регрессоров. неизвестны, используется доступный обобщенный метод наименьших квадратов. В этом методе выполняется оценка неизвестных дисперсий, но при условии, что на структуру автоковариационной матрицы накладываются дополнительные ограничения (предпосылки). Наиболее часто используется следующая предпосылка: СКО возмущения пропорционально одному из регрессоров.
33. Способы корректировки гетероскедастичности. Доступный метод взвешенных наименьших квадратов.
34. Мультиколлинеарность в моделях множественной регрессии. Полная мультиколлинеарность: определение, последствия, способы устранения.
35. Мультиколлинеарность в моделях множественной регрессии. Частичная мультиколлинеарность: определение, признаки, последствия, способы устранения.
36. Спецификация и оценивание МНК эконометрических моделей нелинейных по параметрам, интерпретация параметров.
37. Способы включения случайных возмущений в спецификацию нелинейной по параметрам модели.
38. Спецификация и оценивание МНК эконометрических моделей нелинейных по переменным.
39. Фиктивная переменная сдвига: спецификация регрессионной модели с фиктивной переменной сдвига, смысл параметра при фиктивной переменной.
40. Применение фиктивных переменных сдвига при исследовании сезонных колебаний: спецификация модели; проблема мультиколлинеарности; смысл параметров при фиктивных переменных.
Термин “фиктивные переменные” используется как противоположность “значащим” переменным, показывающим уровень количественного показателя, принимающего значения из непрерывного интервала. Как правило, фиктивная переменная — это индикаторная переменная, отражающая качественную характеристику. Чаще всего применяются бинарные фиктивные переменные, принимающие два значения, 0 и 1, в зависимости от определенного условия. Например, в результате опроса группы людей 0 может означать, что опрашиваемый - мужчина, а 1 - женщина. Могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, принадлежность к определенному региону.
Регрессионная модель, включающая в качестве фактора (факторов) фиктивную переменную, называется регрессионной моделью с переменной структурой.
Рассмотрим временной ряд Xi j,
где i — это номер сезона (периода времени внутри года, напри мер, месяца или квартала);
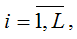 (L — число сезонов в году); (L — число сезонов в году);
j — номер года, j = (m — общее количество лет).
Количество уровней исходного ряда равно L × m = n. Число сезонных фиктивных переменных в регрессионной модели всегда должно быть на единицу меньше сезонов внутри года, т. е. должно быть равно величине L − 1. При моделировании годовых данных регрессионная модель, помимо фактора времени, должна содержать одиннадцать фиктивных компонент (12 − 1).
Каждому из сезонов соответствует определенное сочетание фиктивных переменных. Сезон, для которого значения всех фиктивных переменных равны нулю, принимается за базу сравнения. Для остальных сезонов одна из фиктивных переменных принимает значение, равное единице. Если имеются поквартальные данные, то значения фиктивных переменныхD1, D2, D3 будут принимать следующие значения для каждого из кварталов
Квартал
|
D2
|
D3
|
D4
|
1
|
0
|
0
|
0
|
2
|
1
|
0
|
0
|
3
|
0
|
1
|
0
|
4
|
0
|
0
|
1
|
Общий вид регрессионной модели с переменной структурой в данном случае будет иметь вид:
yt =β0 +β1 ×t+δ2 ×D2 +δ3 ×D3 +δ4 ×D4 +εt
Построенная модель регрессии является разновидностью аддитивной модели временного ряда. Базисным уравнением исследуемой регрессионной зависимости будет являться уравнение тренда для первого квартала:
y =β +β ×t+ε
Тогда общий вид модели регрессии с переменной структурой будет иметь вид:
yt=β0+ β1*t+δ2*D2+δ3*D3+δ4*D4+εt.
Данная модель регрессии представляет собой одну из разновидностей аддитивной модели временного ряда.
На основе общей модели регрессии с переменной структурой можно составить базисную модель или модель тренда для первого квартала:
yt=β0+ β1*t+εt.
Также на основе общей модели регрессии с переменной структурой можно составить частные модели регрессии:
1) частная модель регрессии для второго квартала:
yt=β0+ β1*t+δ2+εt;
2) частная модель регрессии для третьего квартала:
yt=β0+ β1*t+δ3+εt;
3) частная модель регрессии для четвёртого квартала:
yt=β0+ β1*t+δ4+εt.
Данные частные модели регрессии отличаются друг от друга только на величину свободного члена δi.
Коэффициент β1 характеризует среднее абсолютное изменение уровней временного ряда под влиянием основной тенденции.
Сезонная компонента для каждого сезона рассчитывается как разность между средним значением свободных членов всех частных моделей регрессий и значением постоянного члена одной из моделей.
Среднее значение свободных членов всех частных моделей регрессий рассчитывается по формуле:
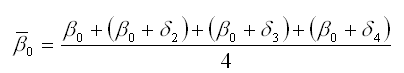
Для поквартальных данных оценка сезонных отклонений осуществляется по формулам:
1) оценка сезонного отклонения для первого квартала:
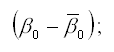
2) оценка сезонного отклонения для второго квартала:
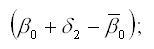
3) оценка сезонного отклонения для третьего квартала:
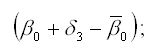
4) оценка сезонного отклонения для четвёртого квартала:
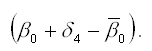
Сумма сезонных отклонений должна равняться нулю.
41. Фиктивная переменная наклона: назначение; спецификация регрессионной модели.
Фиктивные (искусственные) переменные (dummy variables)- это переменные с дискретным множеством значений, которые количественным образом описывают качественные признаки.
В регрессионных моделях применяются фиктивные переменные двух типов: переменные сдвига и переменные наклона.
Фиктивная переменная наклона изменяет наклон линии регрессии. При помощи фиктивных переменных наклона можно построить кусочно-линейные модели, которые позволяют учесть структурные изменения в экономических процессах (например, введение новых правовых или налоговых ограничений, изменение политической ситуации и т. д.).
Спецификация регрессионной модели в этом случае (например, для парной регрессионной модели, для простоты) имеет вид:
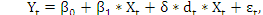
0 – до структурных изменений
dt = 1 – после структурных изменений,
dt - бинарная переменная
Фиктивная переменная входит в уравнение в мультипликативной форме.
42. Тест Чоу на значимость структурных изменений.
43. Классификация динамических регрессионных моделей.
44. Спецификация и оценка моделей с распределенными лагами с конечным числом лагов (метод замены).
45. Характеристики лаговой структуры: краткосрочный мультипликатор, долгосрочный мультипликатор, относительные параметры, средний лаг.
46. Спецификация и оценка моделей с распределенными лагами с бесконечным числом лагов: метод геометрической прогрессии.
47. Оценка моделей с распределенными лагами: метод Алмон.
48. Тест Дарбина на наличие (отсутствие) автокорреляции вектора возмущений в авторегрессионных моделях.
49. Системы одновременных уравнений (СОУ): проблема оценивания структурных параметров.
50. Идентификация отдельных уравнений системы одновременных уравнений: порядковое условие.
51. Идентификация отдельных уравнений системы одновременных уравнений: ранговое условие.
52. Косвенный метод наименьших квадратов: условие применения, алгоритм метода.
53. Двухшаговый метод наименьших квадратов (ДМНК): условие применения, алгоритм метода.
54. Корректировка оценки дисперсии возмущения и стандартных ошибок оценок параметров при реализации алгоритма ДМНК в Excel.
Рекомендуемая литература
1. Бабешко Л.О. Основы эконометрического моделирования: Учебное пособие. - М.: КомКнига, 2015.
2. Бабешко Л.О. Эконометрика и эконометрическое моделирование: учебник [Текст] / Л.О. Бабешко, М.Г. Бич, И.В. Орлова. — М.: Вузовский учебник: ИНФРА-М, 2017.
3.Бывшев В.А. Эконометрика: Учебное пособие. – М: «Финансы и статистика», 2008.
4. Доугерти К. Введение в эконометрику : учеб.; пер. с англ.— 3-е изд. — М.: ИНФРА-М, 2010 .— 465 с.
5. Елисеева И.И. Эконометрика. — М.: Юрайт, 2012. — 453 с.
6. Кремер Н.Ш. Эконометрика: учебник.— 3-е изд. / перераб. и доп. — М.: ЮНИТИ, 2010 .— 328с.
7. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика: Начальный курс: - М.: Дело, 2007.
8. William H. Greene Econometric analysis. Pearson International Edition, New Jersey, 2008 |
 Скачать 0.74 Mb.
Скачать 0.74 Mb.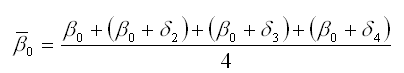
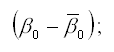
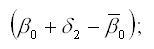
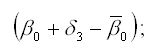
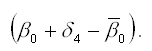

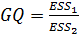 .
. , где t=1….n. В результате преобразования спецификация принимает вид спецификации классической регрессионной модели:
, где t=1….n. В результате преобразования спецификация принимает вид спецификации классической регрессионной модели: 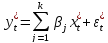 . Определим количественные характеристики случайного возмущения :
. Определим количественные характеристики случайного возмущения :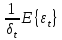 =0
=0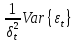 = =1, таким образом
= =1, таким образом