1 вопрос. Динамика точки. Основные понятия и определения
 Скачать 1.54 Mb. Скачать 1.54 Mb.
|
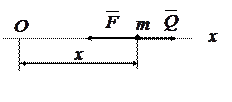 Спроектировав его на ось , получаем дифференциальное уравнение движения точки: где , Здесь 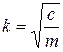 частота свободных колебаний; и имеет размерность ускорения. частота свободных колебаний; и имеет размерность ускорения.Уравнение — дифференциальное уравнение вынужденных колебаний точки при отсутствии сопротивления. Решение этого уравнения зависит от соотношения между частотой возмущающей силы и частотой собственных колебаний. Тут возможны два случая: 1) и 2) . 1. Случай отсутствия резонанса. Найдем решение уравнения (2.23) для случая, когда частота возмущающей силы отлична от частоты свободных колебаний ( —нет резонанса.). Уравнение (2.23)—неоднородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его решение складывается из общего решения однородного уравнения и частного решения данного уравнения (2.23): Однородное уравнение совпадает с дифференциальным уравнением собственных колебаний (2.2) и его решение может быть записано в двух эквивалентных формах (2.3) и (2.6): Частное решение неоднородного уравнения (2.23) определяется правой частью этого уравнения. В случае будем искать это решение в виде: Постоянную следует определить из условия, что функция —частное решение уравнения (2.23) и, кроме того, подстановка в это уравнение должна превратить его в тождество. Вычисляем необходимые производные по времени от : После подстановки в (2.23) получаем: Полученное равенство будет выполняться при любом значении , если откуда 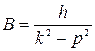 . .Подставляя найденное значение в (2.25), находим искомое частное решение неоднородного уравнения: 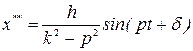 . .Общее решение уравнения (2.23) имеет окончательный вид 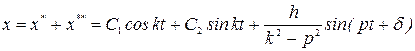 . .В амплитудной форме 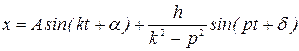 . .Решение (2.29) показывает, что колебания в рассматриваемом случае слагаются из: 1) колебаний с амплитудой и частотой , называемых собственными колебаниями; 2) колебаний с амплитудой и частотой , которые называются вынужденными колебаниями. Постоянные интегрирования и , или и определяются по начальным условиям: , . Предварительно найдем 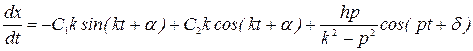 . .Подставляя эти значения в выражения для и при , получаем 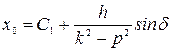 , , 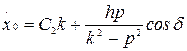 . .Отсюда 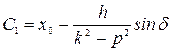 , , 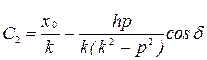 . .Амплитуда собственных колебаний и начальная фаза через и выражается формулами , 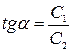 Следовательно, амплитуда и начальная фаза собственных колебаний при действии возмущающей силы зависят не только от начальных условий, но и от параметров этой силы, то есть собственные колебания в этом случае могут возникнуть не только из-за начальных условий, но и благодаря действию возмущающей силы даже при нулевых начальных условиях. Рассмотрим вынужденные колебания, определяемые формулой 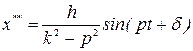 Частота этих колебаний, как видно, равна частоте возмущающей силы, амплитуда 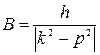 . .В зависимости от соотношения между частотами вынужденные колебания можно выразить в двух формах: при при Следовательно, при фаза вынужденных колебаний совпадает с фазой возмущающей силы. В этом случае сдвиг фаз между ними равен нулю, то есть вынужденные колебания и возмущающая сила достигают одновременно максимальных и минимальных значений. При сдвиг фаз . Действительно, сдвиг фаз как разность фаз между возмущающей силой и вынужденными колебаниями В этом случае вынужденные колебания находятся в противофазе по отношению к возмущающей силе, то есть, в частности, если возмущающая сила достигает максимума, то функция достигает минимума и наоборот. Итак, вынужденные колебания системы без сопротивления при , возбуждаемые гармонической возмущающей силой: 1) являются гармоническими колебаниями с постоянной амплитудой; 2) их частоты совпадают с частотой возмущающей силы; 3) они не зависят от начальных условий. 2. Случай резонанса. Резонансом называется случай совпадения частот собственных колебаний и возмущающей силы, т. е.когда . Как и в предыдущем случае, дифференциальное уравнение движения определяется уравнением и оно имеет общее решение . Здесь общее решение однородного уравнения по-прежнему имеет вид А вот частное решение неоднородного уравнения будем искать в виде -рассматривается случай . Постоянная определяется из условия, что при подстановке в рассматриваемое неоднородное дифференциальное уравнение это уравнение обращается в тождество. Вычисляем производные: и подставляем значения и в уравнение : или Приравнивая коэффициенты при синусе в левой и правой частях этого уравнения: 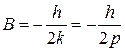 . . Получаем, что частное решение 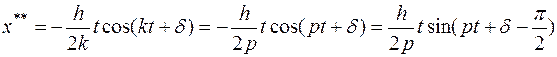 , ,а искомое общее решение уравнения 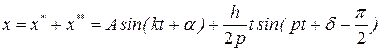 . .Уравнение показывает, что движение точки при резонансе является результатом наложения свободных и вынужденных колебаний точки, так же, как и при . Рассмотрим вынужденные колебания при резонансе Основной особенностью этих колебаний является зависимость их амплитуды от времени 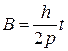 . .Амплитуда вынужденных колебаний при резонансе увеличивается пропорционально времени. Частота и период вынужденных колебаний при резонансе равны частоте и периоду свободных колебаний точки. Фаза вынужденных колебаний отстает от фазы возмущающей силы величину |
