1 вопрос. Динамика точки. Основные понятия и определения

Название	1 вопрос. Динамика точки. Основные понятия и определения
Дата	19.06.2018
Размер	1.54 Mb.
Формат файла
Имя файла	teor_mekh_ekz.docx
Тип	Документы #47317
страница	9 из 11

1 2 3 4 5 6 7 8 9 10 11

35-42 вопрос ._{Обобщенные координаты .Число степеней свободы. Возможные и виртуальные перемещения точки и системы.}

_{Принцип возможных перемещений}_{: для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении была равна нулю.}_{или в проекциях:}

_.

_{Принцип возможных перемещений дает в общей форме условия равновесия для любой механической системы, дает общий метод решения задач статики.}

_{Если система имеет несколько степеней свободы, то уравнение принципа возможных перемещений составляют для каждого из независимого перемещений в отдельности, т.е. будет столько уравнений, сколько система имеет степеней свободы.}

_{Принцип возможных перемещений удобен тем, что при рассмотрении системы с идеальными связями их реакции не учитываются и необходимо оперировать только активными силами.}

_{Принцип возможных перемещений формулируется следующим образом:}

_{Для того, чтобы матер. система, подчиненная идеальным связям находилась в состоянии покоя, необходимо и достаточно, чтобы сумма элементарных работ, производимых активными силами на возможных перемещениях точек системы была положительная.}

_{Общее уравнение динамики}_{– при движении системы с идеальными связями в каждый данный момент времен сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы будет равна нулю. Уравнение использует принцип возможных перемещений и принцип Даламбера и позволяет составить дифференциальные уравнения движения любой механической системы. Дает общий метод решения задач динамики. Последовательность составления: а) к каждому телу прикладывают действующие на него задаваемые силы, а также условно прикладывают силы и моменты пар сил инерции; б) сообщают системе возможные перемещения; в) составляют уравнения принципа возможных перемещений, считая систему находящейся в равновесии.}

_{Следует отметить, что общее уравнение динамики можно применять и для систем с неидеальными связями, только в этом случае реакции неидеальных связей, таких, например, как сила трения или момент трения качения, необходимо отнести к категории активных сил.}

_{Работа на возможном перемещении как активных, так и сил инерций, ищется также как и элементарная работа на действительном перемещении:}

_{Возможная работа силы:}

_.

_{Возможная работа момента (пары сил):}

_.

_{4. Обобщенными координатами механической системы называются независимые между собой параметры q1, q2, …, qS}_{любой размерности, однозначно определяющие положение системы в любой момент времени.}

_{Число обобщенных координат равно}_S_{– числу степеней свободы механической системы. Положение каждой ν-й точки системы, то есть ее радиус вектор в общем случае всегда можно выразить в виде функции обобщенных координат:}

₍₂₄₎

_{Общее уравнение динамики в обобщенных координатах выглядит в виде системы S уравнений следующим образом:}

_;

_{……..………. ;}

₍₂₅₎

_{………..……. ;}

_,

_здесь_{– обобщенная сила, соответствующая обобщенной координате}_:

₍₂₆₎

_а_{– обобщенная сила инерции, соответствующая обобщенной координате}_:

_{Число независимых между собою возможных перемещений системы называется числом степеней свободы этой системы.}_{Например. шар на плоскости может перемещаться в любом направлении, но любое его возможное перемещение может быть получено как геометрическая сумма двух перемещений вдоль двух взаимно перпендикулярных осей. Свободное твердое тело имеет 6 степеней свободы.}_{Обобщенные силы.}_{Каждой обобщенной координате}_{можно вычислить соответствующую ей обобщенную силу}_Qk_{.Вычисление производится по такому правилу.}

_{Чтобы определить обобщенную силу}_Qk_{, соответствующую обобщенной координате}_qk_{, надо дать этой координате приращение}_{(увеличить координату на эту величину), оставив все другие координаты неизменными, вычислить сумму работ всех сил, приложенных к системе, на соответствующих перемещениях точек и поделить ее на приращение координаты}_:

₍₇₎

_{где –}_{перемещение}_i_{-той точки системы, полученное за счет изменения}_k_{–той обобщенной координаты.}

_{Обобщенная сила определяется с помощью элементарных работ. Поэтому эту силу можно вычислить иначе:}

_{И так как}_{есть приращение радиуса-вектора}_{за счет приращения координаты}_{при остальных неизменных координатах и времени}_t_{, отношение}_{можно определять как частную производную}_{. Тогда}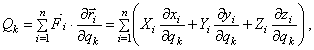

₍₈₎

_{где координаты точек – функции обобщенных координат (5).}

_{Если система консервативная, то есть движение происходит под действием сил потенциального поля, проекции которых}_{, где}_{, а координаты точек – функции обобщенных координат, то}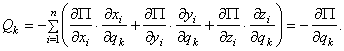

₍₉₎

_{Обобщенная сила консервативной системы есть частная производная от потенциальной энергии по соответствующей обобщенной координате со знаком минус.}

_{Конечно, при вычислении этой обобщенной силы потенциальную энергию следует определять как функцию обобщенных координат}

_{П = П(}_q_1,_q_2,_q_3,…,_qs_{). Замечания:}

_{Первое. При вычислении обобщенных сил реакции идеальных связей не учитываются.}

_{Второе. Размерность обобщенной силы зависит от размерности обобщенной координаты.}

_{Уравнения Лагранжа 2-го рода}_{выводятся из общего уравнения динамики в обобщенных координатах. Число уравнений соответствует числу степеней свободы:}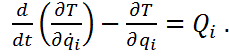

₍₂₈₎

_{Для составления уравнения Лагранжа 2-го рода выбираются обобщенные координаты}_{и находятся обобщенные скорости}_._{Находится кинетическая энергия системы, которая является функцией обобщенных скоростей}_,_{и, в некоторых случаях, обобщенных координат. Выполняются операции дифференцирования кинетической энергии, предусмотренные левыми частями уравнений Лагранжа.Полученные выражения приравниваются обобщенным силам, для нахождения которых помимо формул (26) часто при решении задач используют следующие:}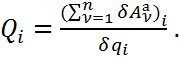

₍₂₉₎

_{В числителе правой части формулы – сумма элементарных работ все активных сил на возможном перемещении системы, соответствующем вариации i-й обобщенной координаты –}_{. При этом возможном перемещении все остальные обобщенные координаты не изменяются. Полученные уравнения являются дифференциальными уравнениями движения механической системы с}_S_{степенями свободы.}

_{……………………………………………………………………………………………………………………………….}

_{43 ,44вопрос.}_{Понятие о силовом поле. Потенциальное силовое поле и силовая функция.}

_{Силовым полем}_{называется часть пространства, в котором на материальную точку действует сила, зависящая от координат точки и времени}

_{Если сила явно не зависит от времени, то силовое поле называется}_{стационарным}_.

_{Стационарное силовое поле называется потенциальным, если проекции силы}_{на оси}_{Ох, Оу, Oz}_{можно выразить через скалярную функцию}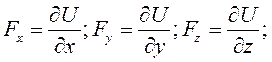

_{по формулам}

_(I)

_т.е.

_{Функция}

_{называется силовой функцией. Из (I) следует, что силовая ф-я}_U_{определяется с точностью до аддитивной постоянной.}

_{Потенциальной энергией материальной точки в данной точке потенциального силового поля называют работу, производимую силой, действующей на точку в потенциальном силовом поле, при её перемещении из рассматриваемой точки поля}_{в начальную}_{., условно принимаемую за нулевую}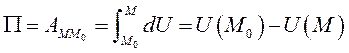

_{……………….……………………………………………………………………………………………………………………}

_{45вопрос .Поверхность уровня и их свойства.}

_{Поверхность}

_{на которой силовая функция U имеет постоянное значение, называется}_{эквипотенциальной поверхностью}_или_{поверхностью уровня}_.

_{1. Если начальная и конечная точки расположены на одной и той же поверхности уровня, то работа силы стационарного потенциального по перемещению материальной точки из начального положения в конечное равна нулю.}

_т.к.

_{2. Сила}_{потенциального поля направлена по нормали к поверхности уровня в сторону возрастания силовой функции}_U_.

_{……………………………………………………………………………………………………………………………}

_{46 вопрос}_{Устойчивость положения равновесия механической системы. Теорема Лагранжа-Дирихле.}

_{Рассмотрим механическую систему с голономными, стационарными и неосвобождающими связями с n степенями свободы, движение которой определяется обобщенными координатами q1, q2, .., qn.}

_{В соответствии с принципом возможных перемещений в положении равновесия все обобщенные силы равны нулю: Q1=0, .., Qn=0.}

_{Для консервативной системы эти условия принимают вид:}

_{(19.1)

где П — потенциальная энергия системы.}

_{Поскольку П есть П(q1, q2, .., qn), (19.1) можно рассматривать как систему уравнений относительно обобщенных координат, представляющих собой условия экстремума потенциальной энергии. Решая их можно найти положения, в которых система будет находиться в равновесии.}

_Однако_{положение равновесия}_{может быть}_{устойчивым, неустойчивым и безразличным}_.

_{Если существует такое достаточно малое отклонение системы от положения равновесия, при котором она стремится вернуться назад, то такое положение равновесия будет}_{устойчивым}_{. В случае, когда при любом начальном отклонении система удаляется от положения равновесия, положение равновесия будет}_{неустойчивым}_{. Если же при начальном отклонении система остается в отклоненном положении, то положение равновесия будет}_{безразличным}_.

_{На рис. 19.1 представлены устойчивое (см. рис. 19.1, а) и неустойчивое (см. рис. 19.1, б) положения равновесия математического маятника. Безразличное положение равновесия имеет система, приведенная на рис. 19.1, в.}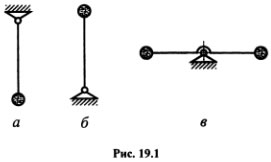

http://extm10.narod2.ru/sem4/ev/11_2.jpg

_{При устойчивом положении равновесия система после достаточно малого начального возмущения совершает колебания около положения равновесия или возвращается в это положение без колебаний. При неустойчивом положении равновесия система после любого начального возмущения при дальнейшем движении все более удаляется от положения равновесия.}

_{Строгое определение понятия устойчивости положения равновесия было дано в конце XIX в. А. М. Ляпуновым. Условимся отсчитывать обобщенные координаты q1, q2, .., qn}_{от положения равновесия, т.е. считать их в положении равновесия равными нулю. Выведем систему из положения равновесия, сообщив обобщенным координатам в начальный момент времени возмущения (отклонения q10, q20, .., qn0, и скорости}

_{). Обозначим обобщенные координаты и их скорости при дальнейшем движении через}

_{соответственно.}

_{По Ляпунову, равновесие системы называется устойчивым, если для любых сколь угодно малых положительных чисел}

_{можно выбрать 2n других таких положительных чисел}

_{что при начальных возмущениях системы, удовлетворяющих условиям}

_{, при дальнейшем движении системы будут выполняться неравенства}

_.

_{В противном случае равновесие будет неустойчивым. Безразличное положение равновесия в соответствии с данным определением относится к неустойчивым, поскольку при наличии начальной скорости система будет удаляться от начального положения.}

_{Если при устойчивом положении равновесия все обобщенные координаты и скорости с течением времени стремятся к нулю:}

_{, то рассматриваемое положение равновесия называется}

1 2 3 4 5 6 7 8 9 10 11