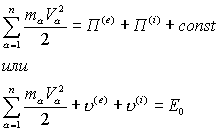1 вопрос. Динамика точки. Основные понятия и определения

Название	1 вопрос. Динамика точки. Основные понятия и определения
Дата	19.06.2018
Размер	1.54 Mb.
Формат файла
Имя файла	teor_mekh_ekz.docx
Тип	Документы #47317
страница	3 из 11

1 2 3 4 5 6 7 8 9 10 11

_{14 вопрос.}_{Классификация сил, действующих на механическую систему: силы внешние и внутренние, активные и реакции связей.}

_{2)Физический маятник. Опытное определение моментов инерции тел.}

_{1)Внешние силы}_{- силы, действующие на материальную точку системы со стороны тел не входящих в состав данной механической системы.}

_{Внутренние силы}_{- силы, действующие между материальными точками данной механической системы.}

_{Силы заданные по условию задачи принято называть-}_{активными силами}_{. А силы, обусловленные наличием связи-}_{реакциями связи.}

₂₎_{Физический маятник}_{- твёрдое тело, совершающее колебания вокруг горизонтальной неподвижной оси под действием только силы тяжести. Ось вращения физического маятника называется-}_{осью привеса}_{. Обозначим φ угол между вертикальной осью, проходящей через ось привеса линией, проходящей перпендикулярно оси привеса через центр тяжести точку С.G- вес тела. Дифференциальное уравнение физического маятника}

_{знак «-» в правой части поставлен потому, что при повороте маятника в положительном направлении (т.е. против часовой стрелки) сила тяжести хочет повернуть маятник в обратном направлении.}

_{- это уравнение называется дифференциальным уравнением колебаний физического маятника.}

_{………………………………………………………………………………………………………………………………………..}

_{15 вопрос.}_{Динамика твердого тела}

_{Механической системой материальных точек или тел называется такая их совокупность, в которой положение и движение каждой точки (или тела) зависит от положения и движения остальных.}

_{Материальное тело рассматривается, как система материальных точек (частиц), которые образуют это тело.}

_{Классификация сил, действующих на механическую систему:}

_{Внешними}_{называются такие силы, которые действуют на точки или тела механической системы со стороны точек или тел, которые не принадлежат данной системе.}
_{Внутренними}_{, называют такие силы, которые действуют на точки или тела механической системы со стороны точек или тел той же системы, т.е. с которыми точки или тела данной системы взаимодействуют между собой.}

_{Внешние и внутренние силы системы, в свою очередь могут быть активными и реактивными.}

_{Свойства внутренних сил:}

_{Геометрическая сумма (главный вектор) всех внутренних сил системы равняется нулю}
_{Сумма моментов (главный вектор) всех внутренних сил системы относительно какого-нибудь центра}

_{Дифференциальные уравнения поступательного движения твердого тела Если механическая система представляет собой твердое тело, то при поступательном движении скорости и ускорения всех точек в данный момент времени будут иметь одинаковые по модулю и направлению ускорения, поэтому дифференциальное уравнение движения твердого тела в векторной форме имеет вид:}

_{∑= = n k e Fk Ma 1}

_{, где ∑= = n k M mk 1 – масса системы,}

_{∑= n k e Fk 1 – главный вектор внешних сил.}

_{Главный вектор внутренних сил в неизменяемой механической системе равен нулю. 71 При исследовании движения механических систем применяют общие теоремы динамики, устанавливающие связь между мерами движения и мерами действия сил (таблица 1). Общие теоремы динамики представляют собой первые интегралы движения. Общие теоремы динамики справедливы для материальной точки и для механической системы.}

_{16 вопрос.}_{ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС МЕХ. СИСТЕМЫ}

http://student-madi.ru/dlrs/termech-sorokin/dinamika/d.2.2.11.gif

_{Доказательство}

_{Повторим все вышеприведенные предложения; запишем n векторных равенств}

_{(основное уравнение динамики для каждой м.т.) и сложим их.}

http://student-madi.ru/dlrs/termech-sorokin/dinamika/d.2.2.8.gif

_{И используются эти уравнения абсолютно точно так же - то есть для решения первой и второй задач динамики. Подробнее о задачах будет сказано дальше. Здесь же отметим, что записанные уравнения называются также диф. уравнениями поступательного движения твердого тела.}

_{Поступательно движущееся тело в механике рассматривается как материальная точка.}

_{Дифференциальные. уравнения поступательно движущегося тела и м.т., естественно, одинаковы.}

_{При сложном движении твердых тел ( в кинематике сложное движение тела рассматривается как результат сложения поступательного движения и вращательного или сферического) вышеприведенные уравнения описывают поступательную часть движения тела.}

_{Следствия из теоремы о движении центра масс}_{называют}

_{законами сохранения движения или положения центра масс М.С.}

_{Аналогичные следствия с аналогичными формулировками законов сохранения мы получим и из следующих теорем. Поэтому первые законы сохранения мы и сформулируем, и кратко запишем. Формулировки остальных законов сохранения по их кратким записям каждый может и должен для себя получить самостоятельно.}

_{Итак, формулировки законов сохранения движения центра масс имеют следующий вид:}

_{Если главный вектор внешних сил системы равен нулю, то центр масс М.С. либо движется с постоянной по величине и направлению скоростью, либо находится в состоянии покоя.}

_{Если сумма проекций внешних сил на какую либо ось равна нулю, то проекция вектора скорости движения центра масс М.С. на эту ось либо постоянна, либо равна нулю.}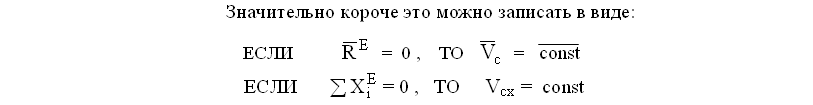

http://student-madi.ru/dlrs/termech-sorokin/dinamika/d.2.2.9.gif

_{Следующие законы сохранения будут записаны только кратко !}

_{Законы сохранения движения центра масс (Ц.М.) позволяют утверждать следующее. Никакие внутренние силы не могут изменить скорость движения Ц.М. М.С..}

_{Причиной движения могут быть только внешние силы. На абсолютно гладкой горизонтальной плоскости никакое движение (исключая реактивное или по инерции ) невозможно.}

_{Представьте себе новичка на льду или автомобиль, трогающийся с места в сильный гололед. Внешней силой, заставляющей двигаться по горизонтальной плоскости автомобиль или любой другой объект, является сила сцепления колес автомобиля или рассматриваемого объекта с поверхностью.}

_{Рассмотрите самостоятельно, как направлена сила трения, когда двигатель заставляет вращаться колесо, соприкасающееся с плоскостью, при движении автомобиля и как изменяется направление силы трения, если заторможенное колесо перестает вращаться.}

_{И еще некоторые примеры действия законов сохранения.}

http://student-madi.ru/dlrs/termech-sorokin/dinamika/d.2.2.4.gif

_{……………………………………………………………………………………………………………………………………………………………………………………………17 вопрос .}

_{Общие теоремы динамики системы точек.}

_{Основные (общие) теоремы динамики систем свободных материальных точек являются уравнениями движения систем свободных материальных точек, т. е. математически дифференциальными уравнениями изменений основных мер движения.}

_1._{Для точки}_{уравнение движения относительно инерциальной системы отсчёта:}

_{Перенесём все векторы, не изменяя их направления, в центр масс и сложим геометрически:}

_.

_{Производная по времени от количества движения системы свободных материальных точек равна геометрической сумме внешних сил.}_{Это теорема об изменении количества движения системы.}

_{Так как}_то

_.

_{Это уравнение движения центра масс системы материальных точек с массой, равной массе всей системы, к которой приложена сумма всех внешних сил (главный вектор внешних сил )}_{или теорема о движении центра масс.}

_2._{Умножим уравнение движения точки}_{слева векторно на}_{и геометрически сложим, перенося векторы в центр масс:}

_.

_{Теорема об изменении кинетического момента системы:}

_{Производная по времени от кинетического момента системы свободных материальных точек равна сумме моментов всех внешних сил (главному моменту всех внешних сил).}

_{Существенно: моменты количества движения и моменты сил вычисляются относительно общего неподвижного начала.}

_3._{Умножая скалярно уравнение движения точки}_на_{и суммируя:}

_или

http://www.toehelp.ru/theory/ter_meh/image022-7.gif

_.

_{Теорема об изменении кинетической энергии системы:}

_{Дифференциал кинетической энергии системы свободных материальных точек равен сумме элементарных работ всех внешних и внутренних сил.}

_{Интегралы уравнений движения системы:}

_{1) Если равен нулю главный вектор внешних сил, то}_{= const, то есть центр масс системы свободных материальных точек движется равномерно и прямолинейно.}

_{2) Если главный момент внешних сил равен нулю, то сохраняется кинетический момент системы свободных материальных точек:}

_.

_{3) Если внешние и внутренние силы консервативны, то}

http://www.toehelp.ru/theory/ter_meh/image028-9.gif

_Здесь:

_{- потенциал внешнего силового поля;}

_{- потенциал взаимодействия точек;}

_{- потенциальная энергия системы точек во внешнем поле;}

_{- потенциальная энергия взаимодействующих точек.}

_{……………………………………………………………………………………………………………………………………..}

_{18 вопрос. Меры механического движения и меры механической силы}

_{В динамике рассматриваются два случая преобразования механического движения материальной точки или системы точек:}

_{1) механическое движение переносится с одной механической системы на другую в качестве механического движения;}

_{2) механическое движение превращается в другую форму движения материи (в форму потенциальной энергии, теплоты, электричества и т. д.).}

_{Каждый из этих случаев преобразования механического движения имеет свои измерители как механического движения, так и действия силы.}_{Когда рассматривается преобразование механического движения без перехода его в другую форму движения}_,_{мерой механического движения является вектор количества движения}_{материальной точки}_{или механической системы}

_.

_{Мерой действия силы в этом случае является вектор импульса силы}_{(см. § 46).}_{Когда механическое движение превращается в другую форму движения материи, в качестве меры механического движения выступает}_{кинетическая энергия}_{материальной точки или механической системы.}

_{Из элементарного курса физики известно, что}_{кинетическая энергия материальной точки}_{массой т, движущейся со скоростью v, равна половине произведения массы этой точки на квадрат скорости ее движения:}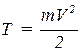

_{Мерой действия силы при превращении механического движения в другую форму движения является}_{работа силы}_{, которая также рассматривается в элементарном курсе физики.}

_{В данной главе рассмотрены различные случаи вычисления работы сил и установлена теорема об изменении кинетической энергии как материальной точки, так и механической системы.}

_Итак,_{существуют две различные меры механического движения}_:

_{количество движения}_и_{кинетическая энергия}

_и_{две различные меры действия силы}_{: импульс силы}_{и работа силы}_.

_{Следует отметить, что измерителями механического движения и действия силы}_{в первом случае}_{являются}_{векторные величины}_и_{, а}_{во втором случае}_-_{скалярные величины}_и_{. Вопрос о выборе меры механического движения был пред метом многолетней полемики между сторонниками Декарта и сторонниками Лейбница.}

_{Декарт считал, что мерой механического движения является количество движения mv, а Лейбниц утверждал, что динамические свойства тел характеризуются величиной mv2. Этот спор был разрешен Ф. Энгельсом, который в своей работе «Диалектика природы»* показал существование двух мер механического движения.}

_{Так как изменение величины mv2/2 связано с работой приложенных к телу сил, то}_работа_{является количественной мерой превращения механического движения в какую-либо другую форму движения.}

_{«При всех явлениях форма движения, начинающая процесс и превращающаяся благодаря ему в другую форму движения, совершает работу и притом такое ее количество, которое соответствует ее собственному количеству... .}_{Механическое движение нигде и никогда не может произвести работу}_,_{если оно не будет по видимости уничтожено}_{как таковое,}_{если оно не превратится в какую-нибудь другую форму движения}_{»**. Так, например, работа сил трения, тормозящих движение тела, работа сил тяжести поднимаемого груза, работа сил упругости пружины, останавливающей движущееся тело, являются мерами уничтожаемого механического движения, которое превращается в теплоту, потенциальную энергию, энергию упругого тела.}

_{…………………………………………………………………………………………………………………………………………………………………………………….}_{19 вопрос.}_{Количество движения системы (импульс системы).}

_{Количество движения (импульс тела)}_{– векторная физическая величина, равная произведению массы тела на его скорость:}

_{Импульс (количество движения) – одна из самых фундаментальных характеристик движения тела или системы тел.}

_{Запишем}_II_{закон Ньютона в другой форме, учитывая, что ускорение}_Тогда

_{следовательно}

_{Произведение силы на время ее действия равно приращению импульса тела (рис. 1):}

_Где_{- импульс силы, который показывает, что результат действия силы зависит не только от ее значения, но и от продолжительности ее действия.}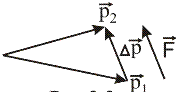

http://www.teoretmeh.ru/dinamika5.files/image016.gif

_Рис.1

_{Количеством движения системы (импульсом) будем называть векторную величину}_{, равную геометрической сумме (главному вектору) количеств движения (импульсов) всех точек системы}_(рис.2):

_{Из чертежа видно, что независимо от величин скоростей точек системы (если только эти скорости не параллельны) вектор}_{может принимать любые значения и даже оказаться равным нулю, когда многоугольник, построенный из векторов}_{, замкнется. Следовательно, по величине}_{нельзя полностью судить о характере движения системы.}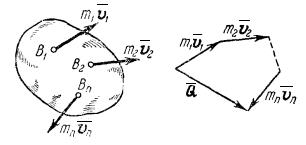

http://www.teoretmeh.ru/dinamika5.files/image025.jpg

_Рис.2

_{Найдем формулу, с помощью которой значительно легче вычислять величину}_{, а также уяснить ее смысл.}

_{Из равенства}

_{следует, что}

_{Беря от обеих частей производную по времени, получим}

_{Отсюда находим, что}

_т.е._{количество движения (импульс) системы равно произведению массы всей системы на скорость ее центра масс}_._{Этим результатом особенно удобно пользоваться при вычислении количеств движения твердых тел.}

_{Из формулы видно, что если тело (или система) движется так, что центр масс остается неподвижным, то количество движения тела равно нулю. Например, количество движения тела, вращающегося вокруг неподвижной оси, проходящей через его центр масс, будет равно нулю.}

_{Если же движение тела является сложным, то величина}_{не будет характеризовать вращательную часть движения вокруг центра масс. Например, для катящегося колеса}

_{независимо от того, как вращается колесо вокруг его центра масс}_С_.

_{Таким образом,}_{количество движения характеризует только поступательное движение системы.}_{При сложном же движении величина}_{характеризует только поступательную часть движения системы вместе с центром масс.}

_{…………………………………………………………………………………………………………………………….}

_{20 вопрос.}_{Теорема об изменении количества движения (импульса).}

_{Рассмотрим систему, состоящую из}_п_{материальных точек. Составим для этой системы дифференциальные уравнения движения}_{и сложим их почленно. Тогда получим:}

_{Последняя сумма по свойству внутренних сил равна нулю. Кроме того,}

_{Окончательно находим:}

_{Уравнение выражает теорему об изменении количества}_{движения}_{(импульса) системы}_в_{дифференциальной форме:}_{производная по времени от количества движения (импульса) системы равна геометрической сумме всех действующих на систему внешних сил}_._{В проекциях на координатные оси будем иметь:}

_{Найдем другое выражение теоремы. Пусть в момент}_t_{=0 количество движения системы равно}_,_{а в момент}_{становится равным}_{. Тогда, умножая обе части равенства}

_на_dt_{и интегрируя, получим:}

_или

_{так как интегралы, стоящие справа, дают импульсы внешних сил.}

_{Уравнение выражает теорему об изменении количества движения системы в интегральной форме:}_{изменение количества движения системы за некоторый промежуток времени равно сумме импульсов действующих на систему внешних сил за тот же промежуток времени.}

_{В проекциях на координатные оси будем иметь:}

_{Укажем на связь между доказанной теоремой и теоремой о движении центра масс. Так как}

_{то, подставляя это значение в равенство и учитывая, что}

_{, мы получим}

_.

_{Следовательно, теорема о движении центра масс и теорема об изменении количества движения системы представляют собой, по существу, две разные формы одной и той же теоремы. В тех случаях, когда изучается движение твердого тела (или системы тел), можно в равной мере пользоваться любой из этих форм.}

_{Практическая ценность теоремы состоит в том, что она позволяет исключить из рассмотрения наперед неизвестные внутренние силы (например, силы давления друг на друга частиц жидкости).}

_{…………………………………………………………………………………………………………………………..}

_{21 вопрос}_{Закон сохранения количества движения (закон сохранения импульса).}

_{Из теоремы об изменении количества движения системы можно получить следующие важные следствия:}

_{1) Пусть сумма всех внешних сил, действующих на замкнутую систему, равна нулю:}

_{Тогда из уравнения}

_{следует, что}_Q₌₌_const_{. Таким образом,}_{если сумма всех внешних сил, действующих на замкнутую систему, равна нулю, то вектор количества движения (импульса) системы будет постоянен по модулю и направлению.}

_{2) Пусть внешние силы, действующие на систему, таковы, что сумма их проекций на какую-нибудь ось (например}_О_x_{) равна нулю:}

_{Тогда из уравнения}

_{следует, что при этом}_Qx₌_const_{. Таким образом,}_{если сумма проекций всех действующих внешних сил на какую-нибудь ось равна нулю, то проекция количества движения (импульса) системы на эту ось есть величина постоянная.}

_{Эти результаты и выражают}_{закон сохранения количества движения системы:}_{при любом характере взаимодействия тел, образующих замкнутую систему, вектор полного импульса этой системы все время остается постоянным.}

_{Из них следует, что внутренние силы изменить суммарное количество движения системы не могут.}

_{Закон сохранения полного импульса изолированной системы – это универсальный закон природы. В более общем случае, когда система незамкнута,}_из

_{следует, что}_полный_{импульс незамкнутой системы не остается постоянным. Его изменение за единицу времени равно геометрической сумме всех внешних сил.}

_{Рассмотрим некоторые примеры:}

_{а) Явление отдачи или отката. Если рассматривать винтовку и пулю как одну систему, то давление пороховых газов при выстреле будет силой внутренней. Эта сила не может изменить суммарное количество движения системы. Но так как пороховые газы, действуя на пулю, сообщают ей некоторое количество движения, направленное вперед, то они одновременно должны сообщить винтовке такое же количество движения в обратном направлении. Это вызовет движение винтовки назад, т.е. так называемую отдачу. Аналогичное явление получается при стрельбе из орудия (откат).}

_{б) Работа}_{гребного}_винта_{(пропеллера). Винт сообщает некоторой массе воздуха (или воды) движение вдоль оси винта, отбрасывая эту массу назад. Если рассматривать отбрасываемую массу и самолет (или судно) как одну систему, то силы взаимодействия винта и среды как внутренние не могут изменить суммарное количество движения этой системы. Поэтому при отбрасывании массы воздуха (воды) назад самолет (или судно) получает соответствующую скорость движения вперед, такую, что общее количество движения рассматриваемой системы останется равным нулю, так как оно было нулем до начала движения.}

_{Аналогичный эффект достигается действием весел или гребных колес.}

_{в) Реактивное движение. В реактивном снаряде (ракете) газообразные продукты горения топлива с большой скоростью выбрасываются из отверстия в хвостовой части ракеты (из сопла реактивного двигателя). Действующие при этом силы давления будут силами внутренними, и они не могут изменить суммарное количество движения системы ракета - продукты горения топлива. Но так как вырывающиеся газы имеют известное количество движения, направленное назад, то ракета получает при этом соответствующую скорость движения вперед.}

_{Пример 1.}_{На рельсах стоит платформа массой}_m_{1=10 т. На платформе закреплено орудие массой}_m_{2=5 т, из которого производится выстрел вдоль рельсов. Масса снаряда}_m_{3=100 кг; его начальная скорость относительно орудия}_v_{0=500 м/с. Найти скорость}_{платформы в первый момент после выстрела, если: 1) платформа стояла неподвижно (}_v_{= 0);}₂₎_{платформа двигалась со скоростью}_v_{= 18 км/ч, а выстрел был произведен в направлении ее движения; 3) платформа двигалась со скоростью}_v_{= 18 км/ч, а выстрел был произведен в направлении, противоположном направлению ее движения.}

_{Решение.}_{Для решения задачи воспользуемся законом сохранения импульса, утверждающим, что импульс замкнутой системы остается постоянным.}

_{Запишем импульс системы, состоящей из пушки, орудия и снаряда, до выстрела}₍₎_{и после него (}_{), в результате которого этот импульс меняется. Напомним, что суммарный импульс системы представляет собой векторную сумму импульсов тел, входящих в систему.}

₁₎_{Импульс системы до выстрела}

_{т.к. вначале платформа с орудием покоилась (}_v_=0).

_{После выстрела импульс системы}

_{По закону сохранения импульса}_{, следовательно,}

_{Спроецируем это уравнение на выбранную ось}_х_(рис.3):

_{…………………………………………………………………………………………………………………………}

_{22 вопрос.}

http://extm10.narod2.ru/sem3/vop/09_5.jpg

_{Твердое тело, вращающееся вокруг неподвижной оси z (рис. 25), можно рассматривать как систему точек. Момент количества движения этой системы относительно оси z называют}_{кинетическим моментом}_{твердого тела относительно оси вращения:}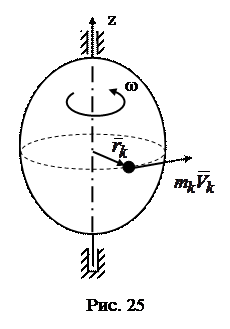

http://ok-t.ru/studopediaru/baza8/492027761286.files/image481.gif

_{Учитывая, что при вращательном движении:}

_{, а}

_{, получим}

_{. По формуле (34) получим}

₍₄₅₎

_–_{кинетический момент твердого тела вращающегося вокруг неподвижной оси равен произведению момента инерции тела относительно оси вращения на его угловую скорость.}

_{……………………………………………………………………………………………………………………………………}

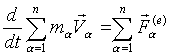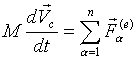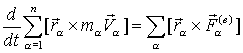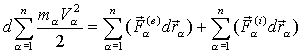
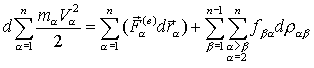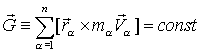1 2 3 4 5 6 7 8 9 10 11

1 вопрос. Динамика точки. Основные понятия и определения

14 вопрос. Классификация сил, действующих на механическую систему: силы внешние и внутренние, активные и реакции связей.

2)Физический маятник. Опытное определение моментов инерции тел.

_{14 вопрос.}_{Классификация сил, действующих на механическую систему: силы внешние и внутренние, активные и реакции связей.}

_{2)Физический маятник. Опытное определение моментов инерции тел.}