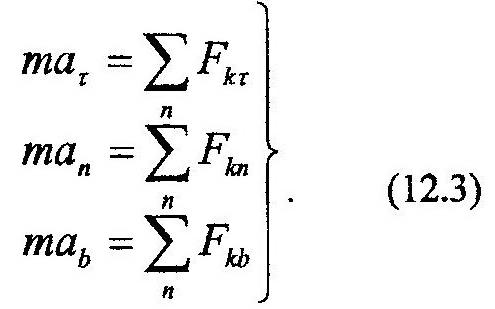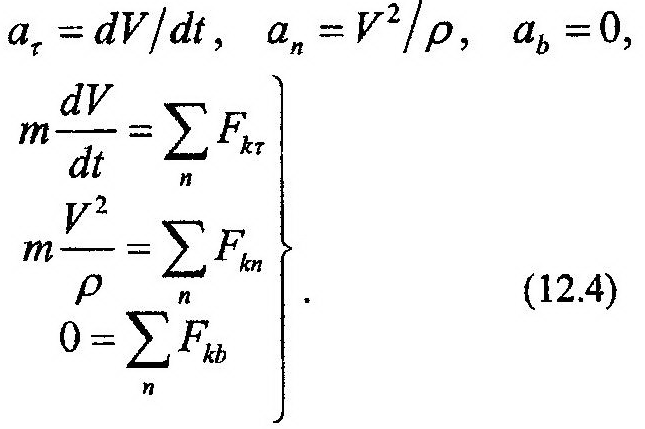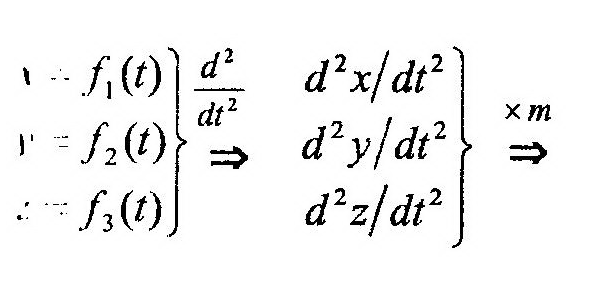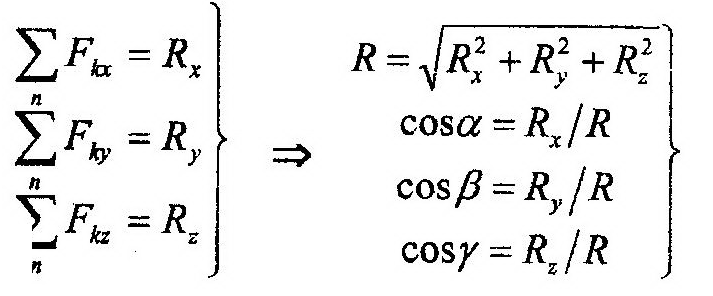1 вопрос. Динамика точки. Основные понятия и определения

Название	1 вопрос. Динамика точки. Основные понятия и определения
Дата	19.06.2018
Размер	1.54 Mb.
Формат файла
Имя файла	teor_mekh_ekz.docx
Тип	Документы #47317
страница	2 из 11

1 2 3 4 5 6 7 8 9 10 11

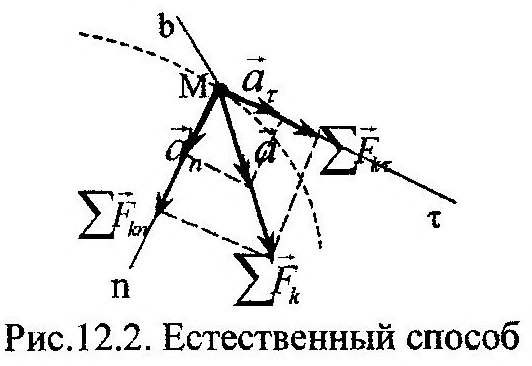
_{5 вопрос.}_{Уравнения движения в векторной форме}

_{Уравнения движения ЛА}

_{Движение ЛА рассматривается относительно выбранной системы отсчета на поверхности Земли, или в центре масс Земли. Для инерциальной системы отсчета, движущейся прямолинейно равномерно относительно «абсолютно неподвижного пространства» движение твердого тела описывается векторными уравнениями [1], [2]}

_;

_{, (5.1)}

_где_и_{главный вектор и момент количества движения твердого тела относительно его центра масс (тяжести),}_и_{– главные вектор и момент, относительно центра масс всех внешних сил, действующих на твердое тело. ЛА не являются твердым телом и должен рассматриваться как система переменного состава. Для этой цели можно считать …
ЛА мгновенно затвердевшим телом и добавить для фиктивного ”затвердевшего” тела реактивные силы, внутренние силы Кориолиса и вариационные силы, которые обозначим}_.

_{Внутренние кориолисовы силы инерции возникают из-за относительного движения масс внутри твердой оболочки тела при ее вращении. Вариационные силы обусловлены нестационарностью движения масс внутри твердой оболочки.}

_{Часто группу сил: реактивную силу, статические силы от разности атмосферного давления и давления газов во входном сечении воздухозаборника и во входном сечении сопла и вариационные силы объединяют вместе и называют силой тяги двигателя и обозначают вектором}_{. Иногда различают понятия двигатель и движитель.}

_{Движитель}_{– это агрегат, создающий силу тяги, а}_{двигатель}_{– источник энергии.}

_{Внутренние кориолисовы и вариационные силы}_{обычно малы и ими пренебрегают по сравнению с силами внешними и реактивными.}

_{По принципу «затвердевания» (}_m=const,_при_t=const_{) для главного вектора}_{количества движения твердого тела можно записать в общем виде:}

_{…, (5.2)}

_{(Сравним: второй закон Ньютона-}_),

_где_m_{-масса ЛА,}_{–вектор абсолютной скорости центра масс ЛА,}_{– вектор ускорения центра масс.}

_{Главный момент}_{количества движения относительно центра масс твердого тела определяется формулой:}

_{. (5.3)}

_Здесь_{– момент внутренних кориолисовых сил.}

_{Если система отсчета движения принимается неинерциальной, то в правую часть (5.2) добавляются соответственно кориолисовы и переносные силы инерции, а в (5.3) – моменты этих сил.}

_{6 вопрос.}_{Координатная форма записи уравнения движения.}

как записывается в координатной форме уравнение равномерного прямолинейного движения точки, если она движется: по оси oy; по оси oz?

как записывается в координатной форме уравнение равномерного прямолинейного движения точки, если она движется: по оси oy; по оси oz?

_{………………………………………………………………………………………………………………………}

_{7 вопрос.}_{Естественная форма записи уравнения движения.}

_{В тех случаях, когда траектория движения точки определена заранее, успешно используют в решении задач естественный способ задания движения точки. Уравнения движения точки, соответствующие данному способу, получим, проектируя обе части выражения основного закона динамики (11.1) на оси}_{τ, n, b}_{(рис. 12.2):}


_{получим:}	_{Учитывая, что:}

_{В (12.4) только в первые два уравнения входит кинематический параметр, характеризующий движение точки, это –}_V_{. Последнее выражение в (12.4) по своему виду соответствует уравнению равновесия – уравнению статики. Из всех уравнений (12.4) только первое является дифференциальным. Таким образом, уравнения движения точки, соответствующие естественному способу, являются более простыми по своему виду. В этом их преимущество над уравнениями вида (12.2).}

_{Задачи динамики}

_{Все задачи динамики можно условно поделить на}_{две группы:}_{первая (прямая)}_и_{вторая (обратная)}_{задачи. Условность деления заключается в том, что не все задачи один к одному соответствуют формулировкам, указанным ниже. Возможно и их сочетание в пределах одной задачи.}

_{В прямых задачах:}_{по известным уравнениям движения точки определяют силы,вызыв}_{ающие его.}

_{Таким образом, исходными для решения первой задачи динамики точки являются ее уравнения движения, записанные в одном из видов: векторном, координатном или естественном (см. тему: «способы задания движения точки»). Например, в координатной форме записи эти уравнения связывают координаты точки (}_{x, y, z}_{) с временем (}_t_).

_{Алгоритм решения первой (прямой) задачи}_{представлен ниже:}

http://helpiks.org/helpiksorg/baza7/673127405333.files/image149.png

http://helpiks.org/helpiksorg/baza7/673127405333.files/image150.png

_{По известным уравнениям движения находят вторые производные от координат по времени и, умножая их на массу точки,}_m_{, определяют правые части выражений (12.2). Модуль равнодействующей,}_R_{, системы сходящихся сил, приложенных к точке, равен длине диагонали параллелепипеда, построенного на проекциях}_Rx_,_Ry_,_Rz_{как на сторонах. С помощью направляющих косинусов можно определить направление вектора равно-действующей в пространстве.}

_{………………………………………………………………………………………………………………………………………………………………………………………}

_{8 вопрос.}_{Две основные задачи динамики.}

_{В динамике решаются две основных задачи:}

₁₎_{по заданному движению точки или системы определить силы, производящие это движение.}

₂₎_{по заданным силам, действующим на точку или систему, определить движение этих объектов.}

_{Когда мы говорим, что задано движение точки, то предполагаем, что ее движение задано одним из кинематических способов (естественным, координатным или векторным). Когда мы определяем движение точки по заданным силам, то это значит, что мы стремимся выразить движение точки одним из кинематических способов, т.е. ищем координаты как функции времени, или закон движения точки по траектории, или закон изменения радиус-вектора точки.}

_{Пусть на точку с массой}_m_{действует система сил}_{. Основное уравнение динамики точки:}

_(*)_{, где}_{- равнодействующая всех активных сил и реакций связей.}

_{Спроектируем обе части этого векторного равенства на оси декартовых координат:}

_;_;_;_;_{, тогда}

_;_;₍₁₎

_{Это дифференциальные уравнения движения материальной точки в декартовых координатах.}

_{Иногда при решении задач о движении точки пользуются диф. уравнениями в проекциях на естественные оси координат. Для получения этих уравнений спроектируем обе части уравнения (*) на касательную, главную нормаль и бинормаль:}

_;_;

_{Проекция ускорения на бинормаль равна 0, проекции на касательную и главную нормаль равны:}

_и_{, поэтому}

_;_;₍₂₎

_{Это естественные уравнения движения материальной точки. С помощью этих уравнений многие задачи динамики точки, особенно такие, в которых известна траектория точки, решаются проще, чем при помощи уравнений (1).}

_{Обе основные задачи динамики решаются при помощи уравнений (1) и (2).}

_{Решение первой основной задачи динамики}_.

_{Пусть движение точки массой}_m_{задано координатным способом, т.е. заданы}

_x₌_f₁₍_t_);_y₌_f₂₍_t_);_z₌_f₃₍_t₎

_{Дифференцируя дважды по}_t_{и подставляя значения}_{в уравнения (1):}_,_,_.

_{Модуль и направляющие косинусы равнодействующей найдем по формулам:}

_;_;_;

_{Если движение задано естественным способом:}_S₌_f₍_t₎

_,_,_,_,

_{………………………………………………………………………………………………………………………………}

_{9 вопрос.}_{Решение второй задачи динамики}_:

_{В общем случае равнодействующая}_{будет зависеть от времени, координат точки и ее скорости.}

_{после интегрирования}

_x₌_f₁₍_t_,_c_1,_c_2,_c_3,_c_4,_c_5,_c₆₎_{Чтобы выбрать из семейства одну определенную}

_y₌_f₂₍_t_,_c_1,_c_2,_c_3,_c_4,_c_5,_c₆₎_{траекторию, следует придать параметрам}_c_1,…,_c₆

_z₌_f₃₍_t_,_c_1,_c_2,_c_3,_c_4,_c_5,_c₆₎_{конкретные значения.}_Их_{находят с помощью начальных условий.}

_{………………………………………………………………………………………………………………………………}

_{10 вопрос.}_{Интегрирование дифференциальных уравнений движения материальной точки}

_{Из теории дифференциальных уравнений известно, что при интегрировании уравнения второго порядка появляются две произвольных постоянных интегрирования.}

_{Следовательно, при интегрировании системы (4) появятся шесть постоянных интегрирования. Таким образом, решение системы (4) будет иметь вид}

_{x = x(t,C1,C2,C3,C4,C5,C6)}

_{y = y(t,C1,C2,C3,C4,C5,C6)}

_{z = z(t,C1,C2,C3,C4,C5,C6)}_{, (6)}

_где_{C1,C2,C3,C4,C5,C6}_{− постоянные интегрирования.}

_{В зависимости от постоянных интегрирования получается целый класс решений, удовлетворяющих системе уравнений (4).}

_{Чтобы получить конкретное решение, необходимо определить постоянные интегрирования.}

_{Для этого необходимо знать значение координат и скорости точки в какой-либо момент времени (обычно в начальный), поэтому эти значения называют начальными условиями.}

_{Таким образом, решение (6) можно переписать в виде}

_{x = x(t,x0,y0,z0,vx0,vy0,vz0)}

_{y = y(t,x0,y0,z0,vx0,vy0,vz0)}

_{z = z(t,x0,y0,z0,vx0,vy0,vz0}₎_{, (6’)}

_{11 вопрос. Определение постоянных интегрирования.}

_{Определение постоянных интегрирования производится на заключительном этапе расчета переходного процесса, когда остальные составляющие решения уже найдены. Постоянные интегрирования определяются путем подстановки в решение для искомой функции соответствующих начальных условий.}

_{Пусть решение для искомой функции i(t) содержит только одну постоянную интегрирования:}

_{Постоянная интегрирования находится путем подстановки в решение начального условия для самой функции, т.е. i(0):}

_{Пусть решение для искомой функции i(t) содержит две постоянных интегрирования и имеет вид:}

_{Постоянные интегрирования в этом случае находятся путем подстановки в решение начальных условий для самой функции i(0) и для ее первой производной di/dt(0):}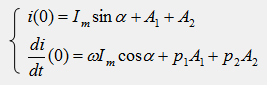

определение постоянных интегрирования

_{В результате совместного решения этой системы уравнений определяют искомые постоянные интегрирования А1 и А2 .}

_{/…………………………………………………………………………………………………………………………………….}

₁₂_{вопрос . Динамика относительного движения материальной точки}

_{Динамика относительного движения материальной точки}

_{Второй закон динамики и полученные на его основе уравнения и теоремы верны только для так называемого абсолютного движения точки, то есть движения по отношению к инерциальной (неподвижной) системе отсчета.}

_{Изучим движение материальной точки относительно неинерциальной системы отсчета, то есть подвижной системы отсчета. Рассмотрим материальную точку}_{, движущуюся под действием приложенных к ней сил}_{, являющихся результатом взаимодействия точки с другими телами. Будем изучать движение этой точки по отношению к осям}_{, которые в свою очередь каким-то известным нам образом движутся относительно инерциальной системы отсчета (неподвижных осей)}_(рис.1).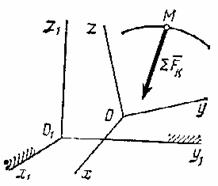

http://www.teoretmeh.ru/ukazandinamika.files/image010.jpg

_Рис.1

_{Движение точки}_{относительно системы}_{называется абсолютным, а движение этой точки относительно системы}_{- относительным. Движение подвижной системы}_{относительно неподвижной системы}_{называется переносным движением.}

_{Считая, что переносное движение системы}_{и система сил}_{известны, основное уравнение динамики для абсолютного движения точки}_{запишется в виде}

_{,                                                (1)}

_где_{- абсолютное ускорение точки}_{, а}_{- геометрическая сумма приложенных к точке сил.}

_{Из кинематики известно, что}

_где_{- соответственно относительное, переносное и кориолисово ускорения точки}_.

_{Подставляя это значение}_{в равенство (1) получим}

_{.                                         (2)}

_{Введем два вектора}_,

_{численно равные}_и_{и направленные противоположно ускорениям}_и_._{Эти векторы назовем переносной и кориолисовой силами инерции}_.

_{Подставим эти векторы в уравнение (2)}

_{.                                          (3)}

_{Уравнение (3) представляет собой основное уравнение динамики относительного движения материальной точки. Сопоставив (1) и (3) заключаем:}_{в случае непоступательного переносного движения относительное движение материальной точки можно рассматривать как абсолютное, если к действующим на точку силам присоединить переносную и кориолисову силы инерции.}

_{Это сопоставление показывает также, что в инерциальной системе отсчета ускорение точки является лишь результатом действия на нее сил, в то время как в неинерциальной системе ускорение является как результатом действия на нее сил, так и результатом движения самой системы отсчета.}

_{Спроектировав (3) на оси подвижной системы отсчета}_{, получим дифференциальные уравнения относительного движения материальной точки}

_,

_{,                                                                   (4)}

_.

_{Рассмотрим частные случаи относительного движения материальной точки, соответствующее различным видам переносного движения.}

_{1. Переносное движение – неравномерное вращение тела вокруг неподвижной оси. В этом случае переносное ускорение}_{равно геометрической сумме вращательного и центростремительного ускорений}

_.

_{Тогда уравнение (3) принимает вид}

_{,                                       (5)}

_где_,_.

_{2. Переносное движение – равномерное вращение тела вокруг неподвижной оси. В этом случае}_{, а следовательно,}_{. Тогда уравнение (3) запишется в виде}

_{.                                                (6)}

_{3. Переносное движение – поступательное неравномерное криволинейное движение. В этом случае}_и_{, а потому}

_{.                                                          (7)}

_{4. Переносное движение – поступательное прямолинейное и равномерное движение. В  этом случае}_и_{, а потому}

_{.                                                                                      (8)}

_{Сопоставив (8) и (1) замечаем, что их правые части совпадают. Это говорит о том, что подвижная система отсчета}_{является в этом случае тоже инерциальной системой.}

_{Рассмотрим пример решения задачи.}

_{Дифференциальные уравнения движения точки}

_{Пусть на материальную точку действует некоторая система сил и требуется определить движение точки под действием этих сил.}

_{Уравнение второго закона динамики для материальной точки массой}_m_{запишется в виде}

_{m⋅ a = ΣFi}₍₁₎

_где_a_{- ускорение точки;}

_Fi_{- силы, действующие на точку, включая реакции связей.}

_{Спроецировав уравнение (1) на декартовы оси координат, получим систему из трех уравнений}

_{m⋅ ax = ΣFxi}

_{m⋅ ay = ΣFyi}₍₂₎

_{m⋅ az = ΣFzi}

_где_ax_,_ay_,_az_{- проекции ускорения точки на декартовы оси координат;}

_Fxi_,_Fyi_,_Fzi_{- проекция i-той силы на соответствующую ось.}

_{Учитывая, что}

_{получаем систему дифференциальных уравнений первого порядка относительно проекций скорости точки}

_{или второго порядка относительно координат точки}

_{Спроецировав уравнение (1) на естественные оси координат, получим следующую систему уравнений}

_где_aτ_и_an_{- касательное и нормальное ускорение точки;}

_Fτi_,_Fni_,_Fbi_{- проекция i-той силы на касательную, нормаль и бинормаль соответственно.}

_{Учитывая, что}

_{aτ = dV/dt, an = V2/ρ, ab = 0}

_{получим:}

_{mdV/dt = ΣFτi ,}

_{mV2/ρ = ΣFni ,}₍₅₎

_{0 = ΣFbi .}

_{В зависимости от того, что известно о движении точки, дифференциальные уравнения записывают или в декартовых или в естественных координатах.}

_{13вопрос.}_{Динамическая теорема Кориолиса.}

_{Пусть точка}_М_{под действием приложенных к ней сил}

_{движется по отношению к осям}_XOYZ_{. Эти оси движутся по отношению к инерциальной системе отсчета (например, неподвижным осям)}

_.

_{По теореме Кориолиса абсолютное ускорение точки}_М_равно:

_.

_{Основной закон динами для точки}_М_:

_{Обозначим:}

_-_{переносная сила инерции;}

_-_{кориолисова сила инерции.}

_.

_{Это основной закон динамики для относительного движения точки (общий случай) -}_{динамическая теорема Кориолиса: Материальная точка движется относительно неинерциальной системы отсчета также как относительно инерциальной, только к действующим силам надо прибавить переносную и кориолисову силу инерции.}

_{Частные случаи:}

_{ü Подвижные оси}_XOYZ_{движутся поступательно.}_{Угловая скорость подвижных осей}

_.

_{ü Подвижные оси}_XOYZ_{движутся поступательно равномерно и прямолинейно.}

_.

_{В этом случае закон относительного движения аналогичен абсолютному движению.}

_{Следствие:}_{Система отсчета, движущаяся поступательно равномерно и прямолинейно, является инерциальной.}_{В ней выполняются принципы относительности Галилея и Эйнштейна.}

_{ü Точка}_М_{покоится по отношению к подвижным осям:}

_.

_{Это уравнение относительного равновесия (покоя) точки (тела). То есть уравнения относительного равновесия составляют также как уравнения равновесия в неподвижных осях, но при этом к действующим на точку (тело) силам прибавляют переносную силу инерции}

_{……………………………………………………………………………………………………………………………………}

1 2 3 4 5 6 7 8 9 10 11

1 вопрос. Динамика точки. Основные понятия и определения

5 вопрос. Уравнения движения в векторной форме

В общем случае равнодействующая будет зависеть от времени, координат точки и ее скорости.

10 вопрос. Интегрирование дифференциальных уравнений движения материальной точки

Дифференциальные уравнения движения точки

_{5 вопрос.}_{Уравнения движения в векторной форме}

_{В общем случае равнодействующая}_{будет зависеть от времени, координат точки и ее скорости.}

_{10 вопрос.}_{Интегрирование дифференциальных уравнений движения материальной точки}

_{Дифференциальные уравнения движения точки}