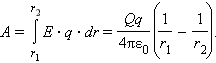ждлормсчсмитьлд. 1 Вопрос. Формулировка Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними

• Название: 1 Вопрос. Формулировка Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними
• Анкор: ждлормсчсмитьлд
• Дата: 09.04.2022
• Размер: 0.97 Mb.
• Имя файла: Fizika_ekzamen.docx
• Тип: Закон; #456698
• страница: 1 из 3

1 Вопрос.

Формулировка: Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними.

где   – электрическая постоянная.

Полевая трактовка закона Кулона:

Если пробный заряд находится в точке пространства, в которой присутствуют поля нескольких точечных зарядов, то выполняется принцип независимости действия сил: Результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.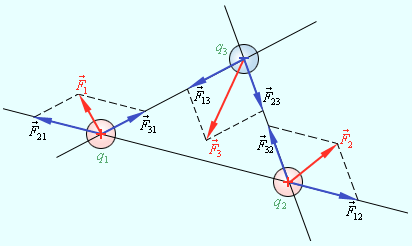



При заданном распределении зарядов на всех телах силы электростатического взаимодействия между любыми двумя телами не зависят от наличия других заряженных тел.

Электрические заряды не действуют друг на друга непосредственно. Каждое заряженное тело создает в окружающем пространстве электрическое поле. Это поле оказывает силовое действие на другие заряженные тела. Главное свойство электрического поля – действие на электрические заряды с некоторой силой. Для количественного определения электрического поля вводится силовая характеристика - напряженность электрического поля.

2 Вопрос.

Принцип суперпозиции:

• 
  сила взаимодействия двух точечных зарядов не изменяется, если присутствуют другие заряды;
  
• 
  сила, действующая на точечный заряд со стороны двух других точечных зарядов, равна сумме сил, действующих на него со стороны каждого из точечных зарядов при отсутствии другого.
  

В случае, когда речь идет о множестве зарядов N (т.е. нескольких источников поля), суммарную силу, которую испытывает на себе пробный заряд q, можно определить по формуле:

,

где   является силой, с которой влияет на заряд q зарядq_i, если прочий N^-1 заряд отсутствует.

Полевая трактовка принципа суперпозиции

Полевая трактовка: напряженность поля двух точечных зарядов есть сумма напряженностей, создаваемым каждым из зарядов при отсутствии другого.

Для общих случаев принцип суперпозиции относительно напряженностей имеет следующую запись: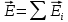

,

где   является напряженностью i-го точечного заряда,  - радиусом вектора, проложенного от i-го заряда в некоторую точку пространства.

4 вопрос.

Теорема Гаусса позволяет сравнительно просто рассчитать электрические поля при симметрично распределённых зарядов.

Введём понятие о плотности распределенных зарядов.

Линейная плотность обозначается τ и характеризует заряд q, приходящийся на единицу длины ℓ. В общем виде может быть рассчитана по формуле

.

При равномерном распределении зарядов линейная плотность равна  .

Поверхностная плотность обозначается σ и характеризует заряд q, приходящийся на единицу площади S. В общем виде определяется по формуле

.

При равномерном распределении зарядов по поверхности поверхностная плотность равна  .

Объёмная плотность обозначается ρ, характеризует заряд q, приходящийся на единицу объёма V. В общем виде определяется по формуле

.

5 вопрос.

При перемещении пробного заряда q в электрическом поле электрические силы совершают работу. Эта работа при малом перемещении  равна (рис. 1):

Рисунок 1. Работа электрических сил при малом перемещении  заряда q.

Электростатическое поле обладает важным свойством: работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.Аналогичным свойством обладает и гравитационное поле, и в этом нет ничего удивительного, так как гравитационные и кулоновские силы описываются одинаковыми соотношениями.

Следствием независимости работы от формы траектории является следующее утверждение: работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Силовые поля, обладающие этим свойством, называют потенциальными или консервативными.

На рис. 2 изображены силовые линии кулоновского поля точечного заряда Q и две различные траектории перемещения пробного заряда q из начальной точки (1) в конечную точку (2). На одной из траекторий выделено малое перемещение  Работа ΔA кулоновских сил на этом перемещении равна 

Таким образом, работа на малом перемещении зависит только от расстояния r между зарядами и его изменения Δr. Если это выражение проинтегрировать на интервале от r = r₁ до r = r₂, то можно получить 

Рисунок 1.4.2. Работа кулоновских сил при перемещении заряда q зависит только от расстояний r1 и r2 начальной и конечной точек траектории

6 вопрос.

Физическая величина (φ), численно равная:

(1)

есть потенциал поля в заданной точке.

Она используется для описания электрических полей на ряду, с напряженностью. Уравнение (1) показывает, что потенциал равен потенциальной энергии (W_p), которой обладал бы единичный положительный заряд. Потенциал точечного заряда в системе СИ равен:

(2).

В системе СГС:
(3),

где - диэлектрическая проницаемость среды (в обеих формулах).
Потенциал поля, которое создается системой зарядов, равен алгебраической сумме потенциалов, которые создают отдельные заряды: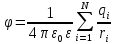

(4).

Допустим, что заряды находятся в области пространства объема V. Заряд непрерывно распределен в этой области с плотностью , тогда потенциал может быть найден как:
(5).

Работа сил поля по перемещению заряда q может быть выражена с использованием разности потенциалов:
(7),

где 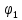- потенциал начальной точки, - потенциал конечной точки. Принято считать, что потенциал равен нулю в бесконечности. Единицей потенциала в системе СИ является вольт (В).


9 вопрос.

Вещество, имеющее свободные частицы с зарядом, двигающиеся по телу за счет действующего электрического поля упорядоченно, называют проводник в электростатическом поле. А заряды частиц называют свободными.

Проводник

В электростатическом поле проводники — металлы, щелочные, кислые и солевые растворы, а также ионизированные газы. Носители свободных зарядов в металлах — это свободные электроны.

При поступлении в однородное электрическое поле, где металлы - проводники без заряда, начнется движение в направлении, которое противоположно вектору напряжения поля. Скапливаясь на одной стороне, электроны создадут отрицательный заряд, а на другой стороне недостаточное их количество станет причиной появления избыточного положительного заряда. Получится, что заряды разделятся. Некомпенсированные разные заряды возникают под воздействием внешнего поля. Таким образом, они индуцированы, а проводник в электростатическом поле остается без заряда.

Проводник в электростатическом поле — это тело из металла, где электроны начинают движение против силовых линий и начнут накапливаться слева. Проводник справа потеряет электроны и получит положительный заряд. При разделении зарядов он обретет свое электрическое поле. Это называется электростатической индукцией.

Внутри проводника напряженность электростатического поля нулевая, что легко доказать, двигаясь от обратного.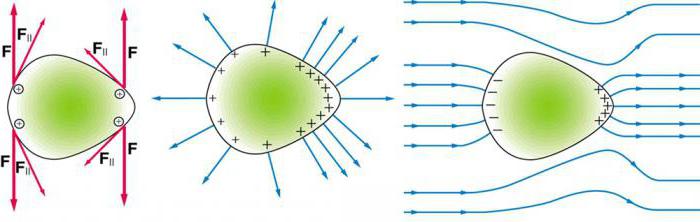



16 вопрос.

Ток в газах

Газы становятся проводниками лишь тогда, когда они каким-то образом ионизированы. Процесс ионизации газов заключается в том, что от атома отрывается один или несколько электронов. В результате этого вместо нейтрального атома возникают положительный ион и электрон. Распад молекул на ионы и электроны называется ионизацией газа.

Таким образом, в ионизованном газе имеются носители зарядов трех сортов: электроны, положительные ионы и отрицательные.

Факторы, вызывающие ионизацию газа, называются ионизаторами. Различают три вида ионизации: термоионизацию, фотоионизацию и ударную ионизацию.

• 
  Термоионизация происходит в результате столкновения атомов или молекул газа при высокой температуре, если кинетическая энергия относительного движения сталкивающихся частиц превышает энергию связи электрона в атоме.
  
• 
  Фотоионизация происходит под действием электромагнитного излучения (ультрафиолетового, рентгеновского или γ-излучения), когда энергия, необходимая для отрыва электрона от атома, передается ему квантом излучения.
  
• 
  Ионизация электронным ударом (или ударная ионизация) — это образование положительно заряженных ионов в результате столкновений атомов или молекул с быстрыми, обладающими большой кинетической энергией, электронами.
  

Газовый разряд

При помещении ионизированного газа в электрическое поле на свободные заряды начинают действовать электрические силы, и они дрейфуют параллельно линиям напряженности: электроны и отрицательные ионы — к аноду, положительные ионы — к катоду (рис. 1). На электродах ионы превращаются в нейтральные атомы, отдавая или принимая электроны, тем самым замыкая цепь. В газе возникает электрический ток.



Рис. 1

Электрический ток в газах — это направленное движение ионов и электронов. Электрический ток в газах называется газовым разрядом.

17 вопрос.

Сила Лоренца.

Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. Фактически эта сила

(16.11) Или  , где 

Перейдем к силе, действующей на проводник с током длиной L. Тогда  =  и  .

Но ток можно представить как  , где   — средняя скорость, n – концентрация частиц, S – площадь поперечного сечения. Тогда

, где  . (16.12)

Так как  ,  . Тогда  , где   — сила Лоренца, т. е. сила, действующая на заряд, движущийся в магнитном поле. В векторном виде

 (16.13)

При   сила Лоренца равна нулю, т. е. она не действует на заряд, который движется вдоль направления  . При  , т. е. сила Лоренца перпендикулярна скорости:  .

Как известно из механики, если сила перпендикулярна скорости, то частицы движутся по окружности радиуса R, т. е.  ,  .

Из уравнения   найдем R:  .

Время одного оборота (период вращения) отдельной формулой равен:

(16.14).

Если частица влетает в магнитное поле под углом   к направлению индукции   со скоростью V, то она движется по винтовой линии, радиус которой R и шаг – 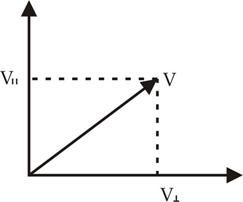h.

Разложим скорость на две составляющие:   и  . Тогда сила Ампера  . По II закону Ньютона  , где   =  , т. е.

 =>  =

Начинаю двигаться по окружности с радиусом R, частица движется при этом равномерно с   вдоль направления  .

Второй параметр винтовой линии – это ее шаг h – смещение вдоль направления   за время оборота  , т. е.  .

Если заряженная частица влетает с некоторой скоростью в электрическое и магнитное поле, то результирующая сила, действующая на частицу равна

(16.14)

В зависимости от ориентации векторов   и   частица может двигаться по разным траекториям, например, по циклоиде.

Взаимодействие элементов тока.

В этом же году Био и Савар сформулировали закон для силы dF, с которой элемент тока I DL действует на магнитный полюс, удаленный на расстояние R от элемента тока:

DF   I dL  (16.1)

Где   – угол, характеризующий взаимную ориентацию элемента тока и магнитного полюса. Функция   вскоре была найдена экспериментально. Функция F(R) Теоретически была выведена Лапласом в виде

F(R) 1/r . (16.2)

Таким образом, усилиями Био, Савара и Лапласа была найдена формула, описывающая силу действия тока на магнитный полюс.

В 1820г. Ампер открыл взаимодействие токов – притяжение или отталкивание параллельных токов. Им была доказана эквивалентность соленоида и постоянного магнита. Можно с полным основанием считать Ампера автором закона магнитного взаимодействия токов. Используемая в настоящее время формула для взаимодействия элементов тока была получена в 1844г. Грассманом.

Если ввести 2 элемента тока   и  , то сила, с которой элемент тока   действует на элемент тока   будет определяться следующей формулой:

, (16.2)

Где  Н/A

Т очно также можно записать:

 (16.3)

Легко видеть: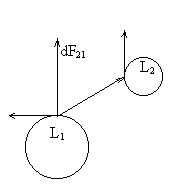



Так как векторы   и   имеют между собой угол не равный 180°, то очевидно  , т. е. III-ий закон Ньютона для элементов тока не выполняется. Но если вычислить силу, с которой ток  , текущий по замкнутому контуру  , действует на ток  , текущий по замкнутому контуру  :

, (16.4)

А затем вычислить  , то  , т. е. для токов Ш-ий закон Ньютона выполняется.

Описание взаимодействия токов с помощью магнитного поля.

В полной аналогии с электростатикой взаимодействие элементов тока представляется двумя стадиями: элемент тока  в месте нахождения элемента   создает магнитное поле, которое действует на элемент   с силой  . Поэтому элемент тока   создает в точке нахождения элемента тока   магнитное поле с индукцией

. (16.5)

На элемент  , находящийся в точке с магнитной индукцией  , действует сила

 (16.6)

Соотношение (16.5), которое описывает порождение магнитного поля током, называется законом Био-Савара. Проинтегрировав (16.5) получим:

 (16.7)

Где   — радиус-вектор, проведенный от элемента тока   к точке, в которой вычисляется индукция  .

Для объемных токов закон Био-Савара имеет вид:

, (16.8)

Где j – плотность тока.

Из опыта следует, что для индукции магнитного поля справедлив принцип суперпозиции, т. е.

 (16.9)

18 вопрос.

Закон Био–Савара определяет вклад   в магнитную индукцию    результирующего магнитного поля, создаваемый малым участком Δl проводника с током I.



Здесь r – расстояние от данного участка Δl до точки наблюдения, α – угол между направлением на точку наблюдения и направлением тока на данном участке, μ₀ – магнитная постоянная. Направление вектора   определяется правилом буравчика: оно совпадает с направлением вращения рукоятки буравчика при его поступательном перемещении вдоль тока. Рис. 1.17.1 иллюстрирует закон Био–Савара на примере магнитного поля прямолинейного проводника с током. Если просуммировать (проинтегрировать) вклады в магнитное поле всех отдельных участков прямолинейного проводника с током, то получится формула для магнитной индукции поля прямого тока:

.

Рисунок 1.17.1. Иллюстрация закона Био–Савара

Закон Био–Савара позволяет рассчитывать магнитные поля токов различных конфигураций. Нетрудно, например, выполнить расчет магнитного поля в центре кругового витка с током. Этот расчет приводит к формуле



где R – радиус кругового проводника. Для определения направления вектора   также можно использовать правило буравчика, только теперь его рукоятку нужно вращать в направлении кругового тока, а поступательное перемещение буравчика укажет направление вектора магнитной индукции.

Рассмотрим некоторые примеры.

А. Магнитное поле прямолинейного проводника с током.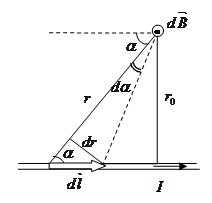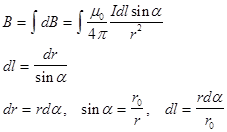

 



 

 

1) для проводника конечной длины:

 





 

2) для проводника бесконечной длины: a₁ = 0, a₂ = p

 

 .

 

Б. Магнитное поле в центре кругового тока: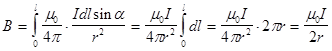



 



a=90⁰, sina=1, 

19 вопрос.

Потоком вектора магнитной индукции (магнитным потоком) (Ф) через площадку S называют скалярную величину равную:

(1),

где угол между и 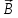, - нормаль к площадке S.

Ф равен количеству линий магнитной индукции, которые пересекают площадку S (рис.1). Поток магнитной индукции может быть положительным и отрицательным. Знак потока зависит от выбора положительного направлении нормали к площадке S.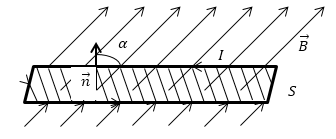

Рис.1

В том случае, если магнитное поле неоднородно, S не является плоской, то поверхность можно разбить на элементарные площадки dS, которые рассматриваются как плоские, а поле на этой площадке можно считать однородным. В таком случае магнитный поток (dФ) можно через такую поверхность определить, как:

(2).

Тогда полный поток через поверхность S находится как: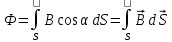

(3).

Основная единица измерения магнитного потока в системе СИ - вебер (Вб).

.

Теорема о циркуляции.

Циркуляцией вектора   называют сумму произведений  Δl, взятую по всему контуру L:



Теорема о циркуляции утверждает, что циркуляция вектора    магнитного поля постоянных токов по любому контуру L всегда равна произведению магнитной постоянной μ₀ на сумму всех токов, пронизывающих контур:



20 вопрос.

Для характеристики степени намагниченности вещества вводят понятие вектора намагниченности — векторную сумму магнитных моментов всех частиц, находящихся в единице объема вещества:

(1),

где суммирование проводится по магнитным моментам всех частиц (атомов, молекул), находящихся в объеме V. На основании (1) можно установить, что намагниченность измеряется в амперах на метр (А/м).

В таких же единицах выражена напряженность магнитного поля H. Между намагниченностью   и напряженностью  существует связь:

(2),

где — безразмерная величина, называемая магнитной восприимчивостью.

Из (2) видно, что магнитная восприимчивость численно равна намагниченности магнетика при единичной напряженности магнитного поля. Можно показать, что между магнитной восприимчивостью и магнитной проницаемостью существует связь:

(3).

По своему физическому содержанию формула (2) связывает поляризованность диэлектрика с напряженностью электрического поля   . Однако есть одно существенное отличие: диэлектрическая восприимчивость всегда положительна, в то время как магнитная восприимчивость может быть как положительной, так и отрицательной. Это означает, что поляризованность диэлектрика   всегда ориентирована в направлении поля   . В то же время намагниченность   может быть направлена как вдоль оси магнитного поля   , так и навстречу ему.

21 вопрос.



22 вопрос.

Диамагнетизм - свойство веществ намагничиваться навстречу приложенному магнитному полю.

Диамагнетиками называются вещества, магнитные моменты атомов которых в отсутствии внешнего поля равны нулю, т.к. магнитные моменты всех электронов атома взаимно скомпенсированы (например инертные газы, водород, азот, NaCl и др.).

При внесении диамагнитного вещества в магнитное поле его атомы приобретают наведенные магнитные моменты. В пределах малого объема ΔV изотропного диамагнетика наведенные магнитные моменты    всех атомов одинаковы и направлены противоположно вектору   .

Вектор намагниченности диамагнетика равен:

,

(6.4.2)

где n₀ – концентрация атомов,    – магнитная постоянная,    –магнитная восприимчивость среды.

Для всех диамагнетиков     Таким образом, вектор    магнитной индукции собственного магнитного поля, создаваемого диамагнетиком при его намагничивании во внешнем поле    направлен в сторону, противоположную   . (В отличие от диэлектрика в электрическом поле).

У диамагнетиков 

Парамагнетизм (от греч. para – возле, рядом и магнетизм) - свойство веществ во внешнем магнитном поле намагничиваться в направлении этого поля, поэтому внутри парамагнетика к действию внешнего поля прибавляется действие наведенного внутреннего поля.

Парамагнетиками называются вещества, атомы которых имеют, в отсутствие внешнего магнитного поля, отличный от нуля магнитный момент   .

Эти вещества намагничиваются в направлении вектора  .

К парамагнетикам относятся многие щелочные металлы, кислород   , оксид азота NO, хлорное железо    и др.

В отсутствие внешнего магнитного поля намагниченность парамагнетика   , так как векторы    разных атомов ориентированы беспорядочно.

При внесении парамагнетика во внешнее магнитное поле происходит преимущественная ориентация собственных магнитных моментов атомов     по направлению поля, так что парамагнетик намагничивается. Значения    для парамагнетиков положительны (   ) и находятся в пределах   , то есть примерно как и у диамагнетиков.

23 вопрос.

 К ферромагнетикам относятся вещества, магнитная восприимчивость которых положительна и достигает значений   . Намагниченность    и магнитная индукция    ферромагнетиков растут с увеличением напряженности магнитного поля    нелинейно, и в полях    намагниченность ферромагнетиков достигает предельного значения   , а вектор магнитной индукции растет линейно с   : 

Ферромагнетики –  это вещества, обладающие самопроизвольной намагниченностью, которая сильно изменяется под влиянием внешних воздействий – магнитного поля, деформации, температуры.

 Ферромагнетики, в отличие от слабо магнитных диа- и парамагнетиков, являются сильно магнитными веществами: внутреннее магнитное поле в них может в сотни раз превосходить внешнее поле.

Основные отличия магнитных свойств ферромагнетиков.

1. 
   Нелинейная зависимость намагниченности от напряженности магнитного поля Н (рис. 6.5).
   

Как видно из рис. 6.5, при    наблюдается магнитное насыщение.



Рис. 6.5

2. 
   При     зависимость магнитной индукции В от Н нелинейная, а при    – линейная (рис. 6.6).
   

Рис. 6.6

3. 
   Зависимость относительной магнитной проницаемости от Н имеет сложный характер (рис. 6.7), причем максимальные значения μ очень велики (   ).
   

Рис. 6.7

      

      5. Существование магнитного гистерезиса.

      На рисунке 6.10 показана петля гистерезиса – график зависимости намагниченности вещества от напряженности магнитного поля Н.



Рис. 6.10

      Намагниченность    при    называется намагниченностью насыщения.

      Намагниченность    при    называется остаточной намагниченностью (что необходимо для создания постоянных магнитов).

      Напряженность    магнитного поля, полностью размагниченного ферромагнетика, называется коэрцитивной силой. Она характеризует способность ферромагнетика сохранять намагниченное состояние.

24 вопрос.

Связь между напряженностью магнитного поля, индукцией и намагниченностью

В вакууме:

,

где H– напряженность магнитного поля, B– индукция магнитного поля, – магнитная постоянная.

В среде:

где I– вектор интенсивности намагничения среды (намагниченность) – векторная сумма магнитных моментов, находящихся в единице объема.

В изотропной среде:

где   – относительная магнитная проницаемость среды.

Граничные условия для вектора H

Пусть известно распределение напряженности электрического поля между краями щели. Если теперь взять пластинку, совпадающую по форме со щелью и считать, что магнитное поле на пластинке распределено так же, как электрическое между краями щели, то согласно принципу двойственности, электрическое поле в пространстве над экраном будет совпадать с магнитным полем вокруг пластинки, если граничные условия для вектора напряженности электрического и магнитного полей в обоих случаях совпадают. Граничным условием для вектора напряженности электрического поля на экране является требование обращения в нуль тангенциальной составляющей на нём. Отсюда следует совпадение структур электрического поля щели и магнитного поля пластинки, имеющей одинаковую форму со щелью.

Граничные условия для вектора B

Граничные условия для нормальных составляющих магнитного поля 

Обозначим векторные поля магнитной индукции соответственно изображению ниже в средах 1 и 2



В окрестности точки Р выделим цилиндрический объем с основаниями 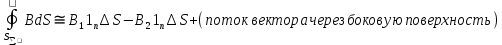и высотой образующей довольно небольшой, чтобы считать в пределах площадей постоянными. Следующим образом запишется через суммарную поверхность поток вектора магнитной индукции:

 

При стремлении 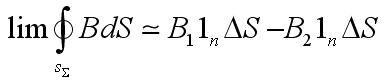 к нулю приближенное равенство становится точным. Если же к нулю устремить высоту цилиндра , то должным образом станет бесконечно малым поток вектора индукции сквозь боковую поверхность



От того, что справедлив во всех случаях закон неразрывности магнитных силовых линий сделаем запись 

или 

Следовательно, на границе раздела двух сред нормальные составляющие вектора магнитной индукции непрерывны. Поскольку 



записано крайнее соотношение может быть относительно магнитного поля относительно напряженностей: 



Исходя из этого видно, что на границе раздела в общем случае напряженность магнитного поля испытывает скачок.

25 вопрос.

Определение 1. При помещении в магнитное поле пластины-проводника или полупроводника под 90 °к направлению силовых линий магнитного потока произойдет перемещение электронов по поперечине пластины под действием силы Лоренца. Их направление зависит от того, в какую сторону идет сила тока и силовые линии магнитного потока. Иначе говоря, (ЭХ) эффект Холла – это частный случай действия силы Лоренца, то есть действия магнитного поля на заряженную частицу.

При изменении направления тока в пластине при помощи перемены местами проводников мы сможем наблюдать отклонение электронов вниз. Если направление не менять, а только лишь полюса магнитов, электроны начнут сдвигаться вниз. Когда применяются оба направления, сила Лоренца произведет их перемещение вверх.

Очевидно, что одна из кромок накапливает отрицательный заряд под действием силы Лоренца, на другая на противоположной стороне – положительный. Это говорит о наличии разности потенциалов между ними, то есть электрического напряжения. Увеличение этой разности будет происходить до тех пор, пока не уравновесит силу Лоренца.

Определение 2. Возникновение разности потенциалов в таких случаях, получило название напряжения Холла, которое можно рассчитать, используя формулу:

,

где I является силой тока, B – вектором магнитной индукции, e – зарядом электрона, p – количеством электронов в единице объема, t – толщиной пластины.