№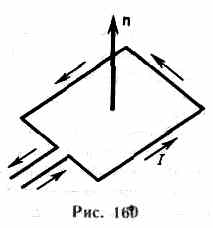 1магнитное взаимодействие постоянных токов. Вектор магнитной индукции. Закон Ампера. Закон Био-Савара-Лапласа. Магнитная индукция прямого и кругового тока.§ 109. Магнитное поле и его характеристикиОпыт показывает, что, подобно тому, как в пространстве, окружающем электрические заряды, возникает электростатическое поле, так в пространстве, окружающем токи и постоянные магниты, возникает силовое поле, называемое магнитным. Наличие магнитного поля обнаруживается по силовому действию на внесенные в него проводники с током или постоянные магниты. Особенноси магнитного поля:: действие только на движущиеся в эл. поле заряды. Опыт показывает, что характер воздействия магнитного поля на ток различен в зависимости от формы проводника, по которому течет ток, от расположения проводника и от направления тока. Следовательно, чтобы охарактеризовать магнитноеполе, надо рассмотреть его действие на определенный ток.Подобно тому, как при исследовании электростатического поля использовались точечные заряды, при исследовании магнитного поля используется замкнутый плоский контур с током (рамка с током), размеры которого малы по сравнению с расстоянием до токов, образующих магнитное поле. Ориентация контура в пространстве характеризуется направлением нормали к контуру. В качестве положительного направления нормали принимается направление, связанное с током правилом правого винта, т. е. за положительное направление нормали принимается направление поступательного движения винта, головка которого вращается в направлении тока, текущего в рамке (рис. 160). 1магнитное взаимодействие постоянных токов. Вектор магнитной индукции. Закон Ампера. Закон Био-Савара-Лапласа. Магнитная индукция прямого и кругового тока.§ 109. Магнитное поле и его характеристикиОпыт показывает, что, подобно тому, как в пространстве, окружающем электрические заряды, возникает электростатическое поле, так в пространстве, окружающем токи и постоянные магниты, возникает силовое поле, называемое магнитным. Наличие магнитного поля обнаруживается по силовому действию на внесенные в него проводники с током или постоянные магниты. Особенноси магнитного поля:: действие только на движущиеся в эл. поле заряды. Опыт показывает, что характер воздействия магнитного поля на ток различен в зависимости от формы проводника, по которому течет ток, от расположения проводника и от направления тока. Следовательно, чтобы охарактеризовать магнитноеполе, надо рассмотреть его действие на определенный ток.Подобно тому, как при исследовании электростатического поля использовались точечные заряды, при исследовании магнитного поля используется замкнутый плоский контур с током (рамка с током), размеры которого малы по сравнению с расстоянием до токов, образующих магнитное поле. Ориентация контура в пространстве характеризуется направлением нормали к контуру. В качестве положительного направления нормали принимается направление, связанное с током правилом правого винта, т. е. за положительное направление нормали принимается направление поступательного движения винта, головка которого вращается в направлении тока, текущего в рамке (рис. 160).
О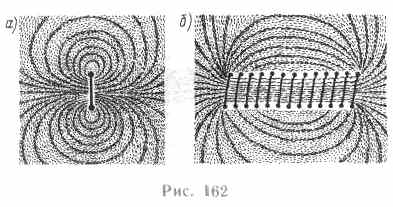 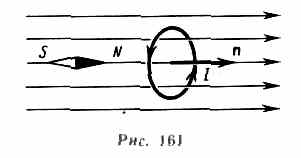 пыты показывают, что магнитное поле оказывает на рамку с током ориентирующее действие, поворачивая ее определенным образом. Этот результат связывается с определенным направлением магнитного поля. За направление магнитного поля в данной точке принимается направление, вдоль которого располагается положительная нормаль к рамке (рис. 161). За направление магнитного поля может быть также принято направление, совпадающее с направлением силы, которая действует на северный полюс магнитной стрелки, помещенной в данную точку. Так как оба полюса магнитной стрелки лежат в близких точках поля, то силы, действующие на оба полюса, равны друг другу. Следовательно, на магнитную стрелку действует пара сил, поворачивающая ее так, чтобы ось стрелки, соединяющая южный полюс с северным, совпадала с направлением поля.Рамкой с током можно воспользоваться также и для количественного описания магнитного поля. Так как рамка с током испытывает ориентирующее действие поля, то на нее в магнитном поле действует пара сил. Вращающий момент сил зависит как от свойств поля в данной точке, так и от свойств рамки: М=[рmВ], (109.1)где В — вектор магнитной индукции, являющейся количественной характеристикой магнитного поля, рm — вектор магнитного момента рамки с током. Для плоского контура с током Ipm = ISn, (109.2) где S — площадь поверхности контура (рамки), n—единичный вектор нормали к поверхности рамки. Направление рmсовпадает, таким образом, с направлением положительной нормали. Если в данную точку магнитного поля помещать рамки с различными магнитными моментами, то на них действуют различные вращающие моменты, однако отношение Mmax/pm (Мmax— максимальный вращающий момент) для всех контуров одно и то же и поэтому может служить характеристикой магнитного поля, называемой магнитной индукцией: В=Мmax/рm.Магнитная индукция в данной точке однородного магнитного поля определяется максимальным вращающим моментом, действующим на рамку с магнитным моментом, равным единице, когда нормаль к рамке перпендикулярна направлению поля. Следует отметить, что вектор В может быть выведен также из закона Ампера (см. §111) и из выражения для силы Лоренца (см. § 114).Так как магнитное поле является силовым, то его, по аналогии с электрическим, изображают с помощью линий магнитной индукции — линий, касательные к которым в каждой точке совпадают с направлением вектора В. Их направление задается правилом правого винта: головка винта, ввинчиваемого по направлению тока, вращается в направлении линий магнитной индукции. пыты показывают, что магнитное поле оказывает на рамку с током ориентирующее действие, поворачивая ее определенным образом. Этот результат связывается с определенным направлением магнитного поля. За направление магнитного поля в данной точке принимается направление, вдоль которого располагается положительная нормаль к рамке (рис. 161). За направление магнитного поля может быть также принято направление, совпадающее с направлением силы, которая действует на северный полюс магнитной стрелки, помещенной в данную точку. Так как оба полюса магнитной стрелки лежат в близких точках поля, то силы, действующие на оба полюса, равны друг другу. Следовательно, на магнитную стрелку действует пара сил, поворачивающая ее так, чтобы ось стрелки, соединяющая южный полюс с северным, совпадала с направлением поля.Рамкой с током можно воспользоваться также и для количественного описания магнитного поля. Так как рамка с током испытывает ориентирующее действие поля, то на нее в магнитном поле действует пара сил. Вращающий момент сил зависит как от свойств поля в данной точке, так и от свойств рамки: М=[рmВ], (109.1)где В — вектор магнитной индукции, являющейся количественной характеристикой магнитного поля, рm — вектор магнитного момента рамки с током. Для плоского контура с током Ipm = ISn, (109.2) где S — площадь поверхности контура (рамки), n—единичный вектор нормали к поверхности рамки. Направление рmсовпадает, таким образом, с направлением положительной нормали. Если в данную точку магнитного поля помещать рамки с различными магнитными моментами, то на них действуют различные вращающие моменты, однако отношение Mmax/pm (Мmax— максимальный вращающий момент) для всех контуров одно и то же и поэтому может служить характеристикой магнитного поля, называемой магнитной индукцией: В=Мmax/рm.Магнитная индукция в данной точке однородного магнитного поля определяется максимальным вращающим моментом, действующим на рамку с магнитным моментом, равным единице, когда нормаль к рамке перпендикулярна направлению поля. Следует отметить, что вектор В может быть выведен также из закона Ампера (см. §111) и из выражения для силы Лоренца (см. § 114).Так как магнитное поле является силовым, то его, по аналогии с электрическим, изображают с помощью линий магнитной индукции — линий, касательные к которым в каждой точке совпадают с направлением вектора В. Их направление задается правилом правого винта: головка винта, ввинчиваемого по направлению тока, вращается в направлении линий магнитной индукции.
Линии магнитной индукции можно «проявить» с помощью железных опилок, намагничивающихся в исследуемом поле и ведущих себя подобно маленьким магнитным стрелкам. На рис. 162, а показаны линии магнитной индукции поля кругового тока, на рис. 162, б — линии магнитной индукции поля соленоида (соленоид — равномерно намотанная на цилиндрическую поверхность проволочная спираль, по которой течет электрический ток).
Линии магнитной индукции всегда замкнуты и охватывают проводники с током. Этим они отличаются от линий напряженности электростатического поля, которые являются разомкнутыми (начинаются на положительных зарядах и кончаются на отрицательных).
В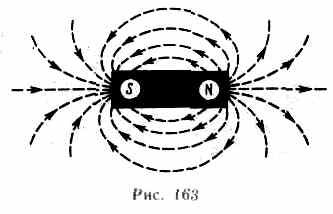 ектор магнитной индукции В характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками, т. е. при одном и том же токе и прочих равных условиях вектор В в различных средах будет иметь разные значения. ектор магнитной индукции В характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками, т. е. при одном и том же токе и прочих равных условиях вектор В в различных средах будет иметь разные значения.
М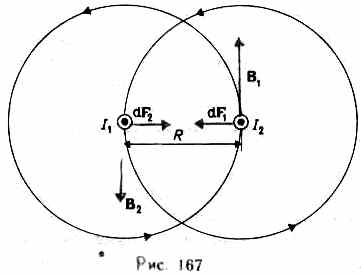 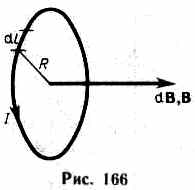 агнитное поле макротоков описывается вектором напряженности Н. Для однородной изотропной среды вектор магнитной индукции связан с вектором напряженности следующим соотношением:В=0Н, (109.3)где 0 — магнитная постоянная, — безразмерная величина — магнитная проницаемость среды, показывающая, во сколько раз магнитное поле макротоков Н усиливается за счет поля микротоков среды. Сравнивая векторные характеристики электростатического (Е и D) и магнитного (В и Н) полей, укажем, что аналогом вектора напряженности электростатического поля Е является вектор магнитной индукции В, так как векторы Е и В определяют силовые действия этих полей и зависят от свойств среды. Аналогом вектора электрического смещения D является вектор напряженности Н магнитного поля.§ 110. Закон Био — Савара — Лапласа и его применение к расчету магнитного поля агнитное поле макротоков описывается вектором напряженности Н. Для однородной изотропной среды вектор магнитной индукции связан с вектором напряженности следующим соотношением:В=0Н, (109.3)где 0 — магнитная постоянная, — безразмерная величина — магнитная проницаемость среды, показывающая, во сколько раз магнитное поле макротоков Н усиливается за счет поля микротоков среды. Сравнивая векторные характеристики электростатического (Е и D) и магнитного (В и Н) полей, укажем, что аналогом вектора напряженности электростатического поля Е является вектор магнитной индукции В, так как векторы Е и В определяют силовые действия этих полей и зависят от свойств среды. Аналогом вектора электрического смещения D является вектор напряженности Н магнитного поля.§ 110. Закон Био — Савара — Лапласа и его применение к расчету магнитного поля 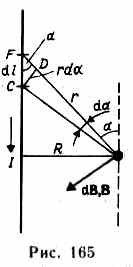 Закон Био — Савара — Лапласа для проводника с током I, элемент которого dlсоздает в некоторой точке А (рис. 164) индукцию поля dB, записывается в виде Закон Био — Савара — Лапласа для проводника с током I, элемент которого dlсоздает в некоторой точке А (рис. 164) индукцию поля dB, записывается в виде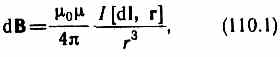 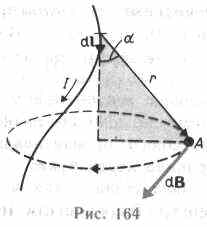 где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r — радиус-вектор, проведенный из элемента dl проводника в точку А поля, r— модуль радиуса-вектора г. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление dB, если поступательное движение винта соответствует направлению тока в элементе. Модуль вектора dB определяется выражением где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r — радиус-вектор, проведенный из элемента dl проводника в точку А поля, r— модуль радиуса-вектора г. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление dB, если поступательное движение винта соответствует направлению тока в элементе. Модуль вектора dB определяется выражением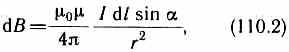 где а — угол между векторами dl и г. Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности: где а — угол между векторами dl и г. Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности: Расчет характеристик магнитного поля (В и Н) по приведенным формулам в общем случае довольно сложен. Однако если распределение тока имеет определенную симметрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции позволяет довольно просто рассчитать конкретные поля. Рассмотрим два примера.1. Магнитное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол а (угол между векторами dl и r), выразив через него все остальные величины. Из рис. 165 следует, что Расчет характеристик магнитного поля (В и Н) по приведенным формулам в общем случае довольно сложен. Однако если распределение тока имеет определенную симметрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции позволяет довольно просто рассчитать конкретные поля. Рассмотрим два примера.1. Магнитное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол а (угол между векторами dl и r), выразив через него все остальные величины. Из рис. 165 следует, что 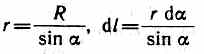 (радиус дуги CDвследствие малости dlравен r, и угол FDCпо этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна (радиус дуги CDвследствие малости dlравен r, и угол FDCпо этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна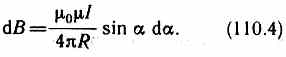 Так как угол а для всех элементов прямого тока изменяется в пределах от 0 до я, то, согласно (110.3) и (110.4), Так как угол а для всех элементов прямого тока изменяется в пределах от 0 до я, то, согласно (110.3) и (110.4),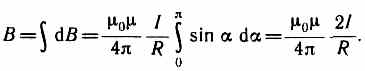 Следовательно, магнитная индукция поля прямого тока Следовательно, магнитная индукция поля прямого тока 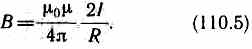 2. Магнитное поле в центре кругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитное поле одинакового направления — вдоль нормали от витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sin=1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2), 2. Магнитное поле в центре кругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитное поле одинакового направления — вдоль нормали от витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sin=1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2), 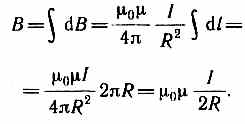 Тогда Тогда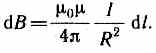 Следовательно, магнитная индукция поля в центре кругового проводника с током Следовательно, магнитная индукция поля в центре кругового проводника с током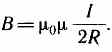 § 111. Закон Ампера. Взаимодействие параллельных токов.Магнитное поле (см. § 109) оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в прводнике и векторному произведению элемента длиной dl проводника на магнитную индукцию В:dF = I[dl, В]. (111.1) Направление вектора dF может быть найдено, согласно (111.1), по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток. Модуль силы Ампера (см. (111.1)) вычисляется по формулеdF = IBdlsin, (111.2) где a — угол между векторами dl и В. § 111. Закон Ампера. Взаимодействие параллельных токов.Магнитное поле (см. § 109) оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в прводнике и векторному произведению элемента длиной dl проводника на магнитную индукцию В:dF = I[dl, В]. (111.1) Направление вектора dF может быть найдено, согласно (111.1), по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток. Модуль силы Ампера (см. (111.1)) вычисляется по формулеdF = IBdlsin, (111.2) где a — угол между векторами dl и В.
Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I1и I2 (направления токов указаны на рис. 167), расстояние между которыми равно R. Каждый из проводников создает магнитное поле, которое действует по закону Ампера на другой проводник с током. Рассмотрим, с какой силой действует магнитное поле тока I1 на элемент dl второго проводника с током I2. Ток I1 создает вокруг себя магнитное поле, линии магнитной индукции которого представляют собой концентрические окружности. Направление вектора b1 задается правилом правого винта, его модуль по формуле (110.5) равен 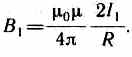 Направление силы dF1, с которой поле B1 действует на участок dl второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, согласно (111.2), с учетом того, что угол между элементами тока I2 и вектором B1 прямой, равен dF1=I2B1dl, или, подставляя значение для В1, получим Направление силы dF1, с которой поле B1 действует на участок dl второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, согласно (111.2), с учетом того, что угол между элементами тока I2 и вектором B1 прямой, равен dF1=I2B1dl, или, подставляя значение для В1, получим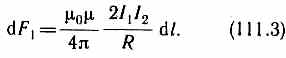 Рассуждая аналогично, можно показать, что сила dF2, с которой магнитное поле тока I2 действует на элемент dl первого проводника с током I1, направлена в противоположную сторону и по модулю равна Рассуждая аналогично, можно показать, что сила dF2, с которой магнитное поле тока I2 действует на элемент dl первого проводника с током I1, направлена в противоположную сторону и по модулю равна 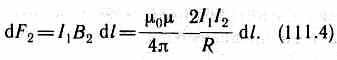 Сравнение выражений (111.3) и (111.4) показывает, чтоdF1=dF2, т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой Сравнение выражений (111.3) и (111.4) показывает, чтоdF1=dF2, т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой 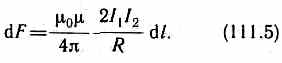 Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая формулой (111.5). §112.Магнитная постоянная. Единицы магнитной индукции и напряженности магнитного поля Если два параллельных проводника с током находятся в вакууме (=1), то сила взаимодействия на единицу длины проводника, согласно (111.5), равна Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая формулой (111.5). §112.Магнитная постоянная. Единицы магнитной индукции и напряженности магнитного поля Если два параллельных проводника с током находятся в вакууме (=1), то сила взаимодействия на единицу длины проводника, согласно (111.5), равна 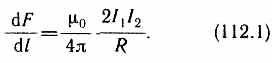 Для нахождения числового значения 0 воспользуемся определением ампера, согласно которому при I1=I2=1А и R=1 м dF/dl=2•10-7 Н/м. Подставив это значение в формулу (112.1), получим 0=4•10-7 Н/А2=4•10-7 Гн/м, где генри (Гн) — единица индуктивности (см. §126). Закон Ампера позволяет определить единицу магнитной индукции В. Предположим, что элемент проводника dl с током I перпендикулярен направлению магнитного поля. Тогда закон Ампера (см. (111.2)) запишется в виде dF=IBdl, откуда Для нахождения числового значения 0 воспользуемся определением ампера, согласно которому при I1=I2=1А и R=1 м dF/dl=2•10-7 Н/м. Подставив это значение в формулу (112.1), получим 0=4•10-7 Н/А2=4•10-7 Гн/м, где генри (Гн) — единица индуктивности (см. §126). Закон Ампера позволяет определить единицу магнитной индукции В. Предположим, что элемент проводника dl с током I перпендикулярен направлению магнитного поля. Тогда закон Ампера (см. (111.2)) запишется в виде dF=IBdl, откуда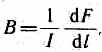 Единица магнитной индукции — тесла (Тл): 1 Тл—магнитная индукция такого однородного магнитного поля, которое действует с силой в 1 Н на каждый метр длины прямолинейного проводника, расположенного перпендикулярно направлению поля, если по этому проводнику проходит ток в 1 А:1Тл=1Н/(А•м). Так как 0= 4•10-7 Н/А2, а в случае вакуума (=1), согласно (1.09.3), В =0H, то для данного случая H=В/0. Единица напряженности магнитного поля — ампер на метр (А/м): 1 А/м — напряженность такого поля, магнитная индукция которого в вакууме равна 4•10-7 Тл. Единица магнитной индукции — тесла (Тл): 1 Тл—магнитная индукция такого однородного магнитного поля, которое действует с силой в 1 Н на каждый метр длины прямолинейного проводника, расположенного перпендикулярно направлению поля, если по этому проводнику проходит ток в 1 А:1Тл=1Н/(А•м). Так как 0= 4•10-7 Н/А2, а в случае вакуума (=1), согласно (1.09.3), В =0H, то для данного случая H=В/0. Единица напряженности магнитного поля — ампер на метр (А/м): 1 А/м — напряженность такого поля, магнитная индукция которого в вакууме равна 4•10-7 Тл.
№2 Тепловое излучение. Спектральные характеристики теплового излучения. Закон Кирхгофа. Абсолютно черное тело. Законы Стефана-Больцмана и Вина. Формула Рэлея-Джинса и «ультрафиолетовая катастрофа». 197. Тепловое излучение и Его характеристики Тела, нагретые до достаточно высоких температур, светятся. Свечение тел, обусловленное нагреванием, называется тепловым (температурным) излучением. Тепловое излучение характеризуется сплошным спектром, положение максимума которого зависит от температуры. При высоких температурах излучаются короткие (видимые и ультрафиолетовые) электромагнитные волны, при низких - преимущественно длинные (инфракрасные). Тепловое излучение - практически единственный вид излучения, который может быть равновесным. Количественной характеристикой теплового излучения служит спектральная плотность энергетической светимости (излучательностн) тела - мощность излучения с единицы площади поверхности тела в интервале частот единичной ширины: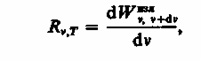 где dWизлv, dv - энергия электромагнитного излучения, испускаемого за единицу времени (мощность излучения) с единицы площади поверхности тела в интервале частот от v до v+dv.Единица спектральной плотности энергетической светимости (Rv,T)- джоуль на метр в квадрате (Дж/м2).Записанную формулу можно представить в виде функции длины волны: где dWизлv, dv - энергия электромагнитного излучения, испускаемого за единицу времени (мощность излучения) с единицы площади поверхности тела в интервале частот от v до v+dv.Единица спектральной плотности энергетической светимости (Rv,T)- джоуль на метр в квадрате (Дж/м2).Записанную формулу можно представить в виде функции длины волны: 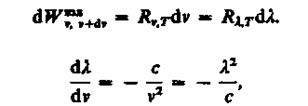 где знак минус указывает на то, что с возрастанием одной из величин (V или l) другая величина убывает. Поэтому в дальнейшем знак минус будем опускать. Таким образом, где знак минус указывает на то, что с возрастанием одной из величин (V или l) другая величина убывает. Поэтому в дальнейшем знак минус будем опускать. Таким образом,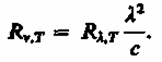 (197.1)С помощью формулы (197.1) можно перейти от Rv,T к Rl,T, и наоборот.Зная спектральную плотность энергетической светимости, можно вычислить интегральную энергетическую светимость (интегральную нзлучательность) (ее называют про сто энергетической светимостью тела), просуммировав по всем частотам: (197.2)Способность тел поглощать падающее на них излучение характеризуется спектральной поглощательной способностью (197.1)С помощью формулы (197.1) можно перейти от Rv,T к Rl,T, и наоборот.Зная спектральную плотность энергетической светимости, можно вычислить интегральную энергетическую светимость (интегральную нзлучательность) (ее называют про сто энергетической светимостью тела), просуммировав по всем частотам: (197.2)Способность тел поглощать падающее на них излучение характеризуется спектральной поглощательной способностью 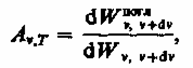
показывающей, какая доля энергии, приносимой за единицу времени на единицу площади поверхности тела падающими на нее электромагнитными волнами с частота ми от v до v+dv, поглощается телом. Спектральная поглощательная способность - величина безразмерная. Величины Rv,Tи Аv,Tзависят от природы тела, его термодинамической температуры и при этом различаются для излучений с различными частотами. Поэтому эти величины относят к определенным Т иv (вернее, к достаточно узкому интервалу частот от v до v+dv).
Тело, способное поглощать полностью при любой температуре все падающее на него излучение любой частоты, называется черным. Следовательно, спектральная поглощательная способность черного тела для всех частот и температур тождественно равна единице (Ачv,T = 1). Абсолютно черных тел в природе нет, однако такие тела, как сажа, платиновая чернь, черный бархат и некоторые другие, в определенном интервале частот по своим свойствам близки к ним.
Идеальной моделью черного тела является замкнутая полость с небольшим отверстием О, внутренняя поверхность которой зачернена (рис. 286). Луч света, попавший внутрь такой полости, испытывает многократные отражения от стенок, в результате чего интенсивность вышедшего излучения оказывается практически равной нулю. Опыт показывает, что при размере отверстия, меньшего 0,1 диаметра полости, падающее излучение всех частот полностью поглощается. Вследствие этого открытые окна домов со стороны улицы кажутся черными, хотя внутри комнат достаточно светло из-за отражения света от стен.
Наряду с понятием черного тела используют понятие серого тела - тела, поглощательная способность которого меньше единицы, но одинакова для всех частот и зависит только от температуры, материала и состояния поверхности тела. Таким образом, дня серого тела Асv,T = АТ =const <1.
И сследование теплового излучения сыграло важную роль в создании квантовой теории света, поэтому необходимо рассмотреть законы, которым оно подчиняется. сследование теплового излучения сыграло важную роль в создании квантовой теории света, поэтому необходимо рассмотреть законы, которым оно подчиняется.
|
 Скачать 2.54 Mb.
Скачать 2.54 Mb. агнитное поле макротоков описывается вектором напряженности Н. Для однородной изотропной среды вектор магнитной индукции связан с вектором напряженности следующим соотношением:В=0Н, (109.3)где 0 — магнитная постоянная, — безразмерная величина — магнитная проницаемость среды, показывающая, во сколько раз магнитное поле макротоков Н усиливается за счет поля микротоков среды. Сравнивая векторные характеристики электростатического (Е и D) и магнитного (В и Н) полей, укажем, что аналогом вектора напряженности электростатического поля Е является вектор магнитной индукции В, так как векторы Е и В определяют силовые действия этих полей и зависят от свойств среды. Аналогом вектора электрического смещения D является вектор напряженности Н магнитного поля.§ 110. Закон Био — Савара — Лапласа и его применение к расчету магнитного поля
агнитное поле макротоков описывается вектором напряженности Н. Для однородной изотропной среды вектор магнитной индукции связан с вектором напряженности следующим соотношением:В=0Н, (109.3)где 0 — магнитная постоянная, — безразмерная величина — магнитная проницаемость среды, показывающая, во сколько раз магнитное поле макротоков Н усиливается за счет поля микротоков среды. Сравнивая векторные характеристики электростатического (Е и D) и магнитного (В и Н) полей, укажем, что аналогом вектора напряженности электростатического поля Е является вектор магнитной индукции В, так как векторы Е и В определяют силовые действия этих полей и зависят от свойств среды. Аналогом вектора электрического смещения D является вектор напряженности Н магнитного поля.§ 110. Закон Био — Савара — Лапласа и его применение к расчету магнитного поля  сследование теплового излучения сыграло важную роль в создании квантовой теории света, поэтому необходимо рассмотреть законы, которым оно подчиняется.
сследование теплового излучения сыграло важную роль в создании квантовой теории света, поэтому необходимо рассмотреть законы, которым оно подчиняется.