Закон Ампера. Закон БиоСавараЛапласа. Магнитная индукция прямого и кругового тока

• Название: Закон Ампера. Закон БиоСавараЛапласа. Магнитная индукция прямого и кругового тока
• Анкор: shpora.doc
• Дата: 27.02.2017
• Размер: 2.54 Mb.
• Имя файла: shpora.doc
• Тип: Закон; #3177
• страница: 4 из 12

§ 205. Масса и импульс фотона. Давление светаСогласно гипотезе световых квантов Эйнштейна, свет испускается, поглощается и распространяется дискретными порциями (квантами), названными фотонами. Энергия фотона E₀=hv. Его масса находится из закона взаимосвязи массы и энергии (см. (40.8)):                  (205.1) Фотон - элементарная частица, которая всегда (в любой среде!) движется со скоростью света с и имеет массу покоя, равную нулю. Следовательно, масса фотона отличается от массы таких элементарных частиц, как электрон, протон и нейтрон, которые обладают отличной от нуля массой покоя и могут находиться в состоянии покоя.Импульс фотона р_g получим, если в общей формуле (40.7) теории относительности положим массу покоя фотонаm_0g = 0:                     (205.2)Из приведенных рассуждений следует, что фотон, как и любая другая частица, характеризуется энергией, массой и импульсом. Выражения (205.1), (205.2) и (200.2) связывают корпускулярные характеристики фотона - массу, импульс и энергию - с волновой характеристикой света - его частотой v.

Если фотоны обладают импульсом, то свет, падающий на тело, должен оказывать на него давление. Согласно квантовой теории, давление света на поверхность обусловлено тем, что каждый фотон при соударении с поверхностью передает ей свой импульс.

Рассчитаем с точки зрения квантовой теории световое давление, оказываемое на поверхность тела потоком монохроматического излучения (частота v), падающего перпендикулярно поверхности. Если в единицу времени на единицу площади поверхности тела падает N фотонов, то при коэффициенте отражения rсвета от поверхности тела rNфотонов отразится, a (l - r)N- поглотится. Каждый поглощенный фотон передает поверхности импульс р_g = hv/c, а каждый отраженный - 2 р_g = 2hv/c (при отражении импульс фотона изменяется на - р_g). Давление света на поверхность равно импульсу, который передают поверхности в 1 с N фотонов:

 Nhv = E_eесть энергия всех фотонов, падающих на единицу поверхности в единицу времени, т.e. энергетическая освещенность поверхности (см. § 168), a

E_e/c = w- объемная плотность энергии излучения. Поэтому давление, производимое светом при нормальном падении на поверхность,                       (205.3)

Формула (205.3), выведенная на основе квантовых представлений, совпадает с выражением, получаемым из электромагнитной (волновой) теории Максвелла (см. § 163). Таким образом, давление света одинаково успешно объясняется и волновой, и квантовой теорией. Как уже говорилось (см. § 163), экспериментальное доказательство существования светового давления на твердые тела и газы дано в опытах П. Н. Лебедева, сыгравших в свое время большую роль в утверждении теории Максвелла. Лебедев использовал легкий подвес на тонкой нити, по краям которого прикреплены легкие крылышки, одни из которых зачернены, а поверхности других зеркальные. Для исключения конвекции и радиометрического эффекта (см. § 49) использовалась подвижная система зеркал, позволяющая направлять свет на обе поверхности крылышек, подвес помещался в откачанный баллон, крылышки подбирались очень тонкими (чтобы температура обеих поверхностей была одинакова). Световое давление на крылышки определялось по углу закручивания нити подвеса и совпадало с теоретически рассчитанным. В частности оказалось, что давление света на зеркальную поверхность вдвое больше, чем на зачерненную (см. (205.3)).

 

§ 206. Эффект Комптона и его элементарная теория

 

Наиболее полно корпускулярные свойства света проявляются в эффекте Комптона. Американский физик А. Комптон (1892-1962), исследуя в 1923 г. рассеяние монохроматического рентгеновского излучения веществами с легкими атомами (парафин, бор), обнаружил, что в составе рассеянного излучения наряду с излучением первоначальной длины волны наблюдается также более длинноволновое излучение. Опыты показали, что разность ДЯ=Я'-Я не зависит от длины волны Я падающего излучения и природы рассеивающего вещества, а определяется только углом рассеяния                     (206.1)

 где l¢ - длина волны рассеянного излучения, l_C - комптоновская длина волны (при рассеянии фотона на электронеl_C =2,426 пм).

 Эффектом Комптона называется упругое рассеяние коротковолнового электромагнитного излучения (рентгеновского и g-излучений) на свободных (или слабосвязанных) электронах вещества, сопровождающееся увеличением длины волны. Этот эффект не укладывается в рамки волновой теории, согласно которой длина волны при рассеянии изменяться не должна: под действием периодического поля световой волны электрон колеблется с частотой поля и поэтому излучает рассеянные волны той же частоты.

Объяснение эффекта Комптона дано на основе квантовых представлений о природе света. Если считать, как это делает квантовая теория, что излучение имеет корпускулярную природу, т. е. представляет собой поток фотонов, то эффект Комптона - результат упругого столкновения рентгеновских фотонов со свободными электронами вещества (для легких атомов электроны слабо связаны с ядрами атомов, поэтому их можно считать свободными). В процессе этого столкновения фотон передает электрону часть своих энергии и импульса в соответствии с законами их сохранения.

Рассмотрим упругое столкновение двух частиц (рис. 291) - налетающего фотона, обладающего импульсом р_g = hv/cи энергией e_g = hv, с покоящимся свободным электроном (энергия покоя W₀ = m₀c²; m₀- масса покоя электрона). Фотон, столкнувшись с электроном, передает ему часть своей энергии и импульса и изменяет направление движения (рассеивается). Уменьшение энергии фотона означает увеличение длины волны рассеянного излучения. При каждом столкновении выполняются законы со хранения энергии и импульса.Согласно закону сохранения энергии,         (206.2) а согласно закону сохранения импульса

 где W₀ = m₀c²-энергия электрона до столкновения, e_g = hv - энергия налетающего фотона,   - энергия электрона после столкновения (используется релятивистская формула, так как скорость электрона отдачи в общем случае значительна), e_r=Av' - энергия рассеянного фотона. Подставив в выражение (206.2) значения величин и представив (206.3) в соответствии с рис. 291, получим                   (206.4) (206.5)

 

Рис. 291 Решая уравнения (206.4) и (206.5) совместно, получим

 Поскольку v = c/l, v'=c/l' и Dl = l'-l, получим

Выражение (206.6) есть не что иное, как полученная экспериментально Комптоном формула (206.1). Подстановка в нее значений h, m₀ и сдает комптоновскую длину волны электрона l_C = h/(m_Cс)= 2,426 им.

Наличие в составе рассеянного излучения несмещенной линии (излучения первоначальной длины волны) можно обменить следующим образом. При рассмотрении механизма рассеяния предполагалось, что фотон соударяется лишь со свободным электроном. Однако если электрон сильно связан с атомом, как это имеет место для внутренних электронов (особенно в тяжелых атомах), то фотон обменивается энергией и импульсом с атомом в целом. Так как масса атома по сравнению с массой электрона очень велика, то атому передается лишь ничтожная часть энергии фотона. Поэтому в данном случае длина волны l' рассеянного излучения практически не будет отличаться от длины волны l падающего излучения.

Из приведенных рассуждений следует также, что эффект Комптона не может наблюдаться в видимой области спектра, поскольку энергия фотона видимого света сравнима с энергией связи электрона с атомом, при этом даже внешний электрон нельзя считать свободным.

Эффект Комптона наблюдается не только на электронах, но и на других заряженных частицах, например протонах, однако из-за большой массы протона его отдача «просматривается» лишь при рассеянии фотонов очень высоких энергий.

Как эффект Комптона, так и фотоэффект на основе квантовых представлении обусловлены взаимодействием фотонов с электронами. В первом случае фотон рассеивается, во втором - поглощается. Рассеяние происходит при взаимодействии фотона со свободным электроном, а фотоэффект - со связанными электронами. Можно показать что при столкновении фотона со свободным электроном не может произойти поглощения фотона, так как это находится в противоречии с законами сохранения импульса и энергии. Поэтому при взаимодействии фотонов со свободными электрона-ми может наблюдаться только их рассеяние, т. е. эффект Комптона.

 

§ 207. Единство корпускулярных и волновых свойств электромагнитного излучения

Рассмотренные в этой главе явления - излучение черного тела, фотоэффект, эффект Комптона - служат доказательством квантовых (корпускулярных) представлении о свете как о потоке фотонов. С другой стороны, такие явления, как интерференция, дифракция и поляризация света, убедительно подтверждают волновую (электромагнитную) природу света. Наконец, давление и преломление света объясняются как волновой так и квантовой теориями. Таким образом, электромагнитное излучение обнаруживает удивительное единство, казалось бы, взаимоисключающих свойств -непрерывных (волны) и дискретных (фотоны), которые взаимно дополняют друг друга. Основные уравнения (см. § 205), связывающие корпускулярные свойства электромагнитного излучения (энергия и импульс фотона) с волновыми свойствами (частота или длина волны):Более детальное рассмотрение оптических явлений приводит к выводу, что свойства непрерывности, характерные для электромагнитного поля световой волны, не следует противопоставлять свойствам дискретности, характерным для фотонов. Свет, обладая одновременно корпускулярными и волновыми свойствами, обнаруживает определенные закономерности в их проявлении. Так, волновые свойства света проявляются в закономерностях его распространения, интерференции, дифракции, поляризации, а корпускулярные - в процессах взаимодействия света с веществом. Чем больше длина волны, тем меньше энергия и импульс фотона и тем труднее обнаруживаются квантовые свойства света (с этим связано, например, существование красной границы фотоэффекта). Наоборот, чем меньше длина волны, тем больше энергия и импульс фотона и тем труднее обнаруживаются волновые свойства света (например, волновые свойства (дифракция) рентгеновского излучения обнаружены лишь после применения в качестве дифракционной решетки кристаллов).

Взаимосвязь между двойственными корпускулярно-волновыми свойствами света можно объяснить, если использовать, как это делает квантовая оптика, статистический подход к рассмотрению закономерностей распространения света. Например, дифракция света на щели состоит в том, что при прохождении света через щель происходит перераспределение фотонов в пространстве. Так как вероятность попадания фотонов в различные точки экрана неодинакова, то и возникает дифракционная картина. Освещенность экрана пропорциональна вероятности попадания фотонов на единицу площади экрана. С другой стороны, по волновой теории, освещенность пропорциональна квадрату амплитуды световой волны в той же точке экрана. Следовательно, квадрат амплитуды световой волны в данной точке пространства является мерой вероятности попадания фотонов в данную точку

№7.классификация магнетиков: диамагнетики, парамагнетики, ферромагнетики, антиферромагнетики и ферримагнетики.Классификация магнетиковВсе существующие в природе вещества по своим магнитным свойствам подразделяются на пять видов магнетиков: диамагнетики, парамагнетики, ферромагнетики, антиферромагнетики и ферримагнетики (ферриты). В связи с тем что магнитную активность проявляют все вещества без исключения, можно утверждать, что магнитные свойства веществ определяются элементарными частицами, входящими в состав каждого атома. Такими одинаковыми для всех веществ частицами являются электроны, протоны и нейтроны. Исследования показали, что магнитные моменты протона и нейтрона почти на три порядка ниже наименьшего магнитного момента электрона, поэтому в первом приближении можно пренебречь магнитным моментом ядра, состоящего из протонов и нейтронов, и полагать, что магнитные свойства атома в целом определяются электронами. Это положение является фундаментальным в электронной теории магнетизма, которая общепринята в учении о магнетизме.Каждый атом вещества представляет собой динамическую систему, состоящую из ядра и электронного облака. Каждый электрон обладает определенным спиновым магнитным моментом  и орбитальным магнитным моментом . С некоторой степенью упрощения можно сказать, что спиновый магнитный момент обусловлен вращением электрона вокруг собственной оси, а орбитальный − движением электрона по некоторой замкнутой орбите внутри атома. Следовательно, полный магнитный момент атома будет представлять собой геометрическую сумму орбитальных и спиновых магнитных моментов электронов, относящихся к данному атому

где z − число электронов в атоме.

Рассмотрим макроскопические характеристики твердых тел, связанные с характером взаимодействия магнитных моментов с внешним полем и определяющие принадлежность данного вещества к одному из видов магнетиков [38]В любом веществе, внесенном в магнитное поле, возникает суммарный магнитный момент , который складывается из сумм магнитных моментов , связанных с отдельными частицами (атомами, молекулами). Размерность магнитного момента в системе «СИ» − Вольтсекундаметр [Всм] или Веберметр [Вбм].Одна из основных характеристик магнетиков – их намагниченность Намагниченность j − векторная величина, модуль которой равен магнитному моменту единицы объема вещества. Намагниченность растет с ростом индукции магнитного поля  (или напряженности ) в соответствии с законом

где − магнитная постоянная,  − относительная магнитная проницаемость, которая показывает, во сколько раз магнитная индукция поля в данной среде больше или меньше, чем в вакууме (в вакууме  = 1), æ − магнитная восприимчивость вещества, характеризующая способность данного вещества намагничиваться полем напряженности .

Величины æ и  являются скалярными, и магнитная восприимчивость æ для различных веществ может принимать значения как больше, так и меньше нуля. Руководствуясь этим свойством, вещества можно разделить на пара-, диа- и ферромагнетики.

Если магнитная восприимчивость принимает положительные значения (æ > 0), то вектор намагниченности (из формулы 7.4)  сонаправлен вектору напряженности внешнего магнитного поля  (). Такие вещества относятся к парамагнетикам.

Если магнитная восприимчивость æ < 0, то векторы намагниченности и напряженности направлены противоположно друг другу (), что характерно для диамагнетиков.

Как правило, по абсолютной величине магнитная восприимчивость парамагнетиков больше, чем диамагнетиков. Зависимость намагниченности этих типов магнетиков от величины напряженности магнитного поля   линейна (рис. 7.1), и при отсутствии внешнего поля она равна нулю.

Интересно, что линейная зависимость  для парамагнетиков имеет место только в области слабых полей и высоких температур. В сильных полях и при низких температурах  выходит на насыщение (рис. 7.2). 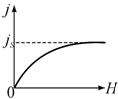Рис. 7.1. Зависимость намагниченности от напряженности магнитного поля: 1диамагнетика; 2  парамагнетика Рис. 7.2. Зависимость намагниченности от напряженности магнитного поля в сильных полях и при низких температурах выходит на насыщение 

К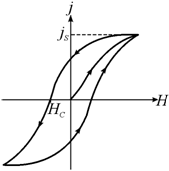роме двух рассмотренных видов магнетиков, имеется также достаточно большая группа веществ, обладающих спонтанной намагниченностью. Они называются ферромагнетиками и имеют отличную от нуля магнитную восприимчивость  () даже в отсутствие внешнего поля. Механизм намагничивания ферромагнетиков оказывается довольно сложным, и полный цикл намагниченности ферромагнетиков описывается петлей гистерезиса (рис. 7.3).В ряде кристаллов направления вектора магнитной индукции и напряженности магнитного поля  не совпадают. В этом случае магнитная проницаемость вещества является тензорной величиной, т. е. зависит от направления внутри кристалла. Такие вещества называются магнитно-анизотропными. Мы будем рассматривать здесь только магнитно-изотропные вещества, для которых магнитная проницаемость − простое число.

Найдем связь между магнитной проницаемостью и восприимчивостью вещества. Величина магнитной индукции  связана с напряженностью поля  соотношением

  

Для ферромагнетика результирующее поле в нем, которое и является магнитной индукцией, можно определить как

:

(7.6)

поле в ферромагнетике складывается из напряженности внешнего магнитного поля  и намагниченности , создающей внутреннее магнитное поле. Тогда из формул (7.6), (7.5) и

(7.4) получим = >

Выше было сказано, что магнитный момент атомов связан с движением электронов относительно своей оси и их орбитальным движением. Следовательно, существует некая жесткая связь между механическими и магнитными характеристиками атомов. Эта связь задается так называемыми гиромагнитными соотношениями. Обозначим орбитальный механический момент электрона , а спиновый механический момент электрона . Пользуясь обозначениями магнитных моментов, заданными в формуле (7.1), запишем гиромагнитные соотношения где е − заряд электрона, а т − его масса.

Следуя первому постулату Бора, согласно которому орбитальный момент количества движения электрона  должен быть квантован и кратен величине  (постоянной Планка, деленной на 2π), можно сделать вывод, что квантован и орбитальный магнитный момент  . Элементарный магнитный момент атома с одним электроном, движущимся по первой орбитали, называется магнетоном Бора:

.Диамагнетики – вещества, характеризуемые отрицательным значением магнитной восприимчивости χ. Вследствие этого вектор намагничивания  в этих веществах направлен противоположно внешнему намагничивающему полю . Диамагнетиками являются, например, вода (χ = - 9∙10^-6), серебро (χ = - 2,6∙10^-5), висмут (χ = - 1,7∙10^-4).Парамагнетики – характеризуются положительным значение χ , ведут они себя подобно диэлектрикам с диэлектрической проницаемостью ε>1, то есть вектор в этих веществах параллелен намагничивающему полю . К парамагнетикам относятся алюминий (χ = 2,1∙10^-6), платина (χ = 3∙10^-4), хлористое железо (χ = 2,5∙10^-3).

Ферромагнетики – особый вид магнетиков, отличающийся от других магнетиков следующими характерными признаками: 1) высоким значением магнитной восприимчивости (см. таблицу); 2) зависимостью магнитной проницаемости μ от напряженности магнитного поля, вследствие чегозависимость В от Н для этих веществ является нелинейной; 3) наличием петли гистерезиса на кривой намагничивания; 4) существованием температуры, называемой точкой Кюри, выше которой ферромагнетик ведет себя как обычный парамагнетик. Из чистых металлов ферромагнетиками являются железо, никель, кобальт, а также некоторые редкоземельные металлы (например, гадолиний). К числу ферромагнетиков относятся сплавы и соединения этих металлов, а также сплавы и соединения марганца и хрома с неферромагнитными элементами (например, MnAlCu, CrTe и другие).Ферримагнетики(ферриты) – вещества, в которых магнитные моменты атомов кристаллической решетки образуют несколько магнитных подрешеток с магнитными моментами, направленными навстречудруг другу. Имея меньшую величину магнитной восприимчивости по сравнению с ферромагнетиками, в остальном ферримагнетики характеризуются теми же признаками, что и ферромагнетики. Типичными ферритами являются соединения оксидов железа с оксидами других металлов - шпинели (MnFe₂O₄), гранаты Gd₃Fe₅O₁₂), гексаферриты (PbFe₁₂O₁₉). Другую группу ферритов образуют двойные фториды типа RbNiF₃, а также соединения типа RFe₂ (R – редкоземельный металл).Антиферромагнетики– частный случай ферримагнетиков, в которых магнитные моменты подрешеток с противоположно направленными магнитными моментамиполностью компенсируют друг друга (скомпенсированный ферримагнетик). Существование антиферромагнетиков было предсказано Л.Д.Ландау в 1933г. В настоящее время известен широкий спектр веществ, обладающих антиферромагнитными свойствами: редкоземельные элементы (Er, Dy, Ho), оксиды и дифториды некоторых металлов (FeO, MnO, CoF₂, NiF₂), соли угольной и серной кислот (MnCO₃, NiSO₄) и другие. Сверхдиамагнетики (идеальные диамагнетики) – вещества, магнитная прони-цаемостьμ которых равна нулю. Благодаря этой особенности для сверхдиамагнетиков имеет местоэффект Мейсснера-Оксенфельда (Meissner W., 1882-1974; Ocksenfeld C.) – полное выталкивание магнитного поля из объема сверхдиамагнетика (магнитная индукцияВ=0). Сверхдиамагнетиками являются все вещества, находящиеся в сверхпроводящем состоянии -низкотемпературные сверхпроводники (металлы) и высокотемпературныесверхпроводники (керамики). Изнесверхпроводящих материалов, обладающих сверхдиамагнитными свойствами, известен пока только один пример – хлорид меди (CuCl), открытый в 1986г. (Русаков А.П., МИСиС). § 131. Магнитные моменты электронов и атомовРассматривая действие магнитного поля на проводники с током и на движущиеся заряды, мы не интересовались процесса­ми, происходящими в веществе. Свойства среды учитывались формально с помощью магнитной проницаемости . Для того что­бы разобраться в магнитных свойствах сред и их влиянии на магнитную индук­цию, необходимо рассмотреть действие магнитного поля на атомы и молекулы вещества.Опыт показывает, что все вещества, помещенные в магнитное поле, намагничи­ваются. Рассмотрим причину этого явле­ния с точки зрения строения атомов и мо­лекул, положив в основу гипотезу Ампера (см. § 109), согласно которой в любом теле существуют микроскопические токи,обусловленные движением электронов в атомах и молекулах.Для качественного объяснения маг­нитных явлений с достаточным приближе­нием можно считать, что электрон движет­ся в атоме по круговым орбитам. Элек­трон, движущийся по одной из таких орбит, эквивалентен круговому току, по­этому он обладает орбитальным магнит­ным моментом (см. (109.2)) p_m = ISn, мо­дуль которогоp_m=IS=evS, (131.1) где I = ev — сила тока, v — частота вра­щения электрона по орбите, S — площадь орбиты. Если электрон движется по часо­вой стрелке (рис. 187), то ток направлен против часовой стрелки и вектор р_m в со­ответствии с правилом правого винта направлен перпендикулярно плоскости орби­ты электрона.С другой стороны, движущийся по ор­бите электрон обладает механическим мо­ментом импульса L_e, модуль которого, со­гласно (19.1),

L_e=mvr=2mvS, (131.2)г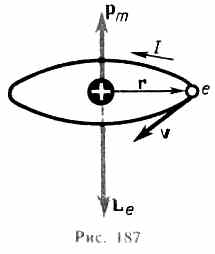де v=2vr, r²=S. Вектор L_e(его на­правление также подчиняется правилу правого винта), называется орбитальным механическим моментом электрона.

Из рис. 187 следует, что направления р_m и L_eпротивоположны, поэтому, учиты­вая выражения (131.1) и (131.2), получим

p_m=-(e/2m)L_e=gL_e, (131.3)где величинаg=-e/2m (131.4) называется гиромагнитным отношением орбитальных моментов (общепринято пи­сать со знаком « - », указывающим на то, что направления моментов противополож­ны). Это отношение, определяемое уни­версальными постоянными, одинаково для любой орбиты, хотя для разных орбит значения vи rразличны. Формула (131.4) выведена для круговой орбиты, но она справедлива и для эллиптических орбит. Экспериментальное определение гиро­магнитного отношения проведено в опытах Эйнштейна и де Гааза (1915), которые наблюдали поворот свободно подвешенно­го на тончайшей кварцевой нити железно­го стержня при его намагничении во внеш­нем магнитном поле (по обмотке соленои­да пропускался переменный ток с частотой, равной частоте крутильных колебаний стержня). При исследовании вынужден­ных крутильных колебаний стержня опре­делялось гиромагнитное отношение, кото­рое оказалось равным — (е/т). Таким об­разом, знак носителей, обусловливающих молекулярные токи, совпадал со знаком заряда электрона, а гиромагнитное отно­шение оказалось в два раза большим, чем введенная ранее величина g(см. (131.4)). Для объяснения этого результата, имев­шего большое значение для дальнейшего развития физики, было предположено, а впоследствии доказано, что кроме орби­тальных моментов (см. (131.1) и (131.2)) электрон обладает собственным механиче­ским моментом импульса L_es, называемым спином. Считалось, что спин обусловлен вращением электрона вокруг своей оси, что привело к целому ряду противоречий. В настоящее время установлено, что спин является неотъемлемым свойством элек­трона, подобно его заряду и массе. Спину электрона L_esсоответствует собственный (спиновый) магнитный момент p_ms, про­порциональный L_esи направленный в про­тивоположную сторону:p_ms=g_sL_es. (131.5) Величина g_sназывается гиромагнитным отношением спиновых моментов.Проекция собственного магнитного момента на направление вектора В может принимать только одно из следующих двух значений:где h=h/(2) (h— постоянная Планка), _в — магнетон Бора, являющийся едини­цей магнитного момента электрона.

В общем случае магнитный момент электрона складывается из орбитального и спинового магнитных моментов. Магнит­ный момент атома, следовательно, склады­вается из магнитных моментов входящих в его состав электронов и магнитного мо­мента ядра (обусловлен магнитными мо­ментами входящих в ядро протонов и ней­тронов). Однако магнитные моменты ядер в тысячи раз меньше магнитных моментов электронов, поэтому ими пренебрегают.Таким образом, общий магнитный момент атома (молекулы) р_а равен векторной сум­ме магнитных моментов (орбитальных и спиновых) входящих в атом (молекулу) электронов:p_а=р_m+р_ms. (131.6)Еще раз обратим внимание на то, что при рассмотрении магнитных моментов электронов и атомов мы пользовались классической теорией, не учитывая огра­ничений, накладываемых на движение электронов законами квантовой механики. Однако это не противоречит полученным результатам, так как для дальнейшего объяснения намагничивания веществ су­щественно лишь то, что атомы обладает магнитными моментами.