Закон Ампера. Закон БиоСавараЛапласа. Магнитная индукция прямого и кругового тока
 Скачать 2.54 Mb. Скачать 2.54 Mb.
|
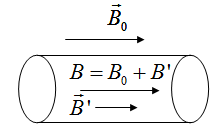
10-3 ÷ 10-5. А. Эйнштейн в 1905 г. показал, что явление фотоэффекта и его закономерности могут быть объяснены на основе предложенной им квантовой теории фотоэффекта. Согласно Эйнштейну, свет частотой v не только испускается, как это предполагал Планк (см. § 200), но и распространяется в пространстве и поглощается веществом отдельными порциями (квантами), энергия которых e0 = hv. Таким образом, распространение света нужно рассматривать не как непрерывный волновой процесс, а как поток локализованных в пространстве дискретных световых квантов, движущихся со скоростью с распространения света в вакууме. Кванты электромагнитного излучения получили название фотонов. По Эйнштейну, каждый квант поглощается только одним электроном. Поэтому число вырванных фотоэлектронов должно быть пропорционально интенсивности света (I закон фотоэффекта). Безынерционность фотоэффекта объясняется тем, что передача энергии при столкновении фотона с электроном происходит почти мгновенно. Энергия падающего фотона расходуется на совершение электроном работы выхода А из металла (см. § 104) и на сообщение вылетевшему фотоэлектрону кинетической энергии mv2max/2. По закону сохранения энергии, Уравнение (203.1) называется уравнением Эйнштейна для внешнего фотоэффекта. Уравнение Эйнштейна позволяет объяснить II и III законы фотоэффекта. Из (203.1) непосредственно следует, что максимальная кинетическая энергия фотоэлектрона линейно возрастает с увеличением частоты падающего излучения и не зависит от его интенсивности (числа фотонов), так как ни А, ни v от интенсивности света не зависят (II закон фотоэффекта). Так как с уменьшением частоты света кинетическая энергия фотоэлектронов уменьшается (для данного металла А=const), то при некоторой достаточно малой частоте v = v0 кинетическая энергия фотоэлектронов станет равной нулю и фотоэффект прекратится (III закон фотоэффекта). Согласно изложенному, из (203.1)получим, что Выражение (203.1) можно записать, используя (202.1) и (203.2), в виде Уравнение Эйнштейна было подтверждено опытами Милликена. В его приборе (1916 г.) поверхность исследуемого металла подвергалась очистке в вакууме. Исследовалась зависимость максимальной кинетической энергии фотоэлектронов (изменялось задерживающее напряжение U0(см. (202.1)) от частоты v и определялась постоянная Планка. В 1926 г. российские физики П. И. Лукирский (1894-1954) и С. С. Прилежаев для исследования фотоэффекта применили метод вакуумного сферического конденсатора. Анодом в их установке служили посеребренные стенки стеклянного сферического баллона, а катодом - шарик (R » 1,5 см) из исследуемого металла, помещенный в центр сферы. В остальном схема принципиально не отличается от описанной на рис. 289. Такая форма электродов позволила увеличить наклон вольт-амперных характеристик и тем самым более точно определять задерживающее напряжение U0 (а следовательно, и h). Значение h, полученное из данных опытов, согласуется со значениями, найденными другими методами (по излучению черного тела (§ 200) и по коротковолновой границе сплошного рентгеновского спектра (§ 299)). Все это является доказательством правильности уравнения Эйнштейна, а вместе с тем и его квантовой теории фотоэффекта. Если интенсивность света очень большая (лазерные пучки; см. § 233), то возможен многофотонный (нелинейный) фотоэффект, при котором электрон, испускаемый метал лом, может одновременно получить энергию не от одного, а отN фотонов (N=2¸7). Уравнение Эйнштейна для многофотонного фотоэффекта В опытах с фокусируемыми лазерными пучками плотность фотонов очень большая, поэтому электрон может поглотить не один, а несколько фотонов. При этом электрон может приобрести энергию, необходимую для выхода из вещества, даже под действием света с частотой, меньшей красной границы - порога однофотонного фотоэффекта. В результате красная граница смещается в сторону более длинных волн. Идея Эйнштейна о распространении света в виде потока отдельных фотонов и квантовом характере взаимодействия электромагнитного излучения с веществом подтверждена в 1922 г. опытами А. Ф. Иоффе и Н. И. Добронравова. В электрическом поле плоского конденсатора уравновешивалась заряженная пылинка из висмута. Нижняя обкладка конденсатора изготовлялась из тончайшей алюминиевой фольги, которая являлась одновременно анодом миниатюрной рентгеновской трубки. Анод бомбардировался ускоренными до 12 кВ фотоэлектронами, испускаемыми катодом под действием ультрафиолетового излучения. Освещенность катода подбиралась столь слабой, чтобы из него в 1 с вырывалось лишь 1000 фотоэлектронов, а следовательно, и число рентгеновских импульсов было 1000 в 1 с. Опыт показал, что в среднем через каждые 30 мин уравновешенная пылинка выходила из равновесия, т. е. рентгеновское излучение освобождало из нее фотоэлектрон. Если бы рентгеновское излучение распространялось в виде сферических волн, а не отдельных фотонов, то каждый рентгеновский импульс отдавал бы пылинке очень малую часть своей энергии, которая распределялась бы, в свою очередь, между огромным числом электронов, содержащихся в пылинке. Поэтому при таком механизме трудно вообразить, что один из электронов за такое короткое время, как 30 мин, может накопить энергию, достаточную для преодоления работы выхода из пылинки. Напротив, с точки зрения корпускулярной теории это возможно. Так, если рентгеновское излучение распространяется в виде потока дискретных фотонов, то электрон выбивается из пылинки только тогда, когда в нее попадает фотон. Элементарный расчет для выбранных условий дает, что в среднем в пылинку попадает один фотон из 1,8×106. Так как в 1 с вылетает 1000 фотонов, то в среднем в пылинку будет попадать один фотон в 30 мин, что согласуется с результатами опыта. Если свет представляет собой поток фотонов, то каждый фотон, попадая в регистрирующий прибор (глаз, фотоэлемент), должен вызывать то или иное действие независимо от других фотонов. Это же означает, что при регистрации слабых световых потоков должны наблюдаться флуктуации их интенсивности. Эти флуктуации слабых потоков видимого света действительно наблюдались С. И. Вавиловым. Наблюдения проводились визуально. Глаз, адаптированный к темноте, обладает довольно резким порогом зрительного ощущения, т. е. воспринимает свет, интенсивность которого не меньше некоторого порога. Для света с l = 525 нм порог зрительного ощущения соответствует у разных людей примерно 100-400 фотонам, падающим на сетчатку за 1 с. С. И. Вавилов наблюдал периодически повторяющиеся вспышки света одинаковой длительности. С уменьшением светового потока некоторые вспышки уже не воспринимались глазом, причем чем слабее был световой поток, тем больше было пропусков вспышек. Это объясняется флуктуациями интенсивности света, т. е. число фотонов оказывалось по случайным причинам меньше порогового значения. Таким образом, опыт Вавилова явился наглядным подтверждением квантовых свойств света. №5 Магнитные свойства вещества. Гипотеза Ампера. Напряженность магнитного поля. Намагниченность. Магнитная проницаемость и магнитная восприимчивость. Сила Лоренца- сила, действующая со стороны магнитного поля на движущуюся электрически заряженную частицу. Н Е 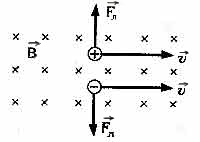 сли поставить левую руку так, чтобы перпендикулярная скорости составляющая вектора индукции входила в ладонь, а четыре пальца были бы расположены по направлению скорости движения положительного заряда (или против направления скорости отрицательного заряда), то отогнутый большой палец укажет направление силы Лоренца.Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы (т.е. не изменяет величину скорости заряда и его кинетическую энергию).Если заряженная частица движется параллельно силовым линиям магнитного поля, то Fл = 0 , и заряд в магнитном поле движется равномерно и прямолинейно.Если заряженная частица движется перпендикулярно силовым линиям магнитного поля, то сила Лоренца является центростремительной сли поставить левую руку так, чтобы перпендикулярная скорости составляющая вектора индукции входила в ладонь, а четыре пальца были бы расположены по направлению скорости движения положительного заряда (или против направления скорости отрицательного заряда), то отогнутый большой палец укажет направление силы Лоренца.Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы (т.е. не изменяет величину скорости заряда и его кинетическую энергию).Если заряженная частица движется параллельно силовым линиям магнитного поля, то Fл = 0 , и заряд в магнитном поле движется равномерно и прямолинейно.Если заряженная частица движется перпендикулярно силовым линиям магнитного поля, то сила Лоренца является центростремительнойВ этом случае частица движется по окружности. . тогда радиус окружности МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА М 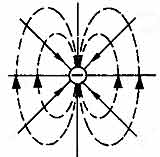 агнитные свойства вещества объясняются согласно гипотезе Амперациркулирующими внутри любого вещества замкнутыми токами: внутри атомов, вследствие движения электронов по орбитам, существуют элементарные электрические токи, которые создают элементарные магнитные поля. агнитные свойства вещества объясняются согласно гипотезе Амперациркулирующими внутри любого вещества замкнутыми токами: внутри атомов, вследствие движения электронов по орбитам, существуют элементарные электрические токи, которые создают элементарные магнитные поля.Поэтому: 1. если вещество не обладает магнитными свойствами - элементарные магнитные поля несориентированы ( из-за теплового движения); 2. если вещество обладает магнитными свойствами - элементарные магнитные поля одинаково направлены (сориентированы) и образуется собственное внутреннее магнитное поле вещества. Намагничевание вещества - появление собственного внутреннего магнитного поля. Все вещества, помещенные во внешнее магнитное поле, создают собственное внутреннее магнитное поле. По своим магнитным свойствам все вещества подразделяются на: парамагнетики [μ>1]- слабомагнитные вещества, внутреннее магнитное поле направлено также, как и внешнее магнитное поле, O2, Al, Pb и др.; диамагнетики [μ<1]– слабомагнитные вещества, внутреннее магнитное поле направлено противоположно внешнему магнитному полю, но слабовыраженно, гелий, аргон, Au , Zn, Cu, вода, стекло и др.; ферромагнетики[μ>>1] - сильномагнитные вещества, внутреннее магнитное поле в 100-1000 раз больше внешнего магнитного поля, небольшая группа кристаллич. тел: Fe, Ni, Co и сплавы. Ферромагнетики сохраняют сильную намагниченность и после удаления внешнего магнитного поля и называются постоянными магнитами. Сильное внутреннее магнитное поле ферромагнетиков объясняется не только обращением электронов по орбитам, но, в основном, вращением их вокруг собственной оси. Чтобы полностью размагнититьферромагнетик, надо поместить его во внешнее магнитное поле противоположно направленное. Существуют ферромагнетики, не проводящие электрический ток -ферриты.Точка КюриДля каждого ферромагнетика существует определенная температура - точка Кюри.1. Если t вещества < t Кюри, то вещество обладает ферромагнитными свойствами. 2. Если t вещества > t Кюри, то ферромагнитные свойства (намагниченность) исчезают, и вещество становится парамагнетиком.Поэтому постоянные магниты при нагревании теряют свои магнитные свойства.Магнитная проницаемость веществаЕсли проводник с током создает в вакууме магнитное поле с магнитной индукцией Во, то в другой среде магнитное поле, созданное этим же проводником с током будет иметь индукцию В. Т.е. значение магнитной индукции зависит от среды, в которой существует магнитное поле. Отношение магнитной индукции В поля в данной среде к магнитной индукции Во в вакууме, характеризует магнитные свойства данной среды и называется относительной магнитной проницаемостью вещества - µ. Применение ферромагнитов- постоянные магниты, изготовление магнитной ленты и пленки; - сердечники трансформаторов, генераторов, электродвигателей.Напряженность магнитного поля. Закон полного токаПонятие напряженности магнитного поля построено на формальной аналогии полей неподвижных зарядов и неподвижных намагниченных тел. Такая аналогия часто оказывается весьма полезной, т.к. позволяет перенести в теорию магнитного поля методы, разработанные дляэлектростатических полей.Напряженность магнитного поля первоначально была введена в форме закона Кулона через понятие магнитной массы, аналогичной электрическому заряду, как механическая сила взаимодействия двух точечных магнитных масс в однородной среде, которая пропорциональна произведению этих масс и обратно пропорциональна квадрату расстояния между ними,где m1 и m2 - взаимодействующие магнитные массы; r - расстояние между точками, в которых магнитные массы считаются сосредоточенными; k - коэффициент, зависящий от свойств среды и системы единиц измерения.Сила f направлена по прямой, соединяющей центры магнитных масс.Магнитные массы одного знака отталкиваются, а противоположного - притягиваются. Для количественной характеристики магнитного поля можно воспользоваться механической силой, действующей на положительный полюс пробного магнита, в той точке, где он расположен в пространстве. Напряженностью магнитного поляназывается отношение механической силы, действующей на положительный полюс пробного магнита, к величине его магнитной массы или механическая сила, действующая на положительный полюс пробного магнита единичной массы в данной точке поля. Напряженность изображается вектором H, имеющим направление вектора механической силы f. Если определить напряженность во всех точках магнитного поля, то можно построить линии, направление касательных к которым в каждой точке поля будет совпадать с направлением напряженности. Такие линии называются линиями напряженности или силовыми линиями. Можно также ввести понятие о силовой трубке магнитного поля аналогично тому, как это было сделано для магнитного потока.Силовые линии, в отличие от линий индукции магнитного поля, начинаются на положительных магнитных массах и заканчиваются на отрицательных, т.е. прерываются. Для изотропной среды существует связь между индукцией и напряженностью магнитного поляили Последнее соотношение можно использовать для определения магнитной проницаемости как отношения индукции к напряженности магнитного поля. При помещении в магнитное поле вещества в нем происходят процессы ориентации различных структур, обладающих дипольным магнитным моментом. Так электроны, перемещаясь по орбитам, образуют элементарные токи и соответствующие магнитные поля или магнитные диполи (рис. 1 а)). Кроме этого, электроны с 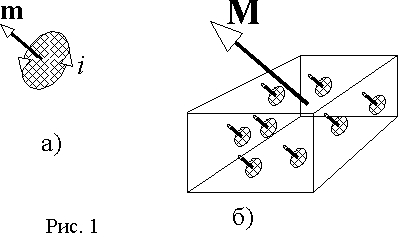 оздают магнитный момент за счет вращения вокруг собственной оси, называемый спиновым магнитным моментом. Магнитный диполь можно характеризовать вектором магнитного момента, численно равным произведению величины элементарного тока на площадь контура, ограниченного этим током в пространстве оздают магнитный момент за счет вращения вокруг собственной оси, называемый спиновым магнитным моментом. Магнитный диполь можно характеризовать вектором магнитного момента, численно равным произведению величины элементарного тока на площадь контура, ограниченного этим током в пространствеm = is,и направленным по нормали к площади контура. Геометрическая сумма всех магнитных моментов образует магнитный момент тела M = m, который обычно соотносят с объемом вещества V и называют намагниченностью или интенсивностью намагничивания Единицу измерения намагниченности можно определить из выражения (1) [J] = [M/V] = Ам2/м3 = А/м. Вектор намагниченности совпадает с направлением вектора напряженности и связан с ним линейной зависимостью. (2) Безразмерный коэффициент называется магнитной восприимчивостью вещества. Магнитная восприимчивость — физическая величина, характеризующая связь между магнитным моментом(намагниченностью) вещества и магнитным полем в этом веществе Для магнитного поля, существующего в некоторой среде, можно представить магнитную индукцию в виде суммы двух составляющих, индукции B0 , соответствующей вакууму, и дополнительной индукции Bн, создаваемой намагниченностью вещества У 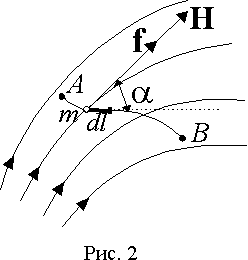 парамагнетиков >0 и >1. Например, у платины относительная магнитная проницаемость составляет 1,00036. Особую группу веществ, представляющих большой интерес с практической точки зрения, составляют ферромагнетики, у которых >>1 и составляет величину порядка 104 106. Определение напряженности магнитного поля через магнитные силы и массы не вполне адекватно физической картине явлений в магнитном поле, т.к., в отличие от электрического заряда, не существует массы или заряда магнитного. На практике удобнее пользоваться явлениями, связывающими между собой электрический ток и магнитное поле. Пусть некая точечная магнитная масса m перемещается по произвольному пути из точки A в точку B магнитного поля (рис. 2). Действующая на магнитную массу механическая сила f в любой точке поля направлена по касательной к силовой линии и равна f=mH , где H - напряженность поля. Работа по перемещению массы m по пути AB равна парамагнетиков >0 и >1. Например, у платины относительная магнитная проницаемость составляет 1,00036. Особую группу веществ, представляющих большой интерес с практической точки зрения, составляют ферромагнетики, у которых >>1 и составляет величину порядка 104 106. Определение напряженности магнитного поля через магнитные силы и массы не вполне адекватно физической картине явлений в магнитном поле, т.к., в отличие от электрического заряда, не существует массы или заряда магнитного. На практике удобнее пользоваться явлениями, связывающими между собой электрический ток и магнитное поле. Пусть некая точечная магнитная масса m перемещается по произвольному пути из точки A в точку B магнитного поля (рис. 2). Действующая на магнитную массу механическая сила f в любой точке поля направлена по касательной к силовой линии и равна f=mH , где H - напряженность поля. Работа по перемещению массы m по пути AB равна |

 χ > 0; µ > 1;
χ > 0; µ > 1;