Закон Ампера. Закон БиоСавараЛапласа. Магнитная индукция прямого и кругового тока
 Скачать 2.54 Mb. Скачать 2.54 Mb.
|
|
§ 132. Диа- и парамагнетизм В 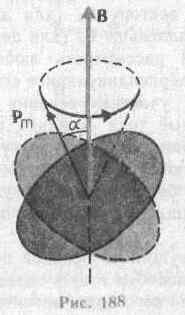 сякое вещество является магнетиком, т. е. оно способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Для понимания механизма этого явления необходимо рассмотреть действие магнитного поля на движущиеся в атоме электроны. сякое вещество является магнетиком, т. е. оно способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Для понимания механизма этого явления необходимо рассмотреть действие магнитного поля на движущиеся в атоме электроны.Ради простоты предположим, что электрон в атоме движется по круговой орбите. Если орбита электрона ориентирована относительно вектора В произвольным образом, составляя с ним угол а (рис. 188), то можно доказать, что она приходит в такое движение вокруг В, при котором вектор магнитного момента рm, сохраняя постоянным угол а, вращается вокруг направления В с некоторой угловой скоростью. Такое движение в механике называется прецессией. Прецессию вокруг вертикальной оси, проходящей через точку опоры, совершает, например, диск волчка при замедлении движения. Таким образом, электронные орбиты атома под действием внешнего магнитного поля совершают прецессионное движение, которое эквивалентно круговому току. Так как этот микроток индуцирован внешним магнитным полем, то, согласно правилу Ленца, у атома появляется составляющая магнитного поля, направленная противоположно внешнему полю. Наведенные составляющие магнитных полей атомов (молекул) складываются и образуют собственное магнитное поле вещества, ослабляющее внешнее магнитное поле. Этот эффект получил название диамагнитного эффекта, а вещества, намагничивающиеся во внешнем магнитном поле против направления поля, называются диамагнетиками.В отсутствие внешнего магнитного поля диамагнетик немагнитен, поскольку в данном случае магнитные моменты электронов взаимно компенсируются, и суммарный магнитный момент атома (он равен векторной сумме магнитных моментов (орбитальных и спиновых) составляющих атом электронов) равен нулю. К диамагнетикам относятся многие металлы (например, Bi, Ag, Au, Cu), большинство органических соединений, смолы, углерод и т. д.Так как диамагнитный эффект обусловлен действием внешнего магнитного поля на электроны атомов вещества, то диамагнетизм свойствен всем веществам. Однако наряду с диамагнитными веществами существуют и парамагнитные — вещества, намагничивающиеся во внешнем магнитном поле по направлению поля.У парамагнитных веществ при отсутствии внешнего магнитного поля магнитные моменты электронов не компенсируют друг друга, и атомы (молекулы) парамагнетиков всегда обладают магнитным моментом. Однако вследствие теплового движения молекул их магнитные моменты ориентированы беспорядочно, поэтому парамагнитные вещества магнитными свойствами не обладают. При внесении парамагнетика во внешнее магнитное поле устанавливается преимущественная ориентация магнитных моментов атомов по полю (полной ориентации препятствует тепловое движение атомов). Таким образом, парамагнетик намагничивается, создавая собственное магнитное поле, совпадающее по направлению с внешним полем и усиливающее его. Этот эффект называется парамагнитным. При ослаблении внешнего магнитного поля до нуля ориентация магнитных моментов вследствие теплового движения нарушается и парамагнетик размагничивается. К парамагнетикам относятся редкоземельные элементы, Pt, Al и т. д. Диамагнитный эффект наблюдается и в парамагнетиках, но он значительно слабее парамагнитного и поэтому остается незаметным.Из рассмотрения явления парамагнетизма следует, что его объяснение совпадает с объяснением ориентационной (дипольной) поляризации диэлектриков с полярными молекулами (см. §87), только электрический момент атомов в случае поляризации надо заменить магнитным моментом атомов в случае намагничения.Подводя итог качественному рассмотрению диа- и парамагнетизма, еще раз отметим, что атомы всех веществ являются носителями диамагнитных свойств. Если магнитный момент атомов велик, то парамагнитные свойства преобладают над диамагнитными и вещество является парамагнетиком; если магнитный момент атомов мал, то преобладают диамагнитные свойства и вещество является диамагнетиком. § 133. Намагниченность. Магнитное поле в веществеПодобно тому, как для количественного описания поляризации диэлектриков вводилась поляризованность (см. §88), для количественного описания намагничения магнетиков вводят векторную величину — намагниченность, определяемую магнитным моментом единицы объема магнетика:J=pm/V=pa/V,где pm=ра— магнитный момент маг-нетика, представляющий собой векторную сумму магнитных моментов отдельных молекул (см. (131.6)).Рассматривая характеристики магнитного поля (см. §109), мы вводили вектор магнитной индукции В, характеризующий результирующее магнитное поле, создаваемое всеми макро- и микротоками, и вектор напряженности Н, характеризующий магнитное поле макротоков. Следовательно, магнитное поле в веществе складывается их двух полей: внешнего поля, создаваемого током, и поля, создаваемого намагниченным веществом. Тогда вектор магнитной индукции результирующего магнитного поля в магнетике равен векторной сумме магнитных индукций внешнего поля В0 (поля, создаваемого намагничивающим током в вакууме) и поля микротоков В' (поля, создаваемого молекулярными токами):В = В0+В', (133.1) где В0=0Н (см. (109.3)). Для описания поля, создаваемого молекулярными токами, рассмотрим магнетик в виде кругового цилиндра сечения S и длины l, внесенного в однородное внешнее магнитное поле с индукцией Во. Возникающее в магнетике магнитное поле молекулярных токов будет направлено противоположно внешнему полю для диамагнетиков и совпадать с ним по направлению для парамагнетиков. Плоскости всех молекулярных токов расположатся перпендикулярно вектору Во, так как векторы их магнитных моментов рm антипараллельны вектору В0 (для диамагнетиков) и параллельны Во (для парамагнетиков). Если рассмотреть любое сечение цилиндра, перпендикулярное его оси, то во внутренних участках сечения магнетика молекулярные токи соседних атомов направлены навстречу друг другу и взаимно компенсируются (рис. 189). Нескомпенсированными будут лишь молекулярные токи, выходящие на боковую поверхность цилиндра.Ток, текущий по боковой поверхности цилиндра, подобен току в соленоиде и создает внутри него поле, магнитную индукцию В' которого можно вычислить, учитывая формулу (119.2) для N=1 (соленоид из одного витка):В 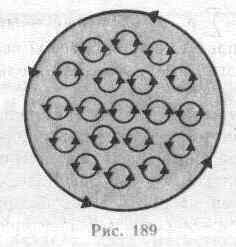 ' = 0I'/l(133.2)где I' — сила молекулярного тока, l — длина рассматриваемого цилиндра, а магнитная проницаемость принята равной единице.С другой стороны, I'/l — ток, приходящийся на единицу длины цилиндра, или его линейная плотность, поэтому магнитный момент этого тока p=I'lS/l=I'V/l, где V — объем магнетика. Если Р — магнитный момент магнетика объемом V, то P/V — намагниченность магнетика J. Таким образом,J= I'/l. (133.3)Сопоставляя (133.2) и (133.3), получим, что B'=0J, или в векторной форме B'=0J. Подставив выражения для В0 и В' в (133.1), получим В =0Н+0J, (133.4) или B/0=H+J. (133.5) Как показывает опыт, в несильных полях намагниченность прямо пропорциональна напряженности поля, вызывающего намагничение, т. е. J=H, (133.6)где — безразмерная величина, называемая магнитной восприимчивостью вещества. Для диамагнетиков отрицательна (поле молекулярных токов противоположно внешнему), для парамагнетиков — положительна (поле молекулярных токов совпадает с внешним). Используя формулу (133.6), выражение (133.4) можно записать в виде В = 0(1+)Н, (133.7) откуда Н=B/0(1+).Безразмерная величина =1+ (133.8) представляет собой магнитную проницаемость вещества. Подставив (133.8) в (133.7), придем к соотношению (109.3) В=0Н, которое ранее постулировалось.Так как абсолютное значение магнитной восприимчивости для диа- и парамагнетиков очень мало (порядка 10-4— 10-6), то для них незначительно отличается от единицы. Это просто понять, так как магнитное поле молекулярных токов значительно слабее намагничивающего поля. Т ' = 0I'/l(133.2)где I' — сила молекулярного тока, l — длина рассматриваемого цилиндра, а магнитная проницаемость принята равной единице.С другой стороны, I'/l — ток, приходящийся на единицу длины цилиндра, или его линейная плотность, поэтому магнитный момент этого тока p=I'lS/l=I'V/l, где V — объем магнетика. Если Р — магнитный момент магнетика объемом V, то P/V — намагниченность магнетика J. Таким образом,J= I'/l. (133.3)Сопоставляя (133.2) и (133.3), получим, что B'=0J, или в векторной форме B'=0J. Подставив выражения для В0 и В' в (133.1), получим В =0Н+0J, (133.4) или B/0=H+J. (133.5) Как показывает опыт, в несильных полях намагниченность прямо пропорциональна напряженности поля, вызывающего намагничение, т. е. J=H, (133.6)где — безразмерная величина, называемая магнитной восприимчивостью вещества. Для диамагнетиков отрицательна (поле молекулярных токов противоположно внешнему), для парамагнетиков — положительна (поле молекулярных токов совпадает с внешним). Используя формулу (133.6), выражение (133.4) можно записать в виде В = 0(1+)Н, (133.7) откуда Н=B/0(1+).Безразмерная величина =1+ (133.8) представляет собой магнитную проницаемость вещества. Подставив (133.8) в (133.7), придем к соотношению (109.3) В=0Н, которое ранее постулировалось.Так как абсолютное значение магнитной восприимчивости для диа- и парамагнетиков очень мало (порядка 10-4— 10-6), то для них незначительно отличается от единицы. Это просто понять, так как магнитное поле молекулярных токов значительно слабее намагничивающего поля. ТЗакон полного тока для магнитного поля в веществе (теорема о циркуляции вектора В) является обобщением закона (118.1): где I и I' — соответственно алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых произвольным замкнутым контуром L. Таким образом, циркуляция вектора магнитной индукции В по произвольному замкнутому контуру равна алгебраической сумме токов проводимости и молекулярных токов, охватываемых этим контуром, умноженной на магнитную постоянную. Вектор В, таким образом, характеризует результирующее поле, созданное как макроскопическими токами в проводниках (токами проводимости), так и микроскопическими токами в магнетиках, поэтому линии вектора магнитной индукции В не имеют источников и являются замкнутыми.Можно доказать, что циркуляция намагниченности J по произвольному замкнутому контуру L равна алгебраической сумме м Выражение (133.10) представляет собой теорему о циркуляции вектора Н. § 134. Условия на границе раздела двух магнетиков Р 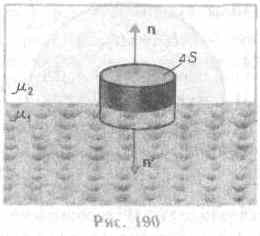 ассмотрим условия для векторов В и Н на границе раздела двух однородных магнетиков (магнитные проницаемости 1 и 2) при отсутствии на границе тока проводимости.Построим вблизи границы раздела магнетиков 1 и 2 прямой цилиндр ничтожно малой высоты, одно основание которого находится в первом магнетике, другое — во втором (рис. 190). Основания S настолько малы, что в пределах каждого из них вектор В одинаков. Согласно теореме Гаусса (120.3),B2nS-B1nS=0(нормали n и n' к основаниям цилиндра направлены противоположно). ПоэтомуВ1n=В2n. (134.1) Заменив, согласно В=(0Н, проекции вектора В проекциями вектора Н, умноженными на 0 получим Hn1/Hn2=2/1. (134.2) Вблизи границы раздела двух магнетиков 1 и 2 построим небольшой замкнутый прямоугольный контур ABCDAдлиной l, ориентировав его так, как показано на рис.191. Согласно теореме (133.10) о циркуляции вектора Н, ассмотрим условия для векторов В и Н на границе раздела двух однородных магнетиков (магнитные проницаемости 1 и 2) при отсутствии на границе тока проводимости.Построим вблизи границы раздела магнетиков 1 и 2 прямой цилиндр ничтожно малой высоты, одно основание которого находится в первом магнетике, другое — во втором (рис. 190). Основания S настолько малы, что в пределах каждого из них вектор В одинаков. Согласно теореме Гаусса (120.3),B2nS-B1nS=0(нормали n и n' к основаниям цилиндра направлены противоположно). ПоэтомуВ1n=В2n. (134.1) Заменив, согласно В=(0Н, проекции вектора В проекциями вектора Н, умноженными на 0 получим Hn1/Hn2=2/1. (134.2) Вблизи границы раздела двух магнетиков 1 и 2 построим небольшой замкнутый прямоугольный контур ABCDAдлиной l, ориентировав его так, как показано на рис.191. Согласно теореме (133.10) о циркуляции вектора Н, H2l-H1l=0 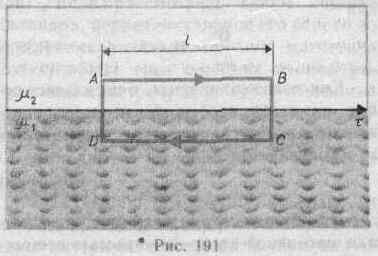 (знаки интегралов по ABи CDразные, так как пути интегрирования противоположны, а интегралы по участкам ВС и DAничтожно малы). Поэтому H1=H2. (134.3)Заменив, согласно B=0H, проекции вектора Н проекциями вектора В, деленными на 0, получим B1/B2=1/2. (134.4) Таким образом, при переходе через границу раздела двух магнетиков нормальная составляющая вектора В (Вn) и тангенциальная составляющая вектора Н (H) изменяются непрерывно (не претерпевают скачка), а тангенциальная составляющая вектора В (В)и нормальная составляющая вектора Н (Hn) претерпевают скачок. Из полученных условий (134.1) — (134.4) для составляющих векторов В и Н следует, что линии этих векторов испытывают излом (преломляются). Как и в случае диэлектриков (см. §90), можно найти закон преломления линий В (а значит, и линий Н): tg2/tg1=2/1. (предоставим это сделать по аналогии (см. §90) читателю). Из этой формулы следует, что, входя в магнетик с большей магнитной проницаемостью, линии В и Н удаляются от нормали. (знаки интегралов по ABи CDразные, так как пути интегрирования противоположны, а интегралы по участкам ВС и DAничтожно малы). Поэтому H1=H2. (134.3)Заменив, согласно B=0H, проекции вектора Н проекциями вектора В, деленными на 0, получим B1/B2=1/2. (134.4) Таким образом, при переходе через границу раздела двух магнетиков нормальная составляющая вектора В (Вn) и тангенциальная составляющая вектора Н (H) изменяются непрерывно (не претерпевают скачка), а тангенциальная составляющая вектора В (В)и нормальная составляющая вектора Н (Hn) претерпевают скачок. Из полученных условий (134.1) — (134.4) для составляющих векторов В и Н следует, что линии этих векторов испытывают излом (преломляются). Как и в случае диэлектриков (см. §90), можно найти закон преломления линий В (а значит, и линий Н): tg2/tg1=2/1. (предоставим это сделать по аналогии (см. §90) читателю). Из этой формулы следует, что, входя в магнетик с большей магнитной проницаемостью, линии В и Н удаляются от нормали. 135. Ферромагнетики и их свойства П 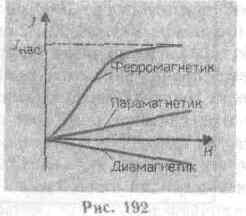 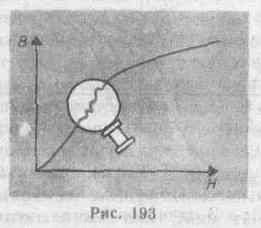 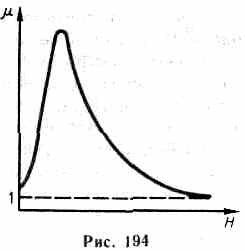 омимо рассмотренных двух классов веществ — диа- и парамагнетиков, называемых слабомагнитными веществами, существуют еще сильномагнитные вещества — ферромагнетики — вещества, обладающие спонтанной намагниченностью, т. е. они намагничены даже при отсутствии внешнего магнитного поля. К ферромагнетикам кроме основного их представителя — железа (от него и идет название «ферромагнетизм») — относятся, например, кобальт, никель, гадолиний, их сплавы и соединения. Ферромагнетики помимо способности сильно намагничиваться обладают еще и другими свойствами, существенно отличающими их от диа- и парамагнетиков. Если для слабомагнитных веществ зависимость J от Н линейна (см. (133.6) и рис. 192), то для ферромагнетиков эта зависимость, впервые изученная в 1878 г. методом баллистического гальванометра для железа русским физиком А. Г. Столетовым (1839—1896), является довольно сложной. По мере возрастания Н намагниченность J сначала растет быстро, затем медленнее и, наконец, достигается так называемое магнитное насыщение Jнас, уже не зависящее от напряженности поля. Подобный характер зависимости J от H можно объяснить тем, что по мере увеличения намагничивающего поля увеличивается степень ориентации молекулярных магнитных моментов по полю, однако этот процесс начнет замедляться, когда остается все меньше и меньше неориентированных моментов, и, наконец, когда все моменты будут ориентированы по полю, дальнейшее увеличение J прекращается и наступает магнитное насыщение. Магнитная индукция В=0(H+J) (см. (133.4)) в слабых полях растет быстро с ростом Н вследствие увеличения J, а в сильных полях, поскольку второе слагаемое постоянно (J=Jнас), В растет с увеличением Н по линейному закону (рис. 193). Существенная особенность ферромагнетиков — не только большие значения (например, для железа — 5000, для сплава супермаллоя — 800 000!), но и зависимость от Н (рис. 194). Вначале растет с увеличением Н, затем, достигая максимума, начинает уменьшаться, стремясь в случае сильных полей к 1 (=В/(0Н)=1+J/Н, поэтому при J=Jнас=const с ростом Н отношение J/H->0, а .->1). Характерная особенность ферромагнетиков состоит также в том, что для них зависимость J от H (а следовательно, и В от Н) определяется предысторией намагничения ферромагнетика. Это явление получило название магнитного гистерезиса. Если намагнитить ферромагнетик до насыщения (точка 1, рис. 195), а затем начать уменьшать напряженность Н намагничивающего поля, то, как показывает опыт, уменьшение J описывается кривой 1—2, лежащей выше кривой 1—0. При H=0 Jотличается от нуля, т. е. в ферромагнетике наблюдается остаточное намагничение Joc. С наличием остаточного намагничения связано существование постоянных магнитов. Намагничение обращается в нуль под действием поля НC, имеющего направление, противоположное полю, вызвавшему намагничение. омимо рассмотренных двух классов веществ — диа- и парамагнетиков, называемых слабомагнитными веществами, существуют еще сильномагнитные вещества — ферромагнетики — вещества, обладающие спонтанной намагниченностью, т. е. они намагничены даже при отсутствии внешнего магнитного поля. К ферромагнетикам кроме основного их представителя — железа (от него и идет название «ферромагнетизм») — относятся, например, кобальт, никель, гадолиний, их сплавы и соединения. Ферромагнетики помимо способности сильно намагничиваться обладают еще и другими свойствами, существенно отличающими их от диа- и парамагнетиков. Если для слабомагнитных веществ зависимость J от Н линейна (см. (133.6) и рис. 192), то для ферромагнетиков эта зависимость, впервые изученная в 1878 г. методом баллистического гальванометра для железа русским физиком А. Г. Столетовым (1839—1896), является довольно сложной. По мере возрастания Н намагниченность J сначала растет быстро, затем медленнее и, наконец, достигается так называемое магнитное насыщение Jнас, уже не зависящее от напряженности поля. Подобный характер зависимости J от H можно объяснить тем, что по мере увеличения намагничивающего поля увеличивается степень ориентации молекулярных магнитных моментов по полю, однако этот процесс начнет замедляться, когда остается все меньше и меньше неориентированных моментов, и, наконец, когда все моменты будут ориентированы по полю, дальнейшее увеличение J прекращается и наступает магнитное насыщение. Магнитная индукция В=0(H+J) (см. (133.4)) в слабых полях растет быстро с ростом Н вследствие увеличения J, а в сильных полях, поскольку второе слагаемое постоянно (J=Jнас), В растет с увеличением Н по линейному закону (рис. 193). Существенная особенность ферромагнетиков — не только большие значения (например, для железа — 5000, для сплава супермаллоя — 800 000!), но и зависимость от Н (рис. 194). Вначале растет с увеличением Н, затем, достигая максимума, начинает уменьшаться, стремясь в случае сильных полей к 1 (=В/(0Н)=1+J/Н, поэтому при J=Jнас=const с ростом Н отношение J/H->0, а .->1). Характерная особенность ферромагнетиков состоит также в том, что для них зависимость J от H (а следовательно, и В от Н) определяется предысторией намагничения ферромагнетика. Это явление получило название магнитного гистерезиса. Если намагнитить ферромагнетик до насыщения (точка 1, рис. 195), а затем начать уменьшать напряженность Н намагничивающего поля, то, как показывает опыт, уменьшение J описывается кривой 1—2, лежащей выше кривой 1—0. При H=0 Jотличается от нуля, т. е. в ферромагнетике наблюдается остаточное намагничение Joc. С наличием остаточного намагничения связано существование постоянных магнитов. Намагничение обращается в нуль под действием поля НC, имеющего направление, противоположное полю, вызвавшему намагничение. Н 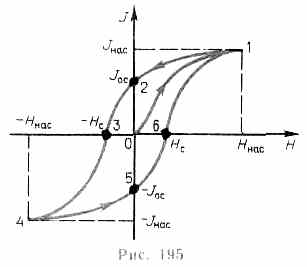 апряженность HC называется коэрцитивной силой. апряженность HC называется коэрцитивной силой.При дальнейшем увеличении противоположного поля ферромагнетик перемагничивается (кривая 3—4), и при H=-Hнас достигается насыщение (точка 4). Затем ферромагнетик можно опять размагнитить (кривая 4—5—6) и вновь перемагнитить до насыщения (кривая 6-1). Таким образом, при действии на ферромагнетик переменного магнитного поля намагниченность J изменяется в соответствии с кривой 1—2—3—4—5—6—1, которая называется петлей гистерезиса (от греч. «запаздывание»). Гистерезис приводит к тому, что намагничение ферромагнетика не является однозначной функцией H, т. е. одному и тому же значению H соответствует несколько значений J. Различные ферромагнетики дают разные гистерезисные петли. Ферромагнетики с малой (в пределах от нескольких тысячных до 1—2 А/см) коэрцитивной силой HC (с узкой петлей гистерезиса) называются мягкими, с большой (от нескольких десятков до нескольких тысяч ампер на сантиметр) коэрцитивной силой (с широкой петлей гистерезиса) — жесткими. Величины HC, Jос и max определяют применимость ферромагнетиков для тех или иных практических целей. Так, жесткие ферромагнетики (например, углеродистые и вольфрамовые стали) применяются для изготовления постоянных магнитов, а мягкие (например, мягкое железо, сплав железа с никелем) —для изготовления сердечников трансформаторов. Ферромагнетики обладают еще одной существенной особенностью: для каждого ферромагнетика имеется определенная температура, называемая точкой Кюри, при которой он теряет свои магнитные свойства. При нагревании образца выше точки Кюри ферромагнетик превращается в обычный парамагнетик. Переход вещества из ферромагнитного состояния в парамагнитное, происходящий в точке Кюри, не сопровождается поглощением или выделением теплоты, т. е. в точке Кюри происходит фазовый переход II рода (см. §75). Наконец, процесс намагничения ферромагнетиков сопровождается изменением его линейных размеров и объема. Это явление получило название магнитострикции. Величина и знак эффекта зависят от напряженности Я намагничивающего поля, от природы ферромагнетика и ориентации кристаллографических осей по отношению к полю. № 8. Модель атома Томсона. Опыты Резерфорда по рассеянию альфа-частиц. Ядерная модель атома. Постулаты Бора. Атом водорода по Бору. Сериальная формула. |
