Закон Ампера. Закон БиоСавараЛапласа. Магнитная индукция прямого и кругового тока

Название	Закон Ампера. Закон БиоСавараЛапласа. Магнитная индукция прямого и кругового тока
Анкор	shpora.doc
Дата	27.02.2017
Размер	2.54 Mb.
Формат файла
Имя файла	shpora.doc
Тип	Закон #3177
страница	2 из 12

1 2 3 4 5 6 7 8 9 ... 12

§ 198. ЗАКОН КИРХГОФА.Кирхгоф, опираясь на второй закон термодинамики и анализируя условия равновесного излучения в изолированной системе тел, установил количественную связь между спектральной плотностью энергетической светимости и спектральной поглощательной способностью тел. Отношение спектральной плотности энергетической светимости к спектральной поглощательной способности не зависит от природы тела; оно является для всех тел универсальной функцией частоты (длины волны) и температуры (закон Кирхгофа):

                                               (198.1)

Для черного тела А^ч_v_,_T ≡ 1, поэтому из закона Кирхгофа (см. (198.1)) вытекает, что R_v_,_Tдля черного тела равнаr_v_,_T. Таким образом, универсальная функция Кирхгофа r_v_,_T есть не что иное, как спектральная плотность энергетической светимости черного тела. Следовательно, согласно закону Кирхгофа, для всех тел отношение спектральной плотности энергетической светимости к спектральной плотности энергетической светимости к спектральной поглощательной способности равно спектральной плотности энергетической светимости черного тела при той же температуре и частоте.

Из закона Кирхгофа следует, что спектральная плотность энергетической светимости любого тела в любой области спектра всегда меньше спектральной плотности энергетической светимости черного тела (при тех же значениях Ти v), так как А_v_,_T < 1 и поэтому R_v_,_T < r_v_,_T.Кроме того, из (198.1) вытекает, что если тело при данной температуре T не поглощает электромагнитные волны в интервале частот от v до v+dv, то оно их в этом интервале частот при температуреT и не излучает, так как при А_v_,_T = 0 R_v_,_T = 0.

Используя закон Кирхгофа, выражение для энергетической светимости тела (197.2) можно записать в виде, где 2е выражение для сегоро тела.



                                     (198.2)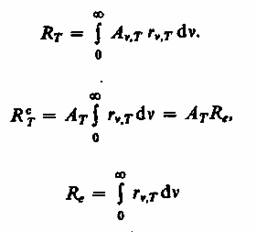

-

энергетическая светимость черного тела (зависит только от температуры).

Закон Кирхгофа описывает только тепловое излучение, являясь настолько характерным для него, что может служить надежным критерием для определения природы излучения. Излучение, которое закону Кирхгофа не подчиняется, не является тепловым.

§ 199. Законы Стефана-Больцмана и смещения Вина

Из закона Кирхгофа (см. (198.1)) следует, что спектральная плотность энергетической светимости черного тела является универсальной функцией, поэтому нахождение ее явной зависимости от частоты и температуры является важной задачей теории теплового излучения.

Австрийский физик И. Стефан (183S-1893), анализируя экспериментальные данные (1879), и Л. Больцман, применяя термодинамический метод (1884), решили эту задачу лишь частично, установив зависимость энергетической светимости Л, от температуры. Согласно закону Стефана - Больцмана,                                    (199.1)

т. е. энергетическая светимость черного тела пропорциональна четвертой степени его термодинамической температуры;s- постоянная Стефана - Больцмана: ее экспериментальное значение равно 5,67×10^-8 Вт/(м² ×К⁴).

Закон Стефана - Больцмана, определяя зависимость R_e от температуры, не дает ответа относительно спектрального состава излучения черного тела. Из экспериментальных кривых зависимости функции r_l_,_Tот длины волны l  при различных температурах (рис. 287) следует, что распределение энергии в спектре черного тела является неравномерным. Все кривые имеют явно выраженный максимум, который по мере повышения температуры смещается в сторону более коротких волн. Площадь, ограниченная кривой зависимости r_l_,_Tот l и осью абсцисс, пропорциональна энергетической светимости R_e, черного тела и, следовательно, по закону Стефана - Больцмана, четвертой степени температуры.
                                               Рис. 287

Немецкий физик В. Вин (1864-1928), опираясь на законы термо- и электродинамики, установил зависимость длины волны l_max, соответствующей максимуму функции r_l_,_T от температуры Т. Согласно закону смещения Вина,

(199.2)

т. е. длина волны l_max, соответствующая максимальному значению спектральной плотности энергетической светимостиr_l_,_Tчерного тела, обратно пропорциональна его термодинамической температуре, b - постоянная Вина; ее экспериментальное значение равно 2,9×10^-3 м×К. Выражение (199.2) потому называют законом смещения Вина, что оно показывает смещение положения максимума функции r_l_,_T по мере возрастания' температуры в область коротких длин волн. Закон Вина объясняет, почему при понижении температуры нагретых тел в их спектре все сильнее преобладает длинноволновое излучение (например, переход белого каления в красное при остывании металла).

§ 200. ФОРМУЛЫ РЭЛЕЯ - ДЖИНСА И ПЛАНКА Из рассмотрения законов Стефана - Больцмана и Вина следует, что термодинамический подход к решению задачи о нахождении универсальной функции Кирхгофа r_v_,_T не дал желаемых результатов. Следующая строгая попытка теоретического вывода зависимости r_v_,_T принадлежит английским ученым Д. Рэлею и Д. Джинсу (1877-1946), которые применили к тепловому излучению методы статистической физики, воспользовавшись классическим законом равномерного распределения энергии по степеням свободы.Формула Рэлея - Джннса для спектральной плотности энергетической светимости черного тела имеет вид

(200.1)

где áeñ = kT-средняя энергия осциллятора с собственной частотой v. Для осциллятора, совершающего колебания, средние значения кинетической и потенциальной энергий одинаковы (см. § 50), поэтому средняя энергия каждой колебательной степени свободы áeñ = kT.

Как показал опыт, выражение (200.1) согласуется с экспериментальными данными только в области достаточно малых частот и больших температур. В области больших частот формула Рэлея - Джинса резко расходится с экспериментом, а также с законом смещения Вина (рис. 288). Кроме того, оказалось, что попытка получить закон Стефана - Больцмана (см. (199.1)) из формулы Рэлея - Джинса приводит к абсурду. Действительно, вычисленная с использованием (200.1) энергетическая светимость черного тела (см. (198.3))

в то время как по закону Стефана - Больцмана R_eпропорциональна четвертой степени температуры. Этотрезультат получил название «ультрафиолетовой катастрофы». Таким образом, в рамках классической физики не удалось объяснить законы распределения энергии в спектре черного тела.

В области больших частот хорошее согласие с опытом дает формула Вина (закон излучения Вина), полученная им из общих теоретических соображений: r_v_1,_T= Cv³Ae^-^Av^/^Tгде r_v_1,_T - спектральная плотность энергетической светимости черного тела, С и А - постоянные величины. В современных обозначениях с использованием постоянной Планка, которая в то время еще не была известна, закон излучения Вина может быть записан в виде

Правильное, согласующееся с опытными данными выражение для спектральной плотности энергетической светимости черного тела было найдено в 1900 г. немецким физиком М. Планком. Для этого ему пришлось отказаться от установившегося положения классической физики, согласно которому энергия любой системы может изменятьсянепрерывно, т. е. может принимать любые сколь угодно близкие значения. Согласно выдвинутой Планком квантовой гипотезе, атомные осцилляторы излучают энергию не непрерывно, а определенными порциями - квантами, причем энергия кванта пропорциональна частоте колебания (см. (170.3)):

(200.2)

где h=6,625×10^-34 Дж×с - постоянная Планка. Так как излучение испускается порциями, то энергия осциллятора е может принимать лишь определенные дискретные значения, кратные целому числу элементарных порций энергии e₀:

В данном случае среднюю энергию áeñ осциллятора нельзя принимать равной kT. В приближении, что распределение осцилляторов по возможным дискретным состояниям подчиняется распределению Больцмана (§ 45), средняя энергия осциллятора

а спектральная плотность энергетической светимости черного тела

Таким образом, Планк вывел для универсальной функции Кирхгофа формулу

(200.3)

которая блестяще согласуется с экспериментальными данными по распределению энергии в спектрах излучения черного тела во всем интервале частот и температур. Теоретический вывод этой формулы М. Планк изложил 14 декабря 1900 г. на заседании Немецкого физического общества. Этот день стал датой рождения квантовой физики.

В области малых частот, т. е. при hv << kT(энергия кванта очень мала по сравнению с энергией теплового движения kT), формула Планка (200.3) совпадает с формулой Рэлея - Джинса (200.1). Для доказательства этого разложим экспоненциальную функцию в ряд, ограничившись для рассматриваемого случая двумя первыми членами:

Подставляя последнее выражение в формулу Планка (200.3), найдем, что

т. е. получили формулу Рэлея - Джинса (200.1).

Из формулы Планка можно получить закон Стефана - Больцмана. Согласно (198.3) и (200.3),

Введем безразмерную переменную x = hv/(kT); dx = hdv/(kT);dv = kTdx/h. Формула для R_e, преобразуется к виду

(200.4)

. Таким образом, действительно формула Планка позволяет получить закон Стефана - Больцмана (ср. формулы (199.1) и (200.4)). Кроме того, подстановка числовых значений k, си h дает для постоянной Стефана - Больцмана значение, хорошо согласующееся с экспериментальными данными. Закон смещения Вина получим с помощью формул (197.1) и (200.3):

Откуда

Значение l_max, при котором функция достигает максимума, найдем, приравняв нулю эту производную. Тогда, введя x = hc/(kTl_max), получим уравнение

Решение этого трансцендентного уравнения методом последовательных приближений дает х=4,965. Следовательно, hc/(kTl_max) = 4,965, откуда

т. е. получили закон смещения Вина (см. (199.2)).

Из формулы Планка, зная универсальные постоянные h, k и с, можно вычислить постоянные Стефана - Больцманаа и Вина b. С другой стороны, зная экспериментальные значения а и b, можно вычислить значения А и k (именно так и было впервые найдено числовое значение постоянной Планка).

Таким образом, формула Планка не только хорошо согласуется с экспериментальными данными, но и содержит в себе частные законы теплового излучения, а также позволяет вычислить постоянные в законах теплового излучения. Следовательно, формула Планка является полным решением основной задачи теплового излучения, поставленной Кирхгофом. Ее решение стало возможным лишь благодаря революционной квантовой гипотезе Планка.

№3Магнитный момент кругового тока. Теорема циркуляции. Сила Лоренца. Движение заряженных частиц в однородном магнитном поле.Сила Лоренца. Движение заряженной частицы в однородном постоянном магнитном поле Основные формулы   Сила, действующая на электрический заряд q, движущийся со скоростью v в магнитном поле ,          (18) где  – вектор магнитной индукции поля. Модуль силы, действующей на заряженную частицу, движущуюся в магнитном поле ,    (19)

где q – модуль заряда частицы; v – модуль вектора скорости; B – модуль вектора индукции магнитного поля, α – угол между векторами v и B.

Направление силы  определяется по правилу левой руки:если ладонь левой руки расположить так, чтобы в нее входил вектор магнитной индукции B, а четыре вытянутых пальца направить вдоль скорости движения положительного заряда (против направления движения отрицательного заряда), то отогнутый на 90° большой палец покажет направление силы, действующей на заряд.

  Если заряд движется в области, где существуют одновременно электрическое и магнитное поля, то на него действует полная сила ,(20) формула (20) называется формулой Лоренца.Методические рекомендации

1. Полная электромагнитная сила (сила Лоренца), действующая на заряд, определяется формулой (20). Данная формула справедлива как для постоянных, так и для переменных электрических и магнитных полей.

Эту силу разделяют на электрическую и магнитную составляющие. Если заряженная частица находится только в магнитном поле, то силу, определяемую выражением (18), обычно и называют силой Лоренца.

Важная особенность силы Лоренца – она всегда перпендикулярна вектору скорости заряда и поэтому не совершает над зарядом работы. Следовательно, в постоянном магнитном поле энергия движущейся заряженной частицы всегда постоянна.

Разделение полной электромагнитной силы на электрическую и магнитную зависит от выбора системы отсчета, так как магнитная составляющая силы Лоренца меняется при переходе от одной системы отсчета к другой, а значит, меняется и электрическая составляющая.

2. Под действием силы Лоренца заряженные частицы движутся в магнитном поле по криволинейным траекториям. Характер движения частицы в магнитном поле зависит от угла между первоначальным направлением скорости движения частицы и направлением линий индукции магнитного поля.

     Если скорость частицы перпендикулярна линиям магнитной индуции, то частица движется по круговой траектории (рис. 23).

Радиус окружности траектории

;

Рис. 23

период вращения частицы по окружности:,

где  m– масса частицы; v– модуль скорости частицы;B – модуль вектора индукции магнитного поля;  q– модуль электрического заряда.

  Если заряженная частица движется вдоль линий магнитной индукции, сила Лоренца на нее не действует и характер ее движения не меняется.

   Если угол  α между первоначальным направлением скорости частицы и линиями магнитной индукции не равен ни 0°, ни 90°, ни 180°, траектория движения частицы представляет собой винтовую линию, накручивающуюся на линии магнитной индукции (рис. 24).

Рис. 24

– тангенциальная составляющая скорости ; ; – нормальная составляющая скорости; ; – шаг винтовой линии; .

3. При движении заряженной частицы в области пространства, занятой одновременно и электрическим и магнитным полями характер ее движения зависит от направления этих полей и величины сил, действующих с их стороны, а также от скорости частицы.

► Векторы E иB  взаимно-перпендикулярны и скорость v положительно заряженной частицы перпендикулярна силовым линиям этих полей. В этом случае на частицу действуют две силы: электрическая  и магнитная , которые могут быть как сонаправлены, так и противоположно направлены. Если силы противоположно направлены и равны по модулю (), то частица будет двигаться равномерно и прямолинейно, согласно первому закону Ньютона.

В случае если силы не уравновешивают друг друга, то движение частицы будет сложным: она будет двигаться с ускорением вдоль линии напряженности электрического поля и совершать вращательное движение вокруг линии индукции магнитного поля.

Если силы, действующие на движущуюся заряженную частицу сонаправлены, то движение частицы также будет представлять суперпозицию двух движений: прямолинейного с ускорением вдоль линий вектора  и вращательного вокруг линий вектора .

Частица влетает в область пространства параллельно векторам E и B. В этом случае на нее действует только электрическая сила  (сила Лоренца , так как  и ). Под действием этой силы  частица движется прямолинейно с ускорением .

Закон Био–Савара. Теорема о циркуляции *)
Магнитное поле постоянных токов различной конфигурации изучалось экспериментально французскими учеными Ж. Био и Ф. Саваром (1820 г.). Они пришли к выводу, что индукция магнитного поля токов, текущих по проводнику, определяется совместным действием всех отдельных участков проводника. Магнитное поле подчиняется принципу суперпозиции:

Если магнитное поле создается несколькими проводниками с током, то индукция результирующего поля есть векторная сумма индукций полей, создаваемых каждым проводником в отдельности.

И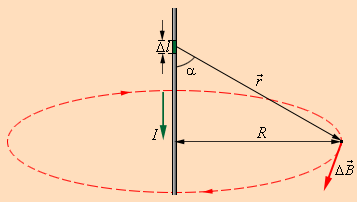

ндукцию В проводника с током можно представить как векторную сумму элементарных индукций ∆В создаваемых отдельными участками проводника. На опыте невозможно осуществить отдельный участок проводника с током, так как постоянные токи всегда замкнуты. Можно измерить только суммарную индукцию магнитного поля, создаваемого всеми элементами тока. Закон Био–Савара определяет вклад ∆В в магнитную индукцию В результирующего магнитного поля, создаваемый малым участком Δl проводника с током I. Здесь r – расстояние от данного участка Δl до точки наблюдения, α – угол между направлением на точку наблюдения и направлением тока на данном участке, μ₀ – магнитная постоянная. Направление вектора ∆В определяется правилом буравчика: оно совпадает с направлением вращения рукоятки буравчика при его поступательном перемещении вдоль тока. Рис. 4.17.1 иллюстрирует закон Био–Савара на примере магнитного поля прямолинейного проводника с током. Если просуммировать (проинтегрировать) вклады в магнитное поле всех отдельных участков прямолинейного проводника с током, то получится формула для магнитной индукции поля прямого тока: которая уже приводилась в § 1.16

Закон Био–Савара позволяет рассчитывать магнитные поля токов различных конфигураций. Нетрудно, например, выполнить расчет магнитного поля в центре кругового витка с током. Этот расчет приводит к формуле

где R – радиус кругового проводника. Для определения направления вектора В также можно использовать правило буравчика, только теперь его рукоятку нужно вращать в направлении кругового тока, а поступательное перемещение буравчика укажет направление вектора магнитной индукции.

Расчеты магнитного поля токов часто упрощаются при учете симметрии в конфигурации токов, создающих поле. В этом случае расчеты можно выполнять с помощью теоремы о циркуляции вектора магнитной индукции, которая в теории магнитного поля токов играет ту же роль, что и теорема Гаусса в электростатике.

Поясним понятие циркуляции вектора B . Пусть в пространстве, где создано магнитное поле, выбран некоторый условный замкнутый контур (не обязательно плоский) и указано положительное направление обхода контура. На каждом отдельном малом участке Δl этого контура можно определить касательную составляющую B_l вектора B в данном месте, то есть определить проекцию вектора B на направление касательной к данному участку контура (рис. 4.17.2).

Рисунок 4.17.2.

Замкнутый контур (L) с заданным направлением обхода. Изображены токи I₁, I₂ и I₃, создающие магнитное поле. Циркуляцией вектора B называют сумму произведений B_l Δl, взятую по всему контуру L:

Некоторые токи, создающие магнитное поле, могут пронизывать выбранный контур L в то время, как другие токи могут находиться в стороне от контура.

Теорема о циркуляции утверждает, что циркуляция вектора B магнитного поля постоянных токов по любому контуру L всегда равна произведению магнитной постоянной μ₀ на сумму всех токов, пронизывающих контур:

В качестве примера на рис. 4.17.2 изображены несколько проводников с токами, создающими магнитное поле. Токи I₂ и I₃ пронизывают контур L в противоположных направлениях, им должны быть приписаны разные знаки – положительными считаются токи, которые связаны с выбранным направлением обхода контура правилом правого винта (буравчика). Следовательно, I₃ > 0, а I₂ < 0. Ток I₁ не пронизывает контур L.Теорема о циркуляции в данном примере выражается соотношением:

Теорема о циркуляции в общем виде следует из закона Био–Савара и принципа суперпозиции.

Простейшим примером применения теоремы о циркуляции является определение магнитной индукции поля прямолинейного проводника с током. Учитывая симметрию в данной задаче, контур L целесообразно выбрать в виде окружности некоторого радиуса R, лежащей в перпендикулярной проводнику плоскости. Центр окружности находится в некоторой точке проводника. В силу симметрии вектор В направлен по касательной (B_l=B ), а его модуль одинаков во всех точках окружности. Применение теоремы о циркуляции приводит к соотношению: откуда следует формула для модуля магнитной индукции поля прямолинейного проводника с током, приведенная ранее. Этот пример показывает, что теорема о циркуляции вектора магнитной индукции B может быть использована для расчета магнитных полей, создаваемых симметричным распределением токов, когда из соображений симметрии можно «угадать» общую структуру поля.

Имеется немало практически важных примеров расчета магнитных полей с помощью теоремы о циркуляции. Одним из таких примеров является задача вычисления поля тороидальной катушки (рис. 4.17.3).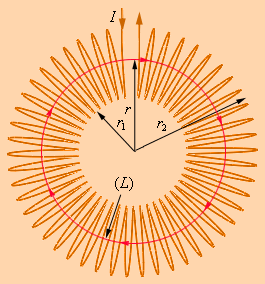

Рисунок 4.17.3.

Применение теоремы о циркуляции к тороидальной катушке.Предполагается, что катушка плотно, то есть виток к витку, намотана на немагнитный тороидальный сердечник. В такой катушке линии магнитной индукции замыкаются внутри катушки и представляют собой концентрические окружности. Они направлены так, что глядя вдоль них, мы увидели бы ток в витках, циркулирующим по часовой стрелке. Одна из линий индукции некоторого радиуса r₁ ≤ r < r₂ изображена на рис. 4.17.3. Применим теорему о циркуляции к контуру L в виде окружности, совпадающей с изображенной на рис. 4.17.3 линией индукции магнитного поля. Из соображений симметрии ясно, что модуль вектора B одинаков вдоль всей этой линии. По теореме о циркуляции можно записать: B ∙ 2πr = μ₀IN, где N – полное число витков, а I – ток, текущий по виткам катушки. Следовательно,

Таким образом, модуль вектора магнитной индукции в тороидальной катушке зависит от радиуса r. Если сердечник катушки тонкий, то есть r₂ – r₁ << r, то магнитное поле внутри катушки практически однородно. Величина n = N / 2πr представляет собой число витков на единицу длины катушки. В этом случае B = μ₀In.

В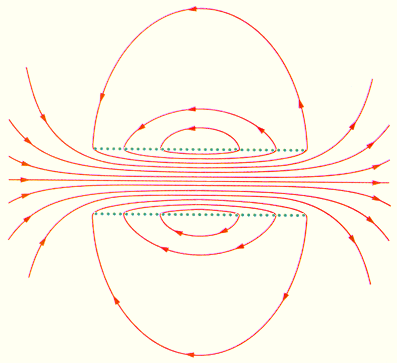

это выражение не входит радиус тора, поэтому оно справедливо и в предельном случае r → ∞. Но в пределе каждую часть тороидальной катушки можно рассматривать как длинную прямолинейную катушку. Такие катушки называют соленоидами. Вдали от торцов соленоида модуль магнитной индукции выражается тем же соотношением, что и в случае тороидальной катушки.На рис. 4.17.4 изображено магнитное поле катушки конечной длины. Следует обратить внимание на то, что в центральной части катушки магнитное поле практически однородно и значительно сильнее, чем вне катушки. На это указывает густота линий магнитной индукции. В предельном случае бесконечно длинного соленоида однородное магнитное поле целиком сосредоточено внутри соленоида. Рисунок 4.17.4.

Магнитное поле катушки конечной длины. В центре соленоида магнитное поле практически однородно и значительно превышает по модулю поле вне катушки.

В случае бесконечно длинного соленоида выражение для модуля магнитной индукции можно получить непосредственно с помощью теоремы о циркуляции, применив ее к прямоугольному контуру, показанному на рис. 4.17.5. Р

исунок 4.17.5. Применение теоремы о циркуляции к расчету магнитного поля бесконечно длинного соленоидаВектор магнитной индукции имеет отличную от нуля проекцию на направление обхода контура abcd только на стороне ab. Следовательно, циркуляция вектора B по контуру равна Bl, где l – длина стороны ab. Число витков соленоида, пронизывающих контур abcd, равно n · l, где n – число витков на единицу длины соленоида, а полный ток, пронизывающий контур, равен Inl. Согласно теореме о циркуляции, Bl = μ₀Inl откуда B = μ₀In

Это выражение совпадает с полученной ранее формулой для магнитного поля тонкой тороидальной катушки.В предыдущем параграфе было выяснено, что действие магнитного поля на плоский контур с током определяется магнитным моментом контура pm, равным произведению силы тока I в контуре на площадь контура S:pm=IS (см. формулу (118.1)).
Единицей магнитного момента является ампер-метр в квадрате (А•м2). Чтобы дать представление об этой единице, укажем, что при силе тока 1 А магнитным моментом, равным 1 А•м2, обладает круговой контур радиуса 0,564 м (p•0,5642=1) либо квадратный контур со стороной квадрата, равной 1 м. При силе тока 10 А магнитным моментом 1 А•м2 обладает круговой контур радиуса 0,178 м (p•0,1782=0,1) и т. д.
Электрон, движущийся с большой скоростью по круговой орбите, эквивалентен круговому току, сила которого равна произведению заряда электрона е на частоту n вращения электрона по орбите: I=en. Если радиус орбиты равен r, а скорость электрона — v, то n=vl2pr и, следовательно, I=ev/2pr. Магнитный момент, соответствующий этому току,

Магнитный момент является векторной величиной, направленной по нормали к контуру. Из двух возможных направлений нормали выбирается то, которое связано с направлением тока в контуре правилом правого винта [{рис. 211). Вращение винта с правой нарезкой в направлении, совпадающем с направлением тока в контуре, вызывает продольное перемещение винта в направлении n. Выбранная таким образом нормаль называется положительной. Направление вектора pm принимается совпадающим с направлением положительной нормали n.
Теперь мы можем уточнить определение направления магнитной индукции В. За направление магнитной индукции В принимается направление, в котором устанавливается под действием поля положительная нормаль к контуру с током, т. е. направление, в котором устанавливается вектор pm.
Единица магнитной индукции в СИ называется тесла (Тл) в честь сербского ученого Николы Теслы (1856—1943). Один тесла равен магнитной индукции однородного магнитного поля, в котором на плоский контур с током, имеющий магнитный момент один ампер-метр в квадрате, действует максимальный вращающий момент, равный одному ньютон-метру.
Из формулы (118.2) следует, что

№4 Гипотеза Планка. Квантовое объяснение законов теплового излучения. Корпускулярно-волновой дуализм света.Внешний фотоэффект. Законы фотоэффекта. Уравнение Эйнштейна для фотоэффекта. Определение постоянной Планка.

200. ФОРМУЛЫ РЭЛЕЯ - ДЖИНСА И ПЛАНКА

Из рассмотрения законов Стефана - Больцмана и Вина следует, что термодинамический подход к решению задачи о нахождении универсальной функции Кирхгофа r_v_,_T не дал желаемых результатов. Следующая строгая попытка теоретического вывода зависимости r_v_,_T принадлежит английским ученым Д. Рэлею и Д. Джинсу (1877-1946), которые применили к тепловому излучению методы статистической физики, воспользовавшись классическим законом равномерного распределения энергии по степеням свободы.

Формула Рэлея - Джннса для спектральной плотности энергетической светимости черного тела имеет вид

(200.1) где = kT-средняя энергия осциллятора с собственной частотой v. Для осциллятора, совершающего колебания, средние значения кинетической и потенциальной энергий одинаковы (см. § 50), поэтому средняя энергия каждой колебательной степени свободы = kT.

Как показал опыт, выражение (200.1) согласуется с экспериментальными данными только в области достаточно малых частот и больших температур. В области больших частот формула Рэлея - Джинса резко расходится с экспериментом, а также с законом смещения Вина (рис. 288). Кроме того, оказалось, что попытка получить закон Стефана - Больцмана (см. (199.1)) из формулы Рэлея - Джинса приводит к абсурду. Действительно, вычисленная с использованием (200.1) энергетическая светимость черного тела (см. (198.3))

в то время как по закону Стефана - Больцмана R_eпропорциональна четвертой степени температуры. Этотрезультат получил название «ультрафиолетовой катастрофы». Таким образом, в рамках классической физики не удалось объяснить законы распределения энергии в спектре черного тела.

В области больших частот хорошее согласие с опытом дает формула Вина (закон излучения Вина), полученная им из общих теоретических соображений:r_v_1,_T= Cv³Ae^-^Av^/^T

где r_v_1,_T - спектральная плотность энергетической светимости черного тела, С и А - постоянные величины. В современных обозначениях с использованием постоянной Планка, которая в то время еще не была известна, закон излучения Вина может быть записан в виде

(200.2)

где h=6,625×10^-34 Дж×с - постоянная Планка. Так как излучение испускается порциями, то энергия осциллятора е может принимать лишь определенные дискретные значения, кратные целому числу элементарных порций энергии eВ данном случае среднюю энергию осциллятора нельзя принимать равной kT. В приближении, что распределение осцилляторов по возможным дискретным состояниям подчиняется распределению Больцмана (§ 45), средняя энергия осциллятора

а спектральная плотность энергетической светимости черного тела

Таким образом, Планк вывел для универсальной функции Кирхгофа формулу

Подставляя последнее выражение в формулу Планка (200.3), найдем, что

Введем безразмерную переменную x = hv/(kT); dx = hdv/(kT);dv = kTdx/h. Формула для R_e, преобразуется к виду

(200.4)

Откуда

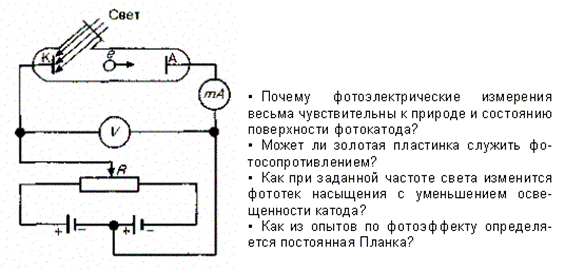Рис. 289

Два электрода (катод К из исследуемого металла и анод А - в схеме Столетова применялась металлическая сетка) в вакуумной трубке подключены к бата рее так, что с помощью потенциометра R можно изменять не только значение, но и знак подаваемого на них напряжения. Ток, возникающий при освещении катода монохроматическим светом (через кварцевое окошко), измеряется включенным в цепь миллиамперметром. Облучая катод светом различных длин волн, Столетов установил следующие закономерности, не утратившие своего значения до нашего времени: 1) наиболее эффективное действие оказывает ультрафиолетовое излучение; 2) под действием света вещество теряет только отрицательные заряды; 3) сила тока, возникающего под действием света, прямо пропорциональна его интенсивности.

Дж. Дж. Томсон в 1898 г. измерил удельный заряд испускаемых под действием света частиц, (по отклонению в электрическом и магнитном полях). Эти измерения показали, что под действием света вырываются электроны.

Внутренний фотоэффект - это вызванные электромагнитным излучением переходы электронов внутри полупроводника или диэлектрика из связанных состояний в свободные без вылета наружу. В результате концентрация носителей тока внутри, тела увеличивается, что приводит к возникновению фотопроводимости (повышению электропроводности полупроводника или диэлектрика при его освещении) или к возникновению э.д.с.

Вентильный фотоэффект, являющийся разновидностью внутреннего фотоэффекта, - возникновение э.д.с. (фото-э.д.с.) при освещении контакта двух разных полупроводников или полупроводника и металла (при отсутствии внешнего электрического поля). Вентильный фотоэффект открывает, таким образом, пути для прямого преобразования солнечной энергии в электрическую.

Н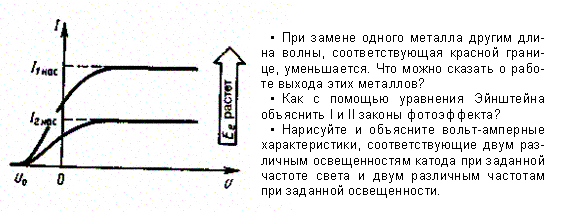

а рис. 289 приведена экспериментальная установка для исследования вольт-ампер ной характеристики фотоэффекта - зависимости фототока /, образуемого потоком электронов, испускаемых катодом под действием света, от напряжения U между электродами. Такая зависимость, соответствующая двум различным освещенностям Е, катода (частота света в обоих случаях одинакова), приведена на рис. 290. По мере увеличения U фототок постепенно возрастает, т. е. все большее число фотоэлектронов достигает анода. Пологий характер кривых показывает, что электроны вылетают из катода с различными скоростями. Максимальное значение тока I_нас - фототок насыщения - определяется таким значением U, при котором все электроны, испускаемые катодом, достигают анода:

где n - число электронов, испускаемых катодом в 1 с.

Из вольт-амперной характеристики следует, что при U = 0 фототок не исчезает. Следовательно, электроны, выбитые светом из катода, обладают некоторой начальной скоростью v, а значит, и отличной от нуля кинетической энергией и могут достигнуть анода без внешнего поля. Для того чтобы фототек стал равным нулю, необходимо приложить задерживающее напряжение U₀.При U = U₀ни один из электронов, даже обладающий при вылете из катода максимальной скоростью v_max, не может преодолеть задерживающего поля и достигнуть анода. Следовательно,

                        (202.1)

т. е., измерив задерживающее напряжение U₀, можно определить максимальные значения скорости и кинетической энергии фотоэлектронов.

При изучении вольт-амперных характеристик разнообразных материалов (важна чистота поверхности, поэтому измерения проводятся в вакууме и на свежих поверхностях) при различных частотах падающего на катод излучения и различных энергетических освещенностях катода и обобщения полученных данных были установлены следующие три закона внешнего фотоэффекта.

I. Закон Столетова: при фиксированной частоте падающего света число фотоэлектронов, вырываемых из катода в единицу времени, пропорционально интенсивности света (сила фототока насыщения пропорциональна энергетической освещенности Е_екатода).

II.      Максимальная начальная скорость (максимальная начальная кинетическая энергия) фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой v.

III.     Для каждого вещества существует красная граница фотоэффекта, т. е. минимальная частота v₀ света (зависящая от химической природы вещества и состояния его поверхности), ниже которой фотоэффект невозможен.

Качественное объяснение фотоэффекта с волновой точки зрения на первый взгляд не должно было бы представлять трудностей. Действительно, под действием поля световой волны в металле возникают вынужденные колебания электронов, амплитуда которых (например, при резонансе) может быть достаточной для того, чтобы электроны покинули металл; тогда и наблюдается фотоэффект. Кинетическая энергия вырываемого из металла электрона должна была бы зависеть от интенсивности падающего света, так как с увеличением последней электрону передавалась бы большая энергия. Однако этот вывод противоречит II закону фотоэффекта. Так как, по волновой теории, энергия, передаваемая электронам, пропорциональна интенсивности света, то свет любой частоты, но достаточно большой интенсивности должен был бы вырывать электроны из металла; иными словами, красной границы фотоэффекта не должно быть, что противоречит III закону фотоэффекта. Кроме того, волновая теория не смогла объяснить безынерционность фотоэффекта, установленную опытами. Таким образом, фотоэффект необъясним с точки зрения волновой теории света.

1 2 3 4 5 6 7 8 9 ... 12