|
|
Закон Ампера. Закон БиоСавараЛапласа. Магнитная индукция прямого и кругового тока
§ 162. Дифференциальное уравнение электромагнитной волны
К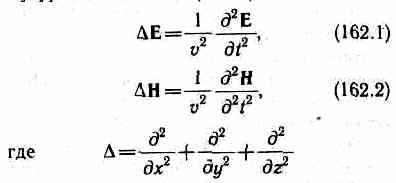 ак уже указывалось (см. §161), одним из важнейших следствий уравнений Максвелла (см. § 139) является существование электромагнитных волн. Можно показать, что для однородной и изотропной среды вдали от зарядов и токов, создающих электромагнитное поле, из уравнений Максвелла следует, что векторы напряженностей Е и Н переменного электромагнитного поля удовлетворяют волновому уравнению типа (154.9):— оператор Лапласа, v— фазовая скорость. ак уже указывалось (см. §161), одним из важнейших следствий уравнений Максвелла (см. § 139) является существование электромагнитных волн. Можно показать, что для однородной и изотропной среды вдали от зарядов и токов, создающих электромагнитное поле, из уравнений Максвелла следует, что векторы напряженностей Е и Н переменного электромагнитного поля удовлетворяют волновому уравнению типа (154.9):— оператор Лапласа, v— фазовая скорость.
В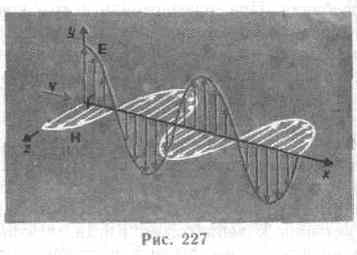 сякая функция, удовлетворяющая уравнениям (162.1) и (162.2), описывает некоторую волну. Следовательно, электромагнитные поля действительно могут существовать в виде электромагнитных волн. Фазовая скорость электромагнитных волн определяется выражением сякая функция, удовлетворяющая уравнениям (162.1) и (162.2), описывает некоторую волну. Следовательно, электромагнитные поля действительно могут существовать в виде электромагнитных волн. Фазовая скорость электромагнитных волн определяется выражением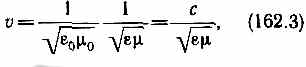
где с= 1/00, 0 и 0 — соответственно электрическая и магнитная постоянные, и — соответственно электрическая и магнитная проницаемости среды.
В вакууме (при =1 и =1) скорость распространения электромагнитных волн совпадает со скоростью с. Так как > 1, то скорость распространения электромагнитных волн в веществе всегда меньше, чем в вакууме.
При вычислении скорости распространения электромагнитного поля по формуле (162.3) получается результат, достаточно хорошо совпадающий с экспериментальными данными, если учитывать зависимость и , от частоты. Совпадение же размерного коэффициента в (162.3) со cкоростью распространения света в вакууме указывает на глубокую связь между электромагнитными и оптическими явлениями, позволившую Максвеллу создать электромагнитную теорию света, согласно которой свет представляет собой электромагнитные волны.
Следствием теории Максвелла является поперечность электромагнитных волн: векторы Е и Н напряженностей электрического и магнитного полей волны взаимно перпендикулярны (на рис. 227 показана моментальная «фотография» плоской электромагнитной волны) и лежат в плоскости, перпендикулярной вектору v скорости распространения волны, причем векторы Е, Н и v образуют правовинтовую систему. Из уравнений Максвелла следует также, что в электромагнитной волне векторы Е и Н всегда колеблются в одинаковых фазах (см. рис. 227), причем мгновенные значения £ и Я в любой точке связаны соотношением
0=0Н. (162.4) Следовательно, E и H одновременно достигают максимума, одновременно обращаются в нуль и т. д.  От волновых уравнений (162.1) и (162.2) можно перейти к уравнениям где соответственно индексы у и z при Е н Н подчеркивают лишь то, что векторы Е и Н направлены вдоль взаимно перпендикулярных осей у и z. От волновых уравнений (162.1) и (162.2) можно перейти к уравнениям где соответственно индексы у и z при Е н Н подчеркивают лишь то, что векторы Е и Н направлены вдоль взаимно перпендикулярных осей у и z.
Уравнениям (162.5) и (162.6) удовлетворяют, в частности, плоские монохроматические электромагнитные волны (электромагнитные волны одной строго определенной частоты), описываемые уравнениями Еу=Е0cos(t-kx+), (162.7) Hz= H0cos(t-kx+),(162.8)
где е0и Н0 — соответственно амплитуды напряженностей электрического и магнитного полей волны, — круговая частота волны, k=/v— волновое число, — начальные фазы колебаний в точках с координатой х=0. В уравнениях (162.7) и (162.8) одинаково, так как колебания электрического и магнитного векторов в электромагнитной волне происходят с одинаковой фазой.
§ 163. Энергия электромагнитных волн. Импульс электромагнитного поля Возможность обнаружения электромагнитных волн указывает на то, что они переносят энергию. Объемная плотность wэнергии электромагнитной волны складывается из объемных плотностей wэл (см. (95.8)) и wм(см. (130.3)) электрического и магнитного полей: w= wэл+wм=0E2/2+0H2/2.Учитывая выражение (162.4), получим, что плотность энергии электрического и магнитного полей в каждый момент времени одинакова, т. е. wэл = wм. Поэтому w=2wэл=0Е2 =00ЕН. Умножив плотность энергии wна скорость vраспространения волны в среде (см. (162.3)), получим модуль плотности потока энергии:
S=wv=EH. Так как векторы Е и Н взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему, то направление вектора [ЕН] совпадает с направлением переноса энергии, а модуль этого вектора равен ЕН. Вектор плотности потока электромагнитной энергии называется вектором Умова— Пойнтинга:
S = [EH].
Вектор S направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.
Если электромагнитные волны поглощаются или отражаются телами (эти явления подтверждены опытами Г. Герца), то из теории Максвелла следует, что электромагнитные волны должны оказывать на тела давление. Давление электромагнитных волн объясняется тем, что под действием электрического поля волны заряженные частицы вещества начинают упорядоченно двигаться и подвергаются со стороны магнитного поля волны действию сил Лоренца. Однако значение этого давления ничтожно. Можно оценить, что при средней мощности солнечного излучения, приходящего на Землю, давление для абсолютно поглощающей поверхности составляет примерно 5 мкПа. В исключительно тонких экспериментах, ставших классическими, П. Н. Лебедев в 1899 г. доказал существование светового давления на твердые тела, а в 1910г.— на газы. Опыты Лебедева имели огромное значение для утверждения выводов теории Максвелла о том, что свет представляет собой электромагнитные волны.
Существование давления электромагнитных волн приводит к выводу о том, что электромагнитному полю присущ механический импульс. Импульс электромагнитного поля
p=W/c,
где W— энергия электромагнитного поля. Выражая импульс как р=mc(поле в вакууме распространяется со скоростью с), получим p = mc=W/c, откуда
W = mc2. (163.1)
Это соотношение между массой и энергией свободного электромагнитного поля является универсальным законом природы (см. также §40). Согласно специальной теории относительности, выражение (163.1) имеет общее значение и справедливо для любых тел независимо от их внутреннего строения.
Таким образом, рассмотренные свойства электромагнитных волн, определяемые теорией Максвелла, полностью подтверждаются опытами Герца, Лебедева и выводами специальной теории относительности, сыгравшими решающую роль для подтверждения и быстрого признания этой теории.
§ 164. Излучение диполя. Применение электромагнитных волн
Простейшим излучателем электромагнитных волн является электрический диполь, электрический момент которого изменяется во времени по гармоническому закону р = р0cost, где р0 — амплитуда вектора р. Примером подобного диполя может служить система, состоящая из покоящегося положительного заряда +Q и отрицательного заряда -Q, гармонически колеблющегося вдоль направления р с частотой . Задача об излучении диполя имеет в теории излучающих систем важное значение, так как всякую реальную излучающую систему (например, антенну) можно рассчитывать рассматривая излучение диполя. Кроме того, многие вопросы взаимодействия излучения с веществом можно объяснить на основе классической теории, рассматривая атомы как системы зарядов, в которых электроны совершают гармонические колебания около их положений равновесия.
Характер электромагнитного поля диполя зависит от выбора рассматриваемой точки. Особый интерес представляет так называемая волновая зона диполя — точки пространства, отстоящие от диполя на расстояниях r, значительно превышающих длину волны (r>>),— так как в ней кар-
тина электромагнитного поля диполя сильно упрощается. Это связано с тем, что в волновой зоне диполя практически остаются только «отпочковавшиеся» от диполя, свободно распространяющиеся поля, в то время как поля, колеблющиеся вместе с диполем и имеющие более сложную структуру, сосредоточены в области расстояний r<=.
Если волна распространяется в однородной изотропной среде, то время прохождения волны до точек, удаленных от диполя на расстояние r, одинаково. Поэтому во всех точках сферы, центр которой совпадает с диполем, фаза колебаний одинакова, т. е. в волновой зоне волновой фронт будет сферическим и, следовательно, волна, излучаемая диполем, есть сферическая волна.
В каждой точке векторы Е и Н колеблются по закону cos(t-kr), амплитуды этих векторов пропорциональны 1/rsin
(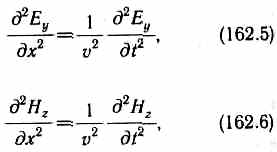 для вакуума), т. е. зависят от расстояния rдо излучателя и угла между направлением радиуса-вектора и осью диполя. Отсюда следует, что интенсивность излучения диполя в волновой зоне для вакуума), т. е. зависят от расстояния rдо излучателя и угла между направлением радиуса-вектора и осью диполя. Отсюда следует, что интенсивность излучения диполя в волновой зоне
Isin2/r2. (164.1)
З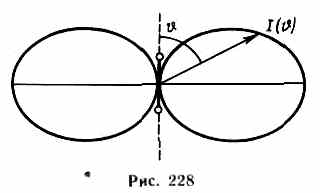 ависимость (164.1) I от при заданном значении r, приводимая в полярных координатах (рис.228), называется диаграммой направленности излучения диполя. Как видно из выражения (164.1) и приведенной диаграммы, диполь сильнее всего излучает в направлениях, перпендикулярных его оси (=/2). Вдоль своей оси (=0 и =) диполь не излучает вообще. Диаграмма направленности излучения диполя позволяет формировать излучение с определенными характеристиками и используется при конструировании антенн.Впервые электромагнитные волны были использованы через семь лет после опытов Герца. 7 мая 1895 г. преподаватель физики офицерских минных классов А.С.Попов (1859—1906) на заседании Русского физико-химического общества продемонстрировал первый в мире радиоприемник, открывший возможность практического использования электромагнитных волн для беспроволочной связи, преобразившей жизнь человечества. Первая переданная в мире радиограмма содержала лишь два слова: «Генрих Герц». Изобретение радио Поповым сыграло огромную роль в деле распространения и развития теории Максвелла. ависимость (164.1) I от при заданном значении r, приводимая в полярных координатах (рис.228), называется диаграммой направленности излучения диполя. Как видно из выражения (164.1) и приведенной диаграммы, диполь сильнее всего излучает в направлениях, перпендикулярных его оси (=/2). Вдоль своей оси (=0 и =) диполь не излучает вообще. Диаграмма направленности излучения диполя позволяет формировать излучение с определенными характеристиками и используется при конструировании антенн.Впервые электромагнитные волны были использованы через семь лет после опытов Герца. 7 мая 1895 г. преподаватель физики офицерских минных классов А.С.Попов (1859—1906) на заседании Русского физико-химического общества продемонстрировал первый в мире радиоприемник, открывший возможность практического использования электромагнитных волн для беспроволочной связи, преобразившей жизнь человечества. Первая переданная в мире радиограмма содержала лишь два слова: «Генрих Герц». Изобретение радио Поповым сыграло огромную роль в деле распространения и развития теории Максвелла.
Электромагнитные волны сантиметрового и миллиметрового диапазонов, встречая на своем пути преграды, отражаются от них. Это явление лежит в основе радиолокации — обнаружения предметов (например, самолетов, кораблей и т. д.) на больших расстояниях и точного определения их положения. Помимо этого, методы радиолокации используются для наблюдения прохождения и образования облаков, движения метеоритов в верхних слоях атмосферы и т. д.Для электромагнитных волн характерно явление дифракции — огибания волнами различных препятствий. Именно благодаря дифракции радиоволн возможна устойчивая радиосвязь между удаленными пунктами, разделенными между собой выпуклостью Земли. Длинные волны (сотни и тысячи метров) применяются в фототелеграфии, короткие волны (несколько метров и меньше) применяются в телевидении для передачи изображений на небольшие расстояния (немногим больше пределов прямой видимости). Электромагнитные волны используются также в радиогеодезии для очень точного определения расстояний с помощью радиосигналов, в радиоастрономии для исследования радиоизлучения небесных тел и т. д. Полное описание применения электромагнитных волн дать практически невозможно, так как нет областей науки и техники, где бы они не использовались.
№16 Одномерная потенциальная ступень(порог). Коэффициент отражения прохождения(прозрачности).
Рассмотрим простейший потенциальный барьер прямоугольной формы (рис. 298, а)для одномерного (по оси х) движения частицы. Для потенциального барьера прямоугольной формы высоты U и ширины lможем записать
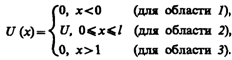
П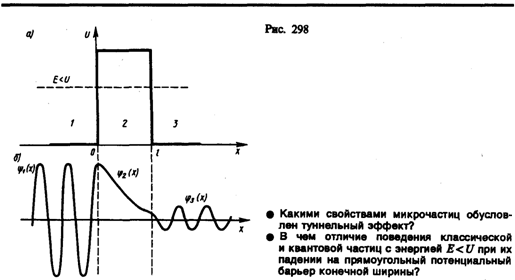 ри данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером (при Е>U), либо отразится от него (приЕи будет двигаться в обратную сторону, т. е. она не может проникнуть сквозь барьер. Для микрочастицы же, даже при Е>U, имеется отличная от нуля вероятность, что частица отразится от барьера и будет двигаться в обратную сторону. При E<Uимеется также отличная от нуля вероятность, что частица окажется в области х>1,т. е. проникает сквозь барьер. Подобные, казалось бы, парадоксальные выводы следуют непосредственно из решения уравнения Шредингера, описывающего движение микрочастицы при условиях данной задачи.Уравнение Шредингера (217.5) для стационарных состояний для каждой из выделенных на рис. 298, а области имеет вид ри данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером (при Е>U), либо отразится от него (приЕи будет двигаться в обратную сторону, т. е. она не может проникнуть сквозь барьер. Для микрочастицы же, даже при Е>U, имеется отличная от нуля вероятность, что частица отразится от барьера и будет двигаться в обратную сторону. При E<Uимеется также отличная от нуля вероятность, что частица окажется в области х>1,т. е. проникает сквозь барьер. Подобные, казалось бы, парадоксальные выводы следуют непосредственно из решения уравнения Шредингера, описывающего движение микрочастицы при условиях данной задачи.Уравнение Шредингера (217.5) для стационарных состояний для каждой из выделенных на рис. 298, а области имеет вид (221.1) (221.1)
Общие решения этих дифференциальных уравнений: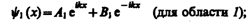 (221.2) (221.2) 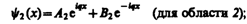 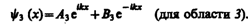 (221.3) (221.3)
В частности, для области 1 полная волновая функция, согласно (217.4), будет иметь вид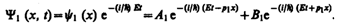 (221.4) (221.4)
В этом выражении первый член представляет собой плоскую волну типа (219.3), распространяющуюся в положительном направлении оси х (соответствует частице, движущейся в сторону барьера), а второй — волну, распространяющуюся в противоположном направлении, т. е. отраженную от барьера (соответствует частице, движущейся от барьера налево).
Решение (221.3) содержит также волны (после умножения на временной множитель), распространяющиеся в обе стороны. Однако в области 3 имеется только волна, прошедшая сквозь барьер и распространяющаяся слева направо. Поэтому коэффициент B3 в формуле (221.3) следует принять равным нулю.
В области 2 решение зависит от соотношений Е>U или Е<U. Физический интерес представляет случай, когда полная энергия частицы меньше высоты потенциального барьера, поскольку при Е<U законы классической физика однозначно не разрешают частице проникнуть сквозь барьер. В данном случае, согласно (221.1), q=ib— мнимое число, где
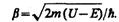
Учитывая значение q и B3=0, получим решения уравнения Шредингера для трех областей в следующем виде: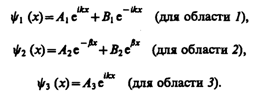 (221.5)В области 2 функция (221.5) уже не соответствует плоским волнам, распространяющимся в обе стороны, поскольку показатели степени экспонент не мнимые, а действительные. Можно показать, что для частного случая высокого и широкого барьера, когда bl>>1, B2»0. (221.5)В области 2 функция (221.5) уже не соответствует плоским волнам, распространяющимся в обе стороны, поскольку показатели степени экспонент не мнимые, а действительные. Можно показать, что для частного случая высокого и широкого барьера, когда bl>>1, B2»0.
Качественный характер функций y1(х),y2(х) и y3(x) иллюстрируется на рис. 298, б,откуда следует, что волновая функция не равна нулю и внутри барьера, а в области 3,если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же импульсом, т. е. с той же частотой, но с меньшей амплитудой. Следовательно, получили, что частица имеет отличную от нудя вероятность прохождения сквозь потенциальный барьер конечной ширины.Таким образом, квантовая механика приводит к принципиально новому специфическому квантовому явлению, получившему название туннельного эффекта, в результате которого микрообъект может «пройти» сквозь потенциальный барьер.Для описания туннельного эффекта используют понятиекоэффициента прозрачности D потенциального барьера, определяемого как отношение плотности потока прошедших частиц к плотности потока падающих. Можно показать, что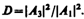 Для того чтобы найти отношение |А3/А1|2, необходимо воспользоваться условиями непрерывности y и y' на границах барьера х=0 и х=l (рис. 298): Для того чтобы найти отношение |А3/А1|2, необходимо воспользоваться условиями непрерывности y и y' на границах барьера х=0 и х=l (рис. 298):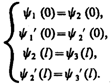 (221.6)Эти четыре условия дают возможность выразить коэффициенты A2,A3, В1 и В2 через А1.Совместное решение уравнений (221.6) для прямоугольного потенциального барьера дает (в предположении, что коэффициент прозрачности мал по сравнению с единицей) (221.6)Эти четыре условия дают возможность выразить коэффициенты A2,A3, В1 и В2 через А1.Совместное решение уравнений (221.6) для прямоугольного потенциального барьера дает (в предположении, что коэффициент прозрачности мал по сравнению с единицей) 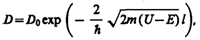 (221.7) где U— высота потенциального барьера, Е — энергия частицы, l — ширина барьера, D0— постоянный множитель, который можно приравнять единице. Из выражения (221.7) следует, что D сильно зависит от массы т частицы, ширины l барьера и от (U—E); чем шире барьер, тем меньше вероятность прохождения сквозь него частицы. Для потенциального барьера произвольной формы (рис. 299), удовлетворяющей условиям так называемого квазиклассического приближения (достаточно гладкая форма кривой), имеем (221.7) где U— высота потенциального барьера, Е — энергия частицы, l — ширина барьера, D0— постоянный множитель, который можно приравнять единице. Из выражения (221.7) следует, что D сильно зависит от массы т частицы, ширины l барьера и от (U—E); чем шире барьер, тем меньше вероятность прохождения сквозь него частицы. Для потенциального барьера произвольной формы (рис. 299), удовлетворяющей условиям так называемого квазиклассического приближения (достаточно гладкая форма кривой), имеем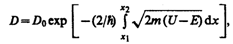
г де U=U(x).С классической точки зрения прохождение частицы сквозь потенциальный барьер при Е<U невозможно, так как частица, находясь в области барьера, должна была бы обладать отрицательной кинетической энергией. Туннельный эффект является специфическим квантовым эффектом. Прохождение частицы сквозь область, в которую, согласно законам классической механики, она не может проникнуть, можно пояснить соотношением неопределенностей. Неопределенность импульса Dр на отрезке Dх=l составляет Dp>h/l. Связанная с этим разбросом в значениях импульса кинетическая энергия (Dр)2/(2m) может оказаться достаточной для того, чтобы полная энергия частицы оказалась больше потенциальной.Основы теории туннельных переходов заложены работами Л. И. Мандельштама и М. А. Леонтовича (1903—1981). Туннельное прохождение сквозь потенциальный барьер лежит в основе многих явлений физики твердого тела (например, явления в контактном слое на границе двух полупроводников), атомной и ядерной физики (например, a-распад, протекание термоядерных реакций). де U=U(x).С классической точки зрения прохождение частицы сквозь потенциальный барьер при Е<U невозможно, так как частица, находясь в области барьера, должна была бы обладать отрицательной кинетической энергией. Туннельный эффект является специфическим квантовым эффектом. Прохождение частицы сквозь область, в которую, согласно законам классической механики, она не может проникнуть, можно пояснить соотношением неопределенностей. Неопределенность импульса Dр на отрезке Dх=l составляет Dp>h/l. Связанная с этим разбросом в значениях импульса кинетическая энергия (Dр)2/(2m) может оказаться достаточной для того, чтобы полная энергия частицы оказалась больше потенциальной.Основы теории туннельных переходов заложены работами Л. И. Мандельштама и М. А. Леонтовича (1903—1981). Туннельное прохождение сквозь потенциальный барьер лежит в основе многих явлений физики твердого тела (например, явления в контактном слое на границе двух полупроводников), атомной и ядерной физики (например, a-распад, протекание термоядерных реакций).
№17 Электромагнитная природа света. Поперечность электромагнитных волн. Монохроматические волны. Когерентность. Методы получения когерентных источников. Условия усиления и ослабления света при интереференции.
|
|
|
 Скачать 2.54 Mb.
Скачать 2.54 Mb. ависимость (164.1) I от при заданном значении r, приводимая в полярных координатах (рис.228), называется диаграммой направленности излучения диполя. Как видно из выражения (164.1) и приведенной диаграммы, диполь сильнее всего излучает в направлениях, перпендикулярных его оси (=/2). Вдоль своей оси (=0 и =) диполь не излучает вообще. Диаграмма направленности излучения диполя позволяет формировать излучение с определенными характеристиками и используется при конструировании антенн.Впервые электромагнитные волны были использованы через семь лет после опытов Герца. 7 мая 1895 г. преподаватель физики офицерских минных классов А.С.Попов (1859—1906) на заседании Русского физико-химического общества продемонстрировал первый в мире радиоприемник, открывший возможность практического использования электромагнитных волн для беспроволочной связи, преобразившей жизнь человечества. Первая переданная в мире радиограмма содержала лишь два слова: «Генрих Герц». Изобретение радио Поповым сыграло огромную роль в деле распространения и развития теории Максвелла.
ависимость (164.1) I от при заданном значении r, приводимая в полярных координатах (рис.228), называется диаграммой направленности излучения диполя. Как видно из выражения (164.1) и приведенной диаграммы, диполь сильнее всего излучает в направлениях, перпендикулярных его оси (=/2). Вдоль своей оси (=0 и =) диполь не излучает вообще. Диаграмма направленности излучения диполя позволяет формировать излучение с определенными характеристиками и используется при конструировании антенн.Впервые электромагнитные волны были использованы через семь лет после опытов Герца. 7 мая 1895 г. преподаватель физики офицерских минных классов А.С.Попов (1859—1906) на заседании Русского физико-химического общества продемонстрировал первый в мире радиоприемник, открывший возможность практического использования электромагнитных волн для беспроволочной связи, преобразившей жизнь человечества. Первая переданная в мире радиограмма содержала лишь два слова: «Генрих Герц». Изобретение радио Поповым сыграло огромную роль в деле распространения и развития теории Максвелла. ри данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером (при Е>U), либо отразится от него (приЕ
ри данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером (при Е>U), либо отразится от него (приЕ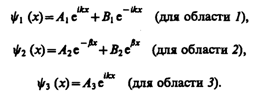 (221.5)В области 2 функция (221.5) уже не соответствует плоским волнам, распространяющимся в обе стороны, поскольку показатели степени экспонент не мнимые, а действительные. Можно показать, что для частного случая высокого и широкого барьера, когда bl>>1, B2»0.
(221.5)В области 2 функция (221.5) уже не соответствует плоским волнам, распространяющимся в обе стороны, поскольку показатели степени экспонент не мнимые, а действительные. Можно показать, что для частного случая высокого и широкого барьера, когда bl>>1, B2»0. де U=U(x).С классической точки зрения прохождение частицы сквозь потенциальный барьер при Е<U невозможно, так как частица, находясь в области барьера, должна была бы обладать отрицательной кинетической энергией. Туннельный эффект является специфическим квантовым эффектом. Прохождение частицы сквозь область, в которую, согласно законам классической механики, она не может проникнуть, можно пояснить соотношением неопределенностей. Неопределенность импульса Dр на отрезке Dх=l составляет Dp>h/l. Связанная с этим разбросом в значениях импульса кинетическая энергия (Dр)2/(2m) может оказаться достаточной для того, чтобы полная энергия частицы оказалась больше потенциальной.Основы теории туннельных переходов заложены работами Л. И. Мандельштама и М. А. Леонтовича (1903—1981). Туннельное прохождение сквозь потенциальный барьер лежит в основе многих явлений физики твердого тела (например, явления в контактном слое на границе двух полупроводников), атомной и ядерной физики (например, a-распад, протекание термоядерных реакций).
де U=U(x).С классической точки зрения прохождение частицы сквозь потенциальный барьер при Е<U невозможно, так как частица, находясь в области барьера, должна была бы обладать отрицательной кинетической энергией. Туннельный эффект является специфическим квантовым эффектом. Прохождение частицы сквозь область, в которую, согласно законам классической механики, она не может проникнуть, можно пояснить соотношением неопределенностей. Неопределенность импульса Dр на отрезке Dх=l составляет Dp>h/l. Связанная с этим разбросом в значениях импульса кинетическая энергия (Dр)2/(2m) может оказаться достаточной для того, чтобы полная энергия частицы оказалась больше потенциальной.Основы теории туннельных переходов заложены работами Л. И. Мандельштама и М. А. Леонтовича (1903—1981). Туннельное прохождение сквозь потенциальный барьер лежит в основе многих явлений физики твердого тела (например, явления в контактном слое на границе двух полупроводников), атомной и ядерной физики (например, a-распад, протекание термоядерных реакций).
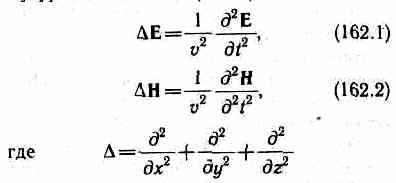 ак уже указывалось (см. §161), одним из важнейших следствий уравнений Максвелла (см. § 139) является существование электромагнитных волн. Можно показать, что для однородной и изотропной среды вдали от зарядов и токов, создающих электромагнитное поле, из уравнений Максвелла следует, что векторы напряженностей Е и Н переменного электромагнитного поля удовлетворяют волновому уравнению типа (154.9):— оператор Лапласа, v— фазовая скорость.
ак уже указывалось (см. §161), одним из важнейших следствий уравнений Максвелла (см. § 139) является существование электромагнитных волн. Можно показать, что для однородной и изотропной среды вдали от зарядов и токов, создающих электромагнитное поле, из уравнений Максвелла следует, что векторы напряженностей Е и Н переменного электромагнитного поля удовлетворяют волновому уравнению типа (154.9):— оператор Лапласа, v— фазовая скорость. сякая функция, удовлетворяющая уравнениям (162.1) и (162.2), описывает некоторую волну. Следовательно, электромагнитные поля действительно могут существовать в виде электромагнитных волн. Фазовая скорость электромагнитных волн определяется выражением
сякая функция, удовлетворяющая уравнениям (162.1) и (162.2), описывает некоторую волну. Следовательно, электромагнитные поля действительно могут существовать в виде электромагнитных волн. Фазовая скорость электромагнитных волн определяется выражением От волновых уравнений (162.1) и (162.2) можно перейти к уравнениям где соответственно индексы у и z при Е н Н подчеркивают лишь то, что векторы Е и Н направлены вдоль взаимно перпендикулярных осей у и z.
От волновых уравнений (162.1) и (162.2) можно перейти к уравнениям где соответственно индексы у и z при Е н Н подчеркивают лишь то, что векторы Е и Н направлены вдоль взаимно перпендикулярных осей у и z.