АИСД. АиСД Л.Р. 1. 1. Введение 1 Цель работы

• Название: 1. Введение 1 Цель работы
• Дата: 21.12.2021
• Размер: 327.5 Kb.
• Имя файла: АиСД Л.Р. 1.doc
• Тип: Документы; #312844

1.Введение

1.1 Цель работы

Цель работы: получить навыки работы в системе статистиче­ского анализа и визуализации данных R.

Описание системы R.

R — язык программирования для статистической обработки данных и рабо­ты с графикой, а также свободная программная среда вычислений с открытым ис­ходным кодом.

Изначально R был разработан сотрудниками статистического факультета Оклендского университета Россом Айхэкой (англ. Ross Ihaka) и Робертом Джентлменом (англ. Robert Gentleman). Язык и среда исполнения поддерживаются и развиваются организацией «R Foundation».

R широко используется как статистическое программное обеспечение для анализа данных и фактически стал стандартом для статистических программ.

В R используется интерфейс командной строки, хотя доступны и несколько графических интерфейсов пользователя, например пакет R Commander, RКWard, RStudio, Weka, Rapid Miner. KNIME, а также средства интеграции в офисные па­кеты.

R поддерживает широкий спектр статистических и численных методов и обладает хорошей расширяемостью с помощью пакетов. Пакеты представляют собой библиотеки для работы специфических функций или специальных областей применения. В базовую поставку R включен основной набор пакетов, а всего по состоянию на 2017 год доступно более 11778 пакетов.

Ещё одной особенностью R являются графические возможности, заклю­чающиеся в возможности создания качественной графики, которая может вклю­чать математические символы.

2. Постановка задачи

2.1. Задача 1

Сгенерируйте вектор длины N=1000, элементами которого являются реализации нормально распределенной случайной величины с математическим ожиданием, равным 1, и стандартным отклонением, равным 0.3.

Подсчитайте статистическое мат. ожидание и стандартную ошибку, не используя встроенные функции и проверьте правильность результата. Подсчитайте .95,.99-квантили.

Исследуйте отклонение статистического мат. ожидания от 1 при росте N (N=1000,2000,4000,8000).

2.2. Задача 2

Создайте фрейм данных из N=20 записей со следующими полями: Nrow — номер записи, Name — имя пользователя, BirthYear — год рождения, EmployYear — год приема на работу, Salary — зарплата, где Nrow изменяется от 1 до N, Name задается произвольно, BithYear распределен равномерно на отрезке [1960,1985], EmployYear распределен равномерно на отрезке [BirthYear+18,2006], Salary для работников младше 1975 г.р. определяется по формуле Salary=(ln(2007-EmployYear)+1)*8000, для остальных Salary=(log2(2007-EmployYear)+1)*8000.

Подсчитайте число сотрудников с зарплатой, большей 15000. Добавьте в таблицу поле, соответствующее суммарному подоходному налогу (ставка 13%), выплаченному сотрудником за время работы в организации, если его зарплата за каждый код начислялась согласно формулам для Salary, где вместо 2007 следует последовательно подставить каждый год работы сотрудника в организации.

2.3 Задача 3

Напишите функцию, которая принимает на вход числовой вектор x и число разбиений интервала k (по умолчанию равное числу элементов вектора, разделенному на 10) и выполняет следующее: находит минимальное и максимальное значение элементов вектора xmin и xmax, разделяет полученный отрезок [xmin;xmax] на k равных интервалов и подсчитывает число элементов вектора, принадлежащих каждому интервалу.

Далее должен строиться график, где по оси абсцисс — середины интервалов, по оси ординат — число элементов вектора, принадлежащих интервалу, разделенное на общее число точек.

Проведите эксперимент на данной функции, где x — вектор длины 5000, сгенерированный из экспоненциально распределенной случайной величины,k=500. Приближение какого графика мы получаем в итоге при большом числе точек и числе разбиений?

2.4 Задача 4

Необходимо проектировать и реализовать метод наименьших квадратов.

3. Ход работы

Для выполнения данной лабораторной работы использовалась IDE Rstudio, а также пакет R версии 3.3.1 для Microsoft Windows 7 (х64).

3.1 Решение задачи №1.

Квантиль в математической статистике — значение, которое заданная случайная величина не превышает, с фиксированной вероятностью.

Математическое ожидание — среднее значение случайной величины (распределение вероятностей случайной величины, рассматривается в теории вероятностей).

Стандартная ошибка среднего в математической статистике - величина, характеризующая стандартное отклонение выборочного среднего, рассчитанное по выборке размера n из генеральной совокупности.

Специальной функции для расчета стандартной ошибки средней в R нет, однако для этого подходят уже имеющиеся функции. Как известно, стандартная ошибка средней рассчитывается как отношение стандартного отклонения к квад­ратному корню из объема выборки.

Для реализации нормально распределенной случайной величины с матема­тическим ожиданием, равным 1, и стандартным отклонением, равным 0.3 исполь­зуем функцию rnorm с параметрами mean =1, sd = 0.3

Исходный код программы на R:

K1 = 1000 #Инициализация переменных

#Для расчета заданной функции воспользуемся

#такими величинами, как мат.ожидание, равное 1

#и стандартное отклонение, равное 0.3

X = rnorm(K1, mean = 1, sd = 0.3)

X = sort(X, decreasing = FALSE) # сортируем полученный массив

#посчитаем мат. ожидание как среднее арифметическое

Sum = 0

for(i in 1:K1)

{

Sum = Sum + X[i];

}

N1 = Sum / K1; #стат. мат. ожидание

N1

#Расчет стандартной ошибки

Stderr = 1-N1

Stderr

#Расчет квантилей

K195 = X[K1 * 0.95]

K195

K199 = X[K1 * 0.99]

K199

Результаты, полученные после запуска данного кода в среде R: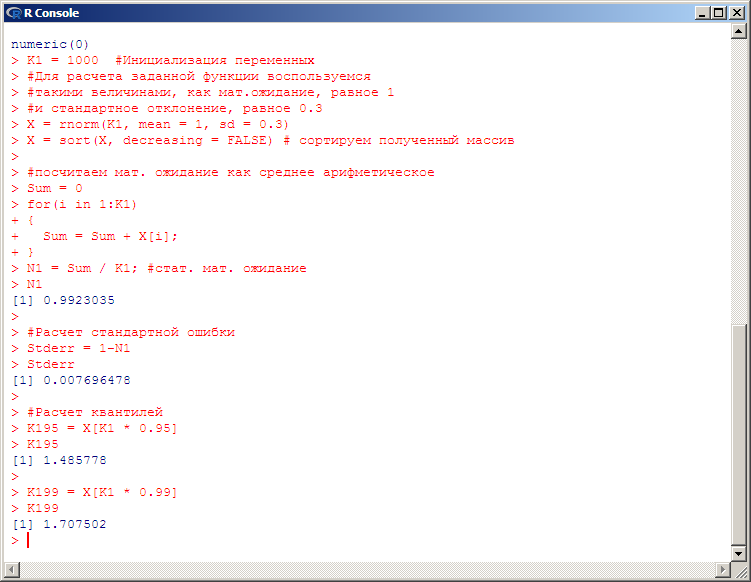



Вывод: как можно заметить из приведённых данных, статистическое мат. Ожидание с учетом параметров задачи стремится к 1 при увеличении N.

3.2. Решение задачи №2

Фреймы данных (data frames) —один из самых важных типов, данных в R, позволяющий объединять данные разных типов вместе. Можно считать, что фрейм данных — это таблица, в которой (в отличие от числовых матриц). Разные столбцы могут содержать данные разных типов (но все данные в одном столоне имеют один тип). Например, такая таблица может содержать результаты экспери­мента. Создать фрейм данных можно с помощью функции data.frame:

frm <- data.frame(data1, data2, …)

Здесь многоточие означает, что список данных может содержать произвольное число элементов. В качестве данных (data1, data2, …)

могут высту­пать векторы (числовые, символьные или логические), факторы, матрицы (число­вые, символьные или логические), списки или другие фреймы. При этом все век­торы должны иметь одинаковую длину, а матрицы и фреймы — одинаковое (та­кое же) число строк. Могут также встречаться векторы, длина которых меньше, но в этом случае их длина должна являться делителем максимальной встречаю­щейся длины. То же требование предъявляется к компонентам списков. Функция data.frame просто собирает все данные вместе. Символьные векторы конверти­руются в факторы. Остальные данные собираются во фрейм как есть.

Программа начинается с создания таблицы указанной в п.2.2, структуры, которой имеется 20 записей.

Для формирования фрейма выполняется следующая команда:

p <- data.frame(NRow,Name,BirthYear,EmployYear,Salary)

Для того, чтобы вывести на экран количество сотрудников с зарплатой, более 15000 выполняется команда print(sum(Salary>15000)).

Процесс создания фрейма и вывода вышеуказанной информации представлен ниже:

N = 20

NRow = (1:N)

Name = c("Ivanov","Smirnov","Kuznetsov","Popov","Sokolov",

"Petrov","Vasilyev","Mikhailov","Novikov","Fedorov", "Morozov","Volkov","Alekseev","Lebedev","Semenov","Egorov",

"Pavlov","Kozlov","Stepanov","Nikolaev")

BirthYear = trunc(runif(20, min=1960,max=1987))

EmployYear = trunc(runif(20, min=BirthYear+18,max=2006))

Salary <- c(ifelse(BirthYear>1975, (Salary=log(2007-EmployYear) + 1)*8000,

(Salary = log2(2007-EmployYear)+1)*8000))

p <- data.frame(NRow,Name,BirthYear,EmployYear,Salary)

print(sum(Salary>15000))

Далее выполняется создание в таблице дополнительного поля «Total» для отображения суммарного подоходного налога (13%), выплаченному сотрудником время работы в организации, если его зарплата за каждый год начислялась согласно формулам для Salary. Для этого в программу добавляется следующий код:

print(sum(Salary>15000)) #количество сотрудников с зарплатой более 15000

Total = (2007-EmployYear)*(Salary*0.13)

P <- data.frame(NRow,Name,BirthYear,EmployYear,Salary,Total)

Результаты исполнения программы с вышеуказанными дополнениями представлены на рисунке: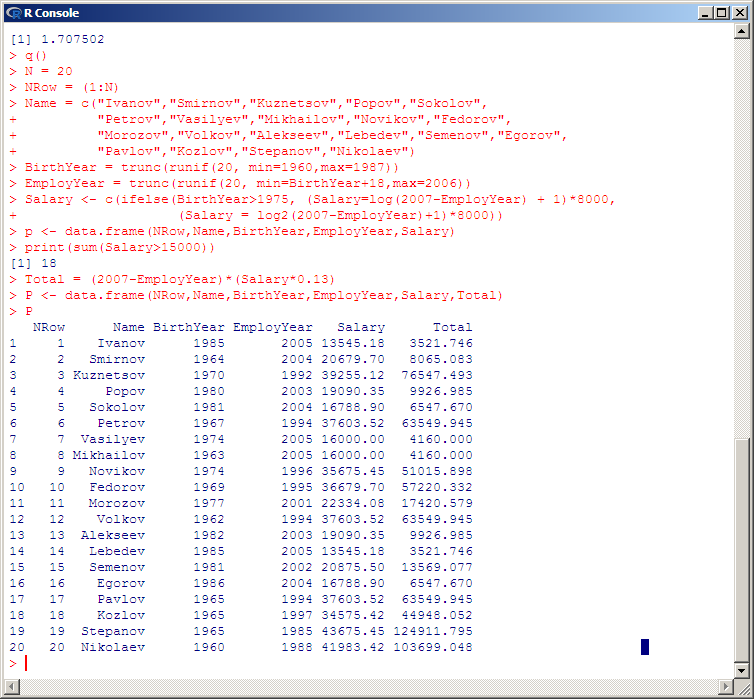



Полный исходный код программы:

N = 20

NRow = (1:N)

Name = c("Ivanov","Smirnov","Kuznetsov","Popov","Sokolov", "Petrov","Vasilyev","Mikhailov","Novikov","Fedorov", "Morozov","Volkov","Alekseev","Lebedev","Semenov","Egorov",

"Pavlov","Kozlov","Stepanov","Nikolaev")

BirthYear = trunc(runif(20, min=1960,max=1987))

EmployYear = trunc(runif(20, min=BirthYear+18,max=2006))

Salary <- c(ifelse(BirthYear>1975, (Salary=log(2007-EmployYear) + 1)*8000,

(Salary = log2(2007-EmployYear)+1)*8000))

p <- data.frame(NRow,Name,BirthYear,EmployYear,Salary)

print(sum(Salary>15000))

Total = (2007-EmployYear)*(Salary*0.13)

P <- data.frame(NRow,Name,BirthYear,EmployYear,Salary,Total)

P

Вывод: фреймы данных в R являются мощным и многофункциональным инструментом для анализа структурированных массивов информации.

3.3. Решение задачи №3

Для решения данного задания была написана функция, которая принимает на вход вектор сгенерированный из экспоненциально распределенной случайной величины (встроенная функция rexp). Также использовалась встроенная функция seq и цикл for.

Исходный код:

#создаем функцию с именем vec, которая принимает на входе вектор X и число разбиений k (можно не указывать),

#тогда k будет равно числу элементов вектора X, разделенному нацело на 10(возвращает часть от деления).

vec = function(x,k=(length(x)%/%10)) {

#Находим минимальное значение исходного вектора

xmin = min(x)

#находим максимальное значение исходного вектора

xmax = max(x)

#Создаем вектор от минимального до максимального элементов длиной k+1(чтобы интервалов было ровно k)

vect=seq(xmin,xmax,len = k+1)

#Создаем вектор для хранения кол-ва элементов в каждом интервале

interval=c()

#Создаем вектор для хранения значений середины каждого из интервалов

interval_mean=c()

#Циклом проходим вектор X

for(i in c(1:k)) {

#Считаем количество элементов вектора X, которые больше i-го элемента и меньше [i+1] элемента вектора vec

interval[i] = length(x[x>vect[i] & x < vect[i+1]])

#Нахожу среднее арифметическое между одним элементом и следующим чтоб найти середину этого интервала(между i и [i+1] элемента вектора vec

interval_mean[i] = mean(c(vect[i],vect[i+1]))

}

#Строим график, где по оси абсцисс - середины интервалов, а по oси ординат – число элементов вектора, принадлежащих интервалу разделенное на общее число точек

plot(interval_mean,(interval/sum(interval)))

#Interval, который содержит количество элементов вектора, принадлежащих каждому интервалу

print("Количество элементов вектора, принадлежащих каждому интервалу")

return(interval)

}

Данная функция строит график согласно заданию и выводит вектор который содержит количество элементов вектора, принадлежащих каждому интервалу.

Вызов функции в интерпретаторе выглядит следующим образом

vec(rexp(5000))

Полученные результаты представлены на рисунках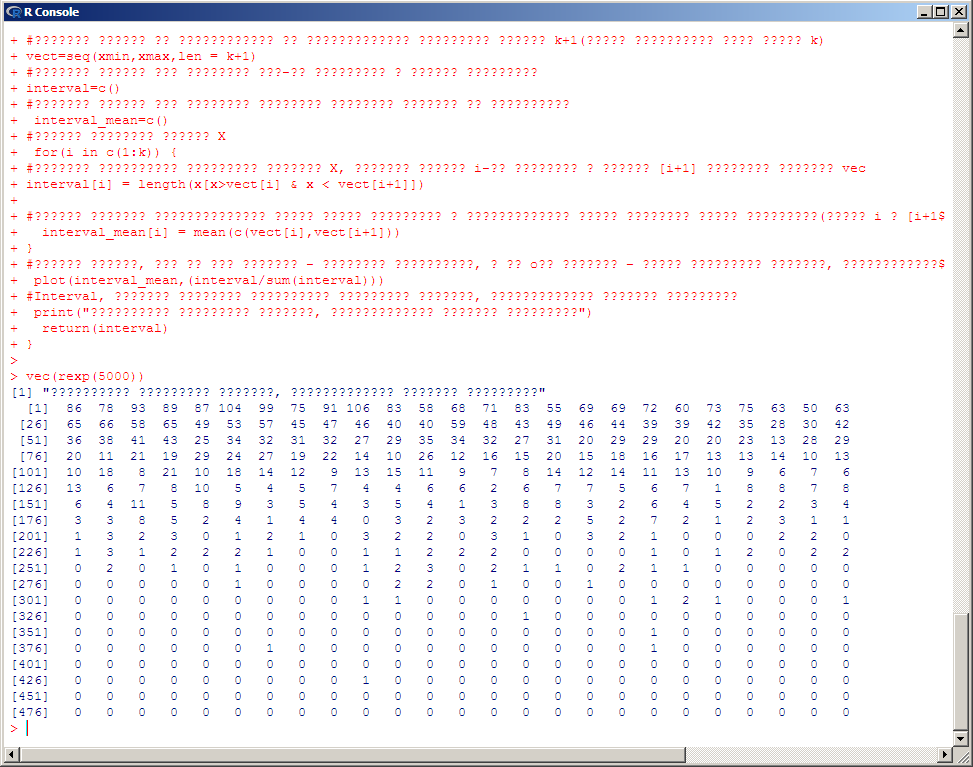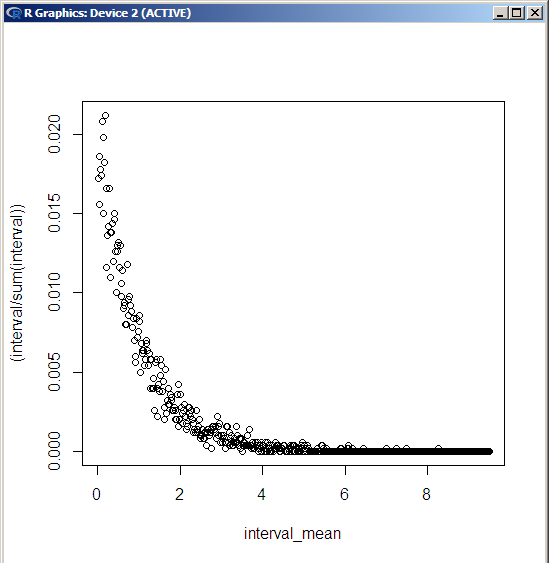





Вывод построенный график приближен к функции y=k/x, где k>0.

3.4. Решение задачи №4

Метод наименьших квадратов — это математическая процедура составления линейного уравнения, максимально соответствующего набору упорядочен­ных пар, путем нахождения значений для a и b, коэффициентов в уравнении прямой.

Цель метода наименьших квадратов состоит в минимизации общей квадратичной ошибки между значениями y и . Если для каждой точки мы определяем ошибку y’, метод наименьших квадратов минимизируется:



где n - число упорядоченных пар вокруг линии, максимально соответствующей данным.

Для примера возьмём два вектора с 5 элементами в каждом x и y.

С помощью метода наименьших квадратов определяем уравнение, максимально соответствующее данным, путем вычисления значений a, отрезка на оси y, и b, наклона линии:





где xср — среднее значение х, независимой переменной, уср — среднее значение у, независимой переменной.

В таблице ниже суммированы необходимые для этих уравнений вычисления.

x	y	xy	x2	y2
2	3	6	4	9
4	10	40	16	100
5	5	25	25	25
6	8	48	36	64
8	9	72	64	81

Ход вычисления коэффициентов результирующего уравнения представлен на последующих формулах:











Кривая эффекта для нашего примера будет определяться следующим уравнением:



Исходный код, реализующий данный метод представлен ниже:

#произвольно генерируем вектор x с произвольным количеством элементов

x=sample(1:30, sample(1:15,1))

x

size<-length(x) #количество элементов в векторе x

#произвольно генерируем вектор y с такой же длинной, как вектор x

y<-sample(1:30,size)

y

sumx=sum(x) #сумма элементов вектора x

sumy=sum(y) #сумма элементов вектора y

xy<-x*y #cсоздаем новый вектор из произведения элементов векторов x и y

xx<-x*x#cсоздаем новый вектор из произведения элементов векторов x

yy<-y*y#cсоздаем новый вектор из произведения элементов векторов y

sumxx=sum(xx) #сумма элементов вектора xx

sumyy=sum(y) #сумма элементов вектора yy

sumxy=sum(xy) #сумма элементов вектора xy

xy

xx

yy

sumxy

sumx

sumy

b=((size*sumxy)-(sumx*sumy))/((size*sumxx)-(sumx*sumx))#вычисляем наклон линии

b

xcr=sumx/size#среднее x

xcr

ycr=sumy/size#среднее y

ycr

a=ycr-xcr

a

Результаты работы: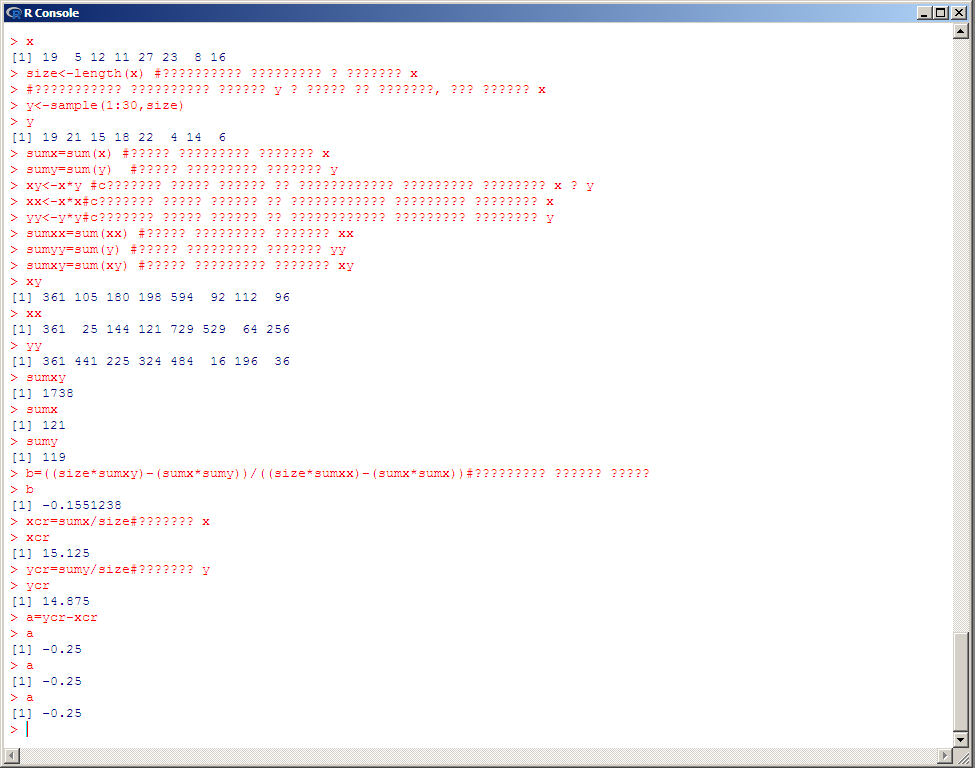



Вывод: метод наименьших квадратов является достаточно простым и эффективным методом определения уравнения, способного описать соотношение двух наборов данных. Это можно использовать при реализации различного рода методов компьютерного прогнозирования.

4. Заключение.

В процессе выполнения лабораторной работы мы приобрели навыки работы со средой использования языка R и IDE RStudio, мы узнали, какие бывают типы данных, в языке R и приобрели навыки обработки информации при помощи данных инструментов для вычисления разнообразных задач.