Лекции. 1. Введение. 1 Предмет гидравлики и краткая история её развития
 Скачать 1.38 Mb. Скачать 1.38 Mb.
|
|
В). Сопротивление растяжению внутри капельных жидкостей по молекулярной' теории может быть весьма значительным. При опытах с тщательно очищенной и Дегазированной водой В ней были получены кратковременные напряжения растяжения до 23 — 28 МПа. Однако технически чистые жидкости, содержащие взвешенные твердые частицы и мельчайшие пузырьки газов, не выдерживают даже незначительных напряжений растяжения. Поэтому в дальнейшем будем считать, что напряжения растяжения в капельных жидкостях невозможны. Г). На поверхности раздела жидкости и газа действуют силы поверхностного натяжения, стремящиеся придать объему жидкости сферическую форму и вызывающие некоторое дополнительное давление. Однако это давление заметно сказывается лишь при малых объемах жидкости и для сферических объемов (капель) определяется формулой 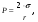 где σ — коэффициент поверхностного натяжения жидкости; r- радиус сферы. Коэффициент σ имеет следующие значения (Н/м) для разных жидкостей, граничащих с воздухом при температуре 20 °С: для, воды 73-3, спирта 22,5-3, керосина 27-3, ртути 460*10-3. С ростом температуры поверхностное натяжение уменьшается. В трубках малого диаметра дополнительное давление, обусловленное поверхностным натяжением, вызывает подъем (или опускание) жидкости относительно нормального уровня, характеризующий капиллярность жидкости. Высоту подъема смачивающей жидкости (или опускание, несмачивающей жидкости) в стеклянной трубке диаметром dопределяют по формуле для полусферического мениска 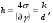 (1.17) (1.17)где k (мм2) имеет следующие значения: для воды +30, ртути - 10,1; спирта +11,5. С явлением капиллярности приходится сталкиваться при использовании стеклянных трубок в приборах для измерения давления, а также в некоторых случаях истечения жидкости. Большое значение приобретают силы поверхностного натяжения в жидкости, находящейся в условиях невесомости. 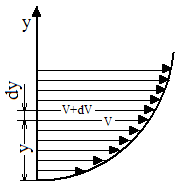 Рис.1.3 Течении вязкой жидкости вдоль твердой стенки Д). Вязкость представляет собой свойство жидкости сопротивляться сдвигу (скольжению) ее слоев. Это свойство проявляется в том, что в жидкости при определенных условиях возникают касательные напряжения. Вязкость есть свойство, противоположное текучести: более вязкие жидкости (глицерин, смазочные масла и др.) являются менее текучими, и наоборот. При течении вязкой жидкости вдоль твердой стенки происходит торможение потока, обусловленное вязкостью (рис. 1.3). Скорость v уменьшается по мере уменьшения расстояния у от стенки вплоть до v = 0 при у = 0, а между сдоями происходит проскальзывание, сопровождающееся возникновением касательных напряжений (напряжений трения), Согласно гипотезе, высказанной впервые Ньютоном в 1686 г., а затем экспериментально обоснованной проф. Н. П. Петровым в 1883 г., касательное напряжение в жидкости зависит от ее рода и характера течения и при слоистом течении изменяется прямо пропорционально так называемому поперечному градиенту скорости. Таким образом 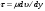 (1.18) (1.18)где μ — коэффициент пропорциональности, получивший название динамической вязкости жидкости; dv — приращение скорости, соответствующее приращению координаты dy (см. рис. 1.3). Поперечный градиент скорости dv/dyопределяет изменение скорости, приходящееся на единицу длины в направлении нормали к стенке и, следовательно, характеризует интенсивность сдвига жидкости в данной точке (точнее dv/dy — это модуль градиента скорости; сам градиент — вектор). Из закона трения (5.11), следует, что напряжения трения возможны только в движущейся жидкости, т. е. вязкость жидкости проявляется лишь при ее течении. В покоящейся жидкости касательные напряжения будем считать равными нулю *. Изложенное позволяет сделать вывод, что трение в жидкостях, обусловленное вязкостью, подчинено закону, принципиально отличному от закона трения твердых тел. Если течение жидкости таково, что имеется еще градиент скорости в направлении, нормальном к плоскости рисунка (см. рис. 1.2), то полную производную в формуле (5.11) надо заменить частной производной dv/dy. При постоянстве касательного напряжения по поверхности Sполная касательная сила (сила трения), действующая по этой поверхности 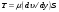 (1.19) (1.19)Для определения размерности вязкости μ (Па*с) решим уравнение (5.11) относительно μ, в результате чего получим 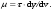 Наряду с динамической вязкостью μ применяют кинематическую: 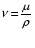 (1.20) (1.20)Единицей измерения кинематической вязкости является стокc: 1 Ст = 1 см2/с. Сотая доля стокса называется сантистоксом (сСт). Вязкость капельных жидкостей зависит от температуры и уменьшается с увеличением последней (рис. 1.3). Вязкость газов, наоборот, с увеличением температуры возрастает. Объясняется это различием природы вязкости в жидкостях и газах. В жидкостях молекулы расположены гораздо ближе друг к другу, чем в газах, и вязкость вызывается силами молекулярного сцепления. Эти силы с увеличением температуры уменьшаются, поэтому вязкость падает, В газах же вязкость обусловлена, главным образом, беспорядочным тепловым движением молекул, интенсивность которого увеличивается с повышением температуры. Поэтому вязкость газов с увеличением температуры возрастает. Влияние температуры на вязкость жидкостей можно оценить формулой 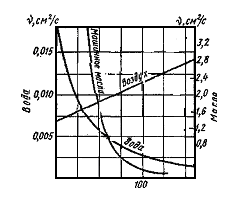 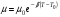 (1.21) (1.21)где μ и μ0 — вязкости при температуре Т и Т0; β — коэффициент, значение которого для масел изменяется в пределах 0,02—0,03. Рис. 1.4 Зависимость относительной вязкости μ/μ0 от давления для предельных значений коэффициента α. Вязкость жидкостей зависит также от давления, однако эта зависимость существенно проявляется лишь при относительно больших изменениях давления (в несколько десятков МПа). С увеличением давления вязкость большинства жидкостей растает, что может быть оценено формулой 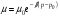 где μ и μ0 — вязкости при давлении р и р0, 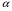 - коэффициент, значение которого для минеральных масел изменяется в пределах 0,02-0,03 (нижний предел соответствует высоким температурам, а верхний - низким). - коэффициент, значение которого для минеральных масел изменяется в пределах 0,02-0,03 (нижний предел соответствует высоким температурам, а верхний - низким). Приближенная зависимость относительной вязкости μ/μ0 от давления для минеральных масел показана на (рис. 1.4) для предельных значений коэффициента α. Вязкость жидкостей измеряют при помощи, вискозиметров. Наиболее распространенным является вискозиметр Энглера, который представляет собой цилиндрический сосуд диаметром 106 мм, с короткой трубкой диаметром 2,8 мм, встроенной в дно. Время t истечения 200 см3 испытуемой жидкости из вискозиметра через эту трубку под действием силы тяжести, деленное на время tвод истечения того же объема дистиллированной воды при 20° С выражает вязкость в градусах Энглера: 1 °Е = t/tвод, где tвод = 51,6 с. Для пересчета градусов Энглера в стоксы в случае минеральных масел применяют формулу 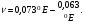 Ж). Испаряемость свойственна всем капельным жидкостям, однако интенсивность испарения неодинакова у различных жидкостей и зависит от условий, в которых они находятся. Одним из показателей, характеризующих испаряемость жидкости, является температура ее кипения при нормальном атмосферном давлении; чем выше температура кипения, тем меньше испаряемость жидкости. В гидросистемах нормальное атмосферное давление является лишь частным случаем; обычно приходится иметь дело с испарением, а иногда и кипением жидкостей в замкнутых объемах при различных температурах и давлениях. Поэтому более полной характеристикой испаряемости является давление (упругость) насыщенных паров рн п, выраженное в функции температуры. Чем больше давление насыщенных паров при данной температуре, тем больше испаряемость жидкости. С увеличением температуры давление рн.пувеличивается, однако у разных жидкостей в разной степени. Если для простой жидкости рассматриваемая зависимость является вполне определенной, то для сложных жидкостей, представляющих собой многокомпонентные смеси (например, для бензина и др.), давление />н.п зависит не только от физико-химических свойств и температуры, но и от соотношения объемов жидкой и паровой фаз, Давление насыщенных паров возрастает с увеличением части объема, занятого жидкой фазой. Обычно значения упругости паров сложных жидкостей даются для отношения паровой и жидкой фаз, равного 4:1. З). Растворимость газов в жидкостях характеризуется количеством растворенного газа в единице объема жидкости, различна для разных жидкостей и изменяется с увеличением давления. Относительный объем газа, растворенного в жидкости до ее полного насыщения, можно считать по закону Генри прямо пропорциональным давлению, т. е. 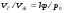 , ,где VГ — объем растворенного газа, приведенный к нормальным условиям (p0, T0); VЖ — объем жидкости; k — коэффициент растворимости; р — давление жидкости. Коэффициент kимеет следующие значения при 20 °С: для воды 0,016, керосина 0,13, минеральных масел 0,08, жидкости АМГ-10 — 0,1. При понижении давления выделяется растворенный в жидкости газ, причем интенсивнее, чем растворяется в ней. Это явление может отрицательно сказываться на работе гидросистем.
Гидростатическое давление и его свойство Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практические приложения. Как следует из гл. 1, жидкости практически не способны сопротивляться растяжению, а в неподвижных жидкостях не действуют касательные силы. Поэтому на неподвижную жидкость из поверхностных сил могут действовать только силы давления; причем на внешней поверхности рассматриваемого объема жидкости силы давления всегда направлены по нормали внутрь объема жидкости и, следовательно, являются сжимающими. Под внешней поверхностью жидкости понимают не только поверхность раздела жидкости с газообразной средой или твердыми стенками, но и поверхность объема, мысленно выделяемого из общего объема жидкости. Таким образом, в неподвижной жидкости возможен лишь один вид напряжения напряжение сжатия, т. е. гидростатическое давление. Рассмотрим основное свойство гидростатического давления: в любой точке жидкости гидростатическое давление не зависит от ориентировки площадки, на которую оно действует, т. е. от углов ее наклона по отношению к координатным осям. Для доказательства этого свойства выделим в неподвижной жидкости элементарный объем в форме тетраэдра с ребрами, параллельными координатным осям и соответственно равными 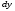 и и 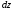 (рис.2.1). Пусть внутри выделенного объема на жидкость действует единичная массовая сила, составляющие которой равны (рис.2.1). Пусть внутри выделенного объема на жидкость действует единичная массовая сила, составляющие которой равны 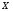 , , 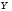 и и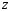 . Обозначим через . Обозначим через 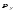 — давление на грань, нормальную к оси — давление на грань, нормальную к оси , и т. д. Гидростатическое давление, действующее на наклонную грань, обозначим через , и т. д. Гидростатическое давление, действующее на наклонную грань, обозначим черезСоставим уравнение равновесия выделенного объема жидкости сначала в направлении оси 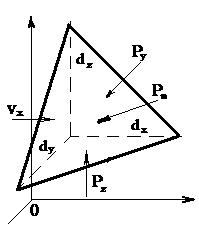 Рис. 1.4 Элементарный объем в форме тетраэдра с ребрами, параллельными координатным осям и соответственно равными 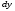 и и 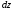 Проекция сил давления на ось Масса жидкости в тетраэдре равна произведению ее объема на плотность, т. е. 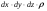 , следовательно, массовая сила, действующая на тетраэдр вдоль оси , следовательно, массовая сила, действующая на тетраэдр вдоль оси 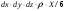 . .Уравнение равновесия тетраэдра запишем в виде: 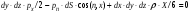 . .Разделив это уравнение на площадь 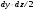 , которая равна площади проекции наклонной грани , которая равна площади проекции наклонной грани 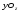 , т. е. , т. е. 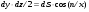 , получим , получим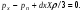 При стремлении размеров тетраэдра к нулю последний член уравнения, содержащий множитель Аналогично составляя уравнения равновесия вдоль осей 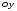 и и 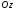 , находим , находим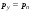 , , 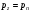 или или 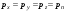 (2.1) (2.1)Так как размеры тетраэдра 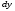 и и 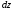 взяты произвольно, то и наклон площадки взяты произвольно, то и наклон площадки 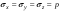 . .Рассмотренное свойство давления в неподвижной жидкости имеет место также при движении невязкой жидкости. При движении же реальной жидкости возникают касательные напряжения, вследствие чего давление в реальной жидкости указанным свойством, строго говоря, не обладает. Основное уравнение гидростатики Рассмотрим распространенный частный случай равновесия жидкости, когда на нее действует лишь одна массовая сила, сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объема жидкости. Если этот объем весьма мал по сравнению с объемом Земли, то свободную поверхность жидкости можно считать горизонтальной плоскостью. Пусть жидкость содержится в сосуде и на ее свободную поверхность действует давление 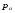 . Найдем гидростатическое давление . Найдем гидростатическое давление 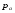 в произвольно взятой точке М, расположенной на глубине в произвольно взятой точке М, расположенной на глубине 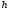 . .Выделим около точки М элементарную горизонтальную площадку dSи построим на ней вертикальный цилиндрический объем высотой 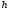 . Рассмотрим условие равновесия указанного объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь будет внешним и направлено по нормали внутрь объема, т. е. вверх. . Рассмотрим условие равновесия указанного объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь будет внешним и направлено по нормали внутрь объема, т. е. вверх.Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикаль:  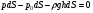 . .Последний член уравнения представляет собой вес жидкости в указанном объеме. Силы давления по боковой поверхности цилиндра в уравнение не входят, так как они нормальны к вертикали. Сократив ,выражение на 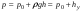 (2.2) (2.2)Полученное уравнение называют основным уравнением. гидростатики; по нему можно подсчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления 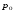 на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости. на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.Величина 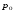 является одинаковой для всех точек объема жидкости, поэтому, учитывая свойство гидростатического давления, можно сказать, что давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости и по всем направлениям одинаково. Это положение известно под названием закона Паскаля. является одинаковой для всех точек объема жидкости, поэтому, учитывая свойство гидростатического давления, можно сказать, что давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости и по всем направлениям одинаково. Это положение известно под названием закона Паскаля.Давление жидкости, как видно из формулы (2.2), возрастает с увеличением глубины по закону прямой и на данной глубине есть величина постоянная. Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня. В данном случае поверхностями уровня являются горизонтальные плоскости, а свободная поверхность является одной из поверхностей уровня. Возьмем на произвольной высоте горизонтальную плоскость сравнения, от которой вертикально вверх будем отсчитывать координаты 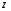 . Обозначив через . Обозначив через 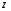 координату точки М, через координату точки М, через 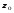 координату свободной поверхности жидкости и заменив в уравнении (2.2) hна координату свободной поверхности жидкости и заменив в уравнении (2.2) hна 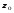 и и 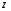 , получим , получим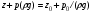 . (2.3) . (2.3)Так как точка М взята произвольно, можно утверждать, что для всего рассматриваемого неподвижного объема жидкости  . .Координата 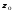 называется геометрической высотой. Величина называется геометрической высотой. Величина 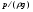 имеет линейную размерность и называется пьезометрической высотой. Сумма имеет линейную размерность и называется пьезометрической высотой. Сумма 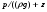 ) называется гидростатическим напором. ) называется гидростатическим напором.Таким образом, гидростатический напор есть величина постоянная для всего объема неподвижной жидкости. Те же результаты можно получить путем интегрирования дифференциальных уравнений равновесия жидкости, которые рассмотрены в следующем параграфе. Дифференциальные уравнения равновесия жидкости и их интегрирование для простейшего случая Получим дифференциальные уравнения равновесия жидкости в общем случае, когда на нее действуют не только сила тяжести, но и другие массовые силы, например, силы инерции переносного движения при так называемом относительном покое. В неподвижной жидкости возьмем произвольную точку М с координатами 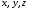 и давлением р. Систему координат будем считать жестко связанной с сосудом, содержащим жидкость. Выделим в жидкости элементарный объем в форме прямоугольного параллелепипеда с ребрами, параллельными координатным осям и соответственно равными и давлением р. Систему координат будем считать жестко связанной с сосудом, содержащим жидкость. Выделим в жидкости элементарный объем в форме прямоугольного параллелепипеда с ребрами, параллельными координатным осям и соответственно равными 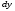 и и 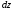 . Пусть точка М будет одной из вершин параллелепипеда. Рассмотрим условия равновесия выделенного объема жидкости. Пусть внутри параллелепипеда на жидкость действует равнодействующая массовая сила, составляющие которой, отнесенные к единице массы , равны . Пусть точка М будет одной из вершин параллелепипеда. Рассмотрим условия равновесия выделенного объема жидкости. Пусть внутри параллелепипеда на жидкость действует равнодействующая массовая сила, составляющие которой, отнесенные к единице массы , равны Давление 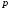 есть функция координат есть функция координат 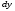 и и 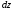 ., но вблизи точки М по всем трем граням параллелепипеда оно одинаково, что вытекает из доказанного выше свойства гидростатического давления .При переходе от точки М, например, к точке N изменяется лишь координата ., но вблизи точки М по всем трем граням параллелепипеда оно одинаково, что вытекает из доказанного выше свойства гидростатического давления .При переходе от точки М, например, к точке N изменяется лишь координата  на бесконечно малую величину на бесконечно малую величину 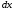 , в связи с чем функция , в связи с чем функция 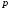 получает приращение, равное частному дифференциалу получает приращение, равное частному дифференциалу 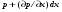 , ,где 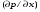 — градиент давления вблизи точки М в направлении оси — градиент давления вблизи точки М в направлении оси  . .Рассматривая давления в других соответствующих точках граней, нормальных к оси  видим, что они отличаются на одинаковую (с точностью до бесконечно малых высших порядков) величину. видим, что они отличаются на одинаковую (с точностью до бесконечно малых высших порядков) величину. Ввиду этого разность сил давления, действующих на параллелепипед в направлении оси  , равна указанной величине, умноженной , равна указанной величине, умноженнойна площадь грани:  . .Аналогичным образом, но через градиенты давления 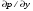 и и На выделенный параллелепипед действуют лишь указанные массовые силы и силы давления, поэтому уравнения равновесия параллелепипеда в направлениях трех координатных осей запишем в следующем виде: Разделим эти уравнения на массу 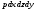 параллелепипеда и перейдем к пределу, устремляя параллелепипеда и перейдем к пределу, устремляя 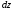 ., к нулю, т. е. стягивая параллелепипед к исходной точке М. Тогда в пределе получим уравнения равновесия жидкости, отнесенные к точке М: ., к нулю, т. е. стягивая параллелепипед к исходной точке М. Тогда в пределе получим уравнения равновесия жидкости, отнесенные к точке М: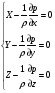 (2.5) (2.5)Система (2.5) дифференциальных уравнений гидростатики называется уравнениями Эйлера . Для практического пользования удобнее вместо системы уравнений (2.5) получить одно эквивалентное им уравнение, не содержащее частных производных. Для этого умножим первое из уравнений (2.5) на 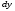 , третье на , третье на 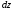 и, сложив все три уравнения, получим и, сложив все три уравнения, получимТрехчлен, заключенный в скобках, представляет собой полный дифференциал давления, т. е. функции 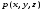 , поэтому предыдущее уравнение можно переписать в виде: , поэтому предыдущее уравнение можно переписать в виде:или, 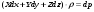 (2.6) (2.6)Полученное уравнение выражает приращение давления dpпри изменении координат на 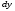 и и 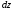 ., вобщем случае равновесия жидкости. ., вобщем случае равновесия жидкости.Если предположить, что на жидкость действует только сила тяжести, и направить ось zвертикально вверх, то X=Y=O, Z=gи, следовательно, вместо уравнения (2.7) для этого частного случая равновесия жидкости получим  (2.7) (2.7)После интегрирования будем иметь 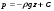 Постоянную интегрирования найдем, подставив параметры свободной поверхности, для которой при z = z0 p= р0 Получим 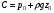 . .При этом 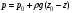 (2.8) (2.8)или 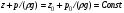 Заменяя в уравнении(2.8) разность 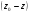 на h глубину расположения точки М, найдем на h глубину расположения точки М, найдем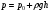 . .Получили то же основное уравнение гидростатики ,которое было выведено в предыдущем параграфе иным путем. Пьезометрическая высота. Вакуум. Измерение давления В данном параграфе, продолжим рассмотрение важнейшего частного случая равновесия жидкости, равновесие в поле лишь одной массовой силы, силы тяжести. Рис. 1.5 Пьезометр Пьезометрическая высота, равная 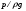 , представляет собой высоту столба данной жидкости, соответствующую данному давлению , представляет собой высоту столба данной жидкости, соответствующую данному давлению 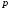 (абсолютному или избыточному). Пьезометрическую высоту, соответствующую избыточному давлению, можно определить по пьезометру простейшему устройству для измерения давления. Пьезометр представляет собой вертикальную стеклянную трубку, верхний конец которой открыт в атмосферу, а нижний присоединен к емкости, в которой измеряется давление (рис. 1.5). (абсолютному или избыточному). Пьезометрическую высоту, соответствующую избыточному давлению, можно определить по пьезометру простейшему устройству для измерения давления. Пьезометр представляет собой вертикальную стеклянную трубку, верхний конец которой открыт в атмосферу, а нижний присоединен к емкости, в которой измеряется давление (рис. 1.5).Применяя формулу к жидкости, заключенной в пьезометре, получим 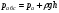 . .где 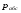 — абсолютное давление в жидкости на уровне присоединения пьезометра; — абсолютное давление в жидкости на уровне присоединения пьезометра; 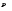 — атмосферное давление. — атмосферное давление.Отсюда высота подъема жидкости в пьезометре 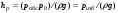 ), (2.9) ), (2.9)где ризб — избыточное давление на уровне присоединения пьезометра. Очевидно, что если на свободную поверхность покоящейся жидкости действует атмосферное давление, то пьезометрическая высота для любой точки рассматриваемого объема жидкости равна глубине расположения этой точки. Часто Давление в жидкостях или газах численно выражают в виде соответствующей этому давлению пьезометрической высоты по формуле (2.9). Если абсолютное давление в жидкости или газе меньше атмосферного, то говорят, что имеет место разрежение, или вакуум. За величину разрежения, или вакуума, принимается недостаток до атмосферного давления: 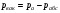 или или 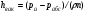 Простейшим устройством для измерения вакуума может служить стеклянная трубка, показанная на рис. 1.6 в двух вариантах. Вакуум в жидкости А можно измерять при помощи U-образной трубки (см. рисунок справа) или перевернутой U-образной трубки, один конец которой опущен в сосуд с жидкостью (см. рисунок слева). Для измерения давления жидкостей и газов в лабораторных условиях помимо пьезометра пользуются жидкостными и механическими манометрами. Так называемый U-образный манометр представляет собой изогнутую стеклянную трубку, содержащую ртуть. При измерении небольших давлений газа вместо ртути применяют спирт, воду и иногда тетрабром метан (δ = 2,95). Если измеряется давление жидкости в точке М, и соединительная трубка заполнена этой же жидкостью, то следует учитывать высоту расположения манометра над точкой М. Так, избыточное давление в точке М 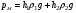 Чашечный манометр удобнее описанного выше тем, что при пользовании им необходимо фиксировать положение лишь одного уровня жидкости (при достаточно большом диаметре чашки по сравнению с диаметром трубки уровень жидкости в чашке можно считать неизменным). Для измерения разности давлений в двух точках служат дифференциальные манометры, простейшим из которых является U-образный манометр. Если при помощи такого манометра, обычно заполняемого ртутью, измерена разность давлений  и и 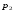 в жидкости плотностью в жидкости плотностью 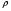 , которая полностью заполняет соединительные трубки, то , которая полностью заполняет соединительные трубки, то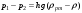 . .Для измерения малых перепадов давления воды применяют двух-жидкостный микроманометр, представляющий собой перевернутую U-образную трубку с маслом или керосином в верхней части. Для этого случая 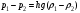 Для измерения давлений более 0,2 — 0,3 МПа применяют механические манометры — пружинные или мембранные. Принцип их действия основан на деформации полой пружины или мембраны под действием измеряемого давления. Через механизм эта деформация передается стрелке, которая показывает величину измеряемого давления на циферблате. Наряду с механическими манометрами применяют электрические манометры. В качестве чувствительного элемента (датчика) в электроманометре используют мембрану. Под действием измеряемого давления мембрана деформируется и через передаточный механизм перемещает движок потенциометра, который вместе с указателем включен в электрическую схему. Сила давления жидкости на плоскую стенку Используем основное уравнение гидростатики (1.20) для нахождения полной силы давления жидкости на плоскую стенку, наклоненную к горизонту под произвольным углом а (рис. 1.7). Вычислим силу Fдавления, действующую со стороны жидкости на некоторый участок рассматриваемой стенки, ограниченный произвольным контуром и имеющий площадь, равную S. Ось 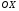 направим по линии пересечения плоскости стенки со свободной поверхностью жидкости, а ось направим по линии пересечения плоскости стенки со свободной поверхностью жидкости, а ось 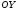 — перпендикулярно к этой линии в плоскости стенки. — перпендикулярно к этой линии в плоскости стенки.Выразим сначала элементарную силу давления, приложенную к бесконечно малой площадке 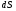 : :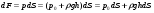 где 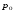 — давление на свободной поверхности; — давление на свободной поверхности; 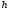 — глубина расположения площадки — глубина расположения площадки 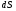 . .Для определения полной силы 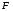 проинтегрируем полученное выражение по всей площади проинтегрируем полученное выражение по всей площади 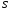 : :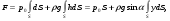 где 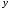 — координата площадки — координата площадки 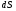 . .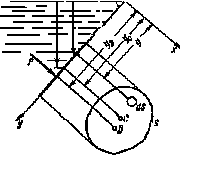 Рис. 1.7 Последний интеграл представляет собой статический момент площади 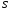 относительно оси относительно оси 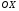 и равен произведению этой площади на координату ее центра тяжести и равен произведению этой площади на координату ее центра тяжести(точка С), т. е. 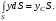 Следовательно, 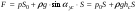 (здесь 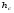 — глубина расположения центра тяжести площади S.), — глубина расположения центра тяжести площади S.),или 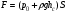 (1.29) (1.29)т. е. полная сила давления жидкости на плоскую стенку равна произведению площади стенки на гидростатическое давление 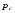 в центре тяжести этойплощади. в центре тяжести этойплощади.В частном случае, когда давление Ро 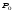 является атмосферным и действует также с другой стороны стенки, сила является атмосферным и действует также с другой стороны стенки, сила 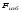 избыточного давления жидкости на плоскую стенку равна лишь силе избыточного давления жидкости на плоскую стенку равна лишь силе 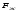 давления от веса жидкости, т. е. давления от веса жидкости, т. е.Fизб=F В общем случае давление 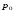 может существенно отличаться от атмосферного, поэтому полную силу может существенно отличаться от атмосферного, поэтому полную силу 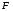 давления жидкости на стенку будем рассматривать как сумму двух сил: давления жидкости на стенку будем рассматривать как сумму двух сил: 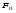 от внешнего давления от внешнего давления 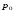 исилы исилы 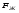 от веса жидкости, т.е. от веса жидкости, т.е.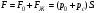 Рассмотрим вопрос о точках приложения этих сил, называемых центрами давления. Так как внешнее давление 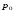 передается всем точкам площади передается всем точкам площади 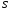 одинаково, то его равнодействующая одинаково, то его равнодействующая 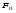 будет приложена в центре тяжести площади будет приложена в центре тяжести площади 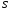 . Для нахождения точки приложения силы давления . Для нахождения точки приложения силы давления 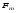 от веса жидкости (точка D) применим теорему механики, согласно которой момент равнодействующей силы относительно оси от веса жидкости (точка D) применим теорему механики, согласно которой момент равнодействующей силы относительно оси 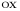 равен сумме моментов составляющих сил, т. е. равен сумме моментов составляющих сил, т. е.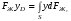 где 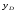 — координата точки приложения силы — координата точки приложения силы 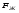 . Выражая . Выражая 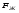 и и 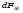 через через 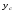 и и 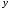 и определяя и определяя 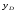 , получаем , получаем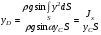 где 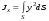 Jx— момент инерции площади Jx— момент инерции площади 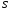 относительно оси относительно оси 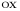 . .Учитывая, что 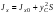 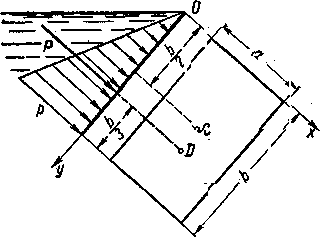 Рис. 1.8 Эпюра давления- жидкости на прямоугольную стенку (Jx0 — момент инерции площади 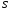 относительно центральной оси, параллельной относительно центральной оси, параллельной 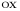 ), находим ), находим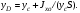 (1.30) (1.30)Таким образом, точка приложения силы 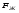 расположена ниже центра тяжести площади стенки; расстояние между ними расположена ниже центра тяжести площади стенки; расстояние между нимиЕсли давление 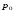 равно атмосферному, то точка Dи будет центром давления. При равно атмосферному, то точка Dи будет центром давления. При 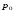 выше атмосферного центр давления находят по правилам механики как точку приложения равнодействующей двух сил: F0и выше атмосферного центр давления находят по правилам механики как точку приложения равнодействующей двух сил: F0и 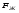 ; чем больше первая сила по сравнению со второй, тем, очевидно, центр давления ближе к центру тяжести площади S. ; чем больше первая сила по сравнению со второй, тем, очевидно, центр давления ближе к центру тяжести площади S.В частном случае, когда стенка имеет форму прямоугольника размерами, а х b(рис. 1.14) и одна из его сторон, а лежит на свободной поверхности с атмосферным давлением, центр давления Dнаходится на расстоянии b/3 от нижней стороны. Сила давления жидкости на криволинейные стенки. Плавание тел Нахождение силы давления жидкости на поверхности произвольной формы в общем случае приводится к определению трех составляющих суммарной силы и трех моментов. Чаще всего рассматривают цилиндрические или сферические поверхности, имеющие вертикальную плоскость симметрии. Сила давления жидкости в этом случае сводится к равнодействующей силе, лежащей в плоскости симметрии. Возьмем цилиндрическую поверхность АВ с образующей, перпендикулярной к плоскости чертежа (рис. 1.9), и определим силу давления жидкости на эту поверхность в двух случаях: 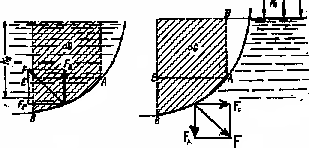 Рис1.9,а Рис1.9,б (Рис. 1.9) Схема для определения силы давления жидкости на цилиндрическую поверхность 1) жидкость расположена сверху (рис. 1.9, а); 2) жидкость расположена снизу (рис. 1.9, б). В первом случае выделим объем жидкости, ограниченный рассматриваемой поверхностью АВ, вертикальными поверхностями, проведенными через границы этого участка, и свободной поверхностью жидкости, т. е. объем ABCD, и рассмотрим условия его равновесия в вертикальном и горизонтальном направлениях. Если жидкость действует на стенку АВ с силой 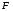 , то стенка АВ действует на жидкость с силой , то стенка АВ действует на жидкость с силой 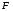 , направленной в обратную сторону. На рис. 1.15 показана эта сила реакции, разложенная на две составляющие: горизонтальную , направленной в обратную сторону. На рис. 1.15 показана эта сила реакции, разложенная на две составляющие: горизонтальную 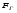 и вертикальную и вертикальную 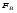 . .Условие равновесия объема ABCD в вертикальном направлении имеет вид FB = p0SГ + G, (1.31) где 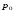 — давление на свободной поверхности жидкости; SГ — площадь горизонтальной проекции поверхности АВ; G — вес выделенного объема жидкости. — давление на свободной поверхности жидкости; SГ — площадь горизонтальной проекции поверхности АВ; G — вес выделенного объема жидкости.Условие равновесия того же объема в горизонтальном направлении запишем с учетом того, что силы давления жидкости на поверхности ЕС и ADвзаимно уравновешиваются и остается лишь сила давления на площадь BE, т. е. на вертикальную проекцию поверхности АВ — SB. Тогда  FГ=SBρghC+p0SB (1.32) FГ=SBρghC+p0SB (1.32)Определив по формулам (1.31) и (1.32) вертикальную и горизонтальную составляющие полной силы давления 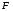 F, найдем F, найдем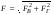 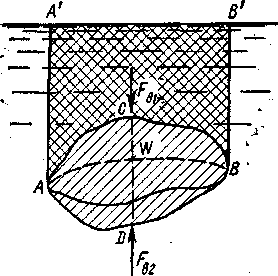 Рис 1.10. Схема для подтверждения закона Архимеда. Когда жидкость расположена снизу (см. рис. 1.9, б), гидростатическое давление во всех точках поверхности АВ имеет те же значения, что и в первом случае, но направление его будет противоположным, и суммарные силы FBи Frопределятся теми же формулами (1.31) и (1.32), но с обратным знаком. При этом под величиной Gследует понимать так же, как и в первом случае, вес жидкости в объеме ABCD, хотя этот объем и не заполнен жидкостью. Положение центра давления на цилиндрической стенке можно легко найти, если известны силы FB ж Frnопределены центр давления на вертикальной проекции стенки и центр тяжести выделенного объема ABCD. Задача значительно облегчается в том случае, когда рассматриваемая цилиндрическая поверхность является круговой. Равнодействующая сила при этом пересекает ось поверхности, так как любая элементарная сила давления нормальна к поверхности, т. е. направлена по радиусу. Изложенный способ определения силы давления на цилиндрические поверхности применим и к сферическим поверхностям, причем равнодействующая сила в этом случае также проходит через центр поверхности и лежит в вертикальной плоскости симметрии. Описанный выше прием нахождения, вертикальной составляющей силы давления жидкости на криволинейную стенку используют для доказательства закона Архимеда. Пусть в жидкость погружено тело произвольной формы объемом V(рис. 1.16). Спроектируем его на свободную поверхность жидкости и проведем проектирующую цилиндрическую поверхность, которая касается поверхности тела по замкнутой кривой. Эта кривая отделяет верхнюю часть поверхности тела АСВ от нижней ее части ADB. Вертикальная составляющая Fsiсилы избыточного давления жидкости на верхнюю часть поверхности тела направлена вниз и равна весу жидкости в объеме АА'В'ВСА. Вертикальная составляющая FBa силы давления жидкости на нижнюю часть поверхности тела направлена вверх и равна весу жидкости в объеме AA'B'BDA. Отсюда следует, что вертикальная равнодействующая сил давления жидкости на тело будет направлена вверх и равна весу жидкости в объеме, равном разности указанных двух объемов, т. е. FA=FB2-FB1=GACBD=Vρg В этом и заключается закон Архимеда, обычно формулируемый так: на тело, погруженное в жидкость, действует выталкивающая сила, направленная вертикально вверх, численно равная весу жидкости, вытесненной телом, и приложенная в центре тяжести объема погруженной части тела. Сила faназывается архимедовой силой, или силой поддержания, а точка ее приложения, т. е. центр тяжести объема F, — центром водоизмещения. В зависимости от соотношения веса Gтела и архимедовой силы faвозможны три случая: 1) G> fa— тело тонет; 2) G< fa— тело всплывает и плавает на поверхности жидкости в частично погруженном состоянии; 3) G= fa— тело плавает в полностью погруженном состоянии. Для равновесия плавающего тела кроме равенства сил G = faдолжен быть равен нулю суммарный момент. Последнее условие соблюдается тогда, когда центр тяжести тела лежит на одной вертикали с центром водоизмещения. Условие устойчивого равновесия тела, плавающего в полностью погруженном состоянии, заключается в следующем: центр тяжести тела должен находиться ниже центра водоизмещения. Устойчивость равновесия тел, плавающих на поверхности жидкости, здесь не рассматривается. |
