Лекции. 1. Введение. 1 Предмет гидравлики и краткая история её развития
 Скачать 1.38 Mb. Скачать 1.38 Mb.
|
                                                    Содержание Содержание1. Введение. 1.1 Предмет гидравлики и краткая история её развития. 1.2 Гидростатика 1.3 Кинематика 1.4 Общие уравнения сплошной среды 1.5 Потери напора при установившемся движении. 2. Объемные гидромашины. 2.1 Понятие объемной гидромашины. Насосы, гидродвигатели. 2.2 Величины характеризующие рабочий процесс ОГМ. 2.3 Роторные гидромашины. Классификация. 3. Основные сведения об оъемном гидроприводе. 3.1 Назначения и основные свойства 3.2 Основные параметры гидрооборудования. 3.3 Основные режимы работы и условия эксплуатации гидрооборудования. 1. Введение
Раздел механики, в котором изучают равновесие и движение жидкости, а также силовое взаимодействие жидкостью и обтекаемыми ею телами или ограничивающими её поверхностями, называется гидромеханикой. Науку о законах равновесия и движения жидкостей и о способах приложения этих законов к решению практических задач называют гидравликой. В гидравлике рассматривают, главным образом, потоки жидкости, ограниченные и направленные твердыми стенками, т. е. течение в закрытых и открытых каналах. Таким образом, можно сказать, что в гидравлике изучают в основном внутренние течения жидкостей и решают так называемую внутреннюю задачу в отличие от внешней, связанной с внешним обтеканием тел сплошной средой, которое имеет место при движении тела в жидкости или газе. Историческое развитие механики жидкостей шло двумя различными путями: -первый путь – теоретический, путь точного математического анализа, основанного на законах механики. Он привел к созданию теоретической гидромеханики, которая долгое время являлась самостоятельной дисциплиной, непосредственно не связанная с экспериментом. Однако на пути чистого теоретического исследования движения жидкости встречается множество трудностей, и методы теоретической гидромеханики не всегда дают ответы на вопросы, выдвигаемые практикой. - второй путь – путь широкого применения эксперимента и накопления опытных данных для использования их в инженерной практике – привел к созданию гидравлики. Понятие жидкости. Реальная и идеальная жидкости Жидкость– физическое тело, молекулы которого слабо связаны между содой. Поэтому незначительные силы способны легко изменить форму жидкости, которая способна сохранить объем, но не форму. В гидравлике жидкость рассматривают как непрерывную среду, заполняющую пространство без пустот и промежутков, т.е. отвлекаются от молекулярного строения жидкости и её частицы, даже бесконечно малые, считают состоящими из большого числа молекул. Реальной жидкостью называют жидкость, обладающую вязкостью (свойство жидкости сопротивляться сдвигу ее слоев). Идеальная или невязкая жидкость является упрощенной моделью реальной (вязкой) жидкости. По предположению, идеальная жидкость имеет все свойства реальной, кроме вязкости. 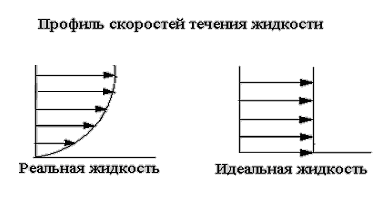 рис. 1.1 Профиль скоростей течения жидкости. Метод гидравлических исследований Метод, используемый в современной гидравлике, заключается в следующем: исследуемые явления сначала упрощают и к ним применяют законы теоретической механики. Затем полученные результаты сравнивают с данными опытов, выясняют степень расхождения, уточняют и исправляют теоретические выводы и формулы для приспособления их к практическому использованию. Гидравлика дает методы расчета и проектирования разнообразных гидротехнических сооружений (плотин, каналов, водосливов, трубопроводов для подачи всевозможных жидкостей), гидромашин (насосов, гидротурбин, гидропередач), а также других гидравлических устройств, применяемых во многих областях техники. Особенно велико значение гидравлики в машиностроении, где приходится иметь дело с закрытыми руслами (например, трубами) и напорными течениями в них, т. е. с потоками без свободной поверхности и с давлением, отличным от атмосферного. Гидросистемы, состоящие из насосов, трубопроводов, различных гидроагрегатов широко используют в машиностроении в качестве систем жидкостного охлаждения, топливоподачи, смазочных и др. На различных современных машинах все более широкое применение находят гидропередачи (гидроприводы) и гидроавтоматика. Гидропередачи представляют собой устройства для передачи механической энергии и преобразования движения посредством жидкости. По сравнению с передачами других видов (зубчатыми и т. п.) гидропередачи имеют ряд существенных преимуществ: простота преобразования вращательного движения в возвратно-поступательное, возможность плавного (бесступенчатого) изменения соотношения скоростей входного и выходного звеньев, компактность конструкций и малая масса гидромашин при заданной мощности по сравнению, например, с электромашинами и др. Гидропередачи, снабженные системами автоматического или ручного управления, образуют гидроприводы, которые благодаря перечисленным преимуществам широко используют в различных металлообрабатывающих станках, на летательных аппаратах (самолетах, вертолетах, ракетах), на сухопутных транспортных машинах (колесных и гусеничных), в строительно-дорожных и подъемно-транспортных машинах, в прокатных станах и прессах и т. п. Гидроприводы, гидроавтоматика и различные гидравлические устройства являются весьма перспективными для комплексной автоматизации и механизации производства. Для расчета и проектирования гидроприводов, их систем автоматического регулирования и других устройств с гидромашинами и гидроавтоматикой, а также для правильной их эксплуатации, ремонта и наладки нужно иметь соответствующую подготовку в области гидравлики и теории гидромашин. Силы, действующие на жидкость. Понятие давления Жидкость в гидравлике рассматривают как непрерывную среду, заполняющую пространство без пустот и промежутков, т. е. отвлекаются от молекулярного строения жидкости и ее частицы, даже бесконечно малые, считают состоящими из большого числа молекул. Вследствие текучести (подвижности частиц) в жидкости действуют силы не сосредоточенные, а непрерывно распределенные по ее объему (массе) или поверхности. В связи с этим силы, действующие на объемы жидкости и являющиеся по отношению к ним внешними, разделяют на массовые (объемные) и поверхностные. Массовые силы в соответствии со вторым законом Ньютона пропорциональны массе жидкости или, для однородной жидкости, — ее объему. К ним относятся сила тяжести и сила инерции переносного движения, действующая на жидкость при относительном ее покое в ускоренно движущихся сосудах или при относительном движении жидкости в руслах, перемещающихся с ускорением. Поверхностные силы непрерывно распределены по поверхности жидкости и при равномерном их распределении пропорциональны площади этой поверхности. Эти силы обусловлены непосредственным воздействием соседних объемов жидкости на данный объем или же воздействием других тел (твердых или газообразных), соприкасающихся с данной жидкостью. Как следует из третьего закона Ньютона, с такими же силами, но в противоположном направлении, жидкость действует на соседние с нею тела. В общем случае поверхностная сила 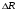 , действующая на площадке , действующая на площадке 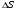 , направлена под некоторым углом к ней, и ее можно разложить на нормальную , направлена под некоторым углом к ней, и ее можно разложить на нормальную 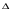 Fи тангенциальную Fи тангенциальную  Tсоставляющие (рис. 1.2). Первая называется силой давления, а вторая — силой трения. Tсоставляющие (рис. 1.2). Первая называется силой давления, а вторая — силой трения.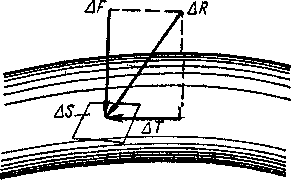 Рис. 1.2 Силы, действующие на жидкость. Как массовые, так и поверхностные силы в гидромеханике рассматривают обычно в виде единичных сил, т. е. сил, отнесенных к соответствующим единицам. Массовые силы относят к единице массы, а поверхностные к единице площади Так как массовая сила равна произведению массы на ускорение, следовательно, единичная массовая сила численно равна соответствующему ускорению. Единичная поверхностная сила, называемая напряжением поверхностной силы, раскладывается на нормальное и касательное напряжения. Нормальное напряжение, т.е. напряжение силы давления, называется гидромеханическим,в случае покоя - гидростатическим давлением,или просто давлением, и обозначается буквой  Если сила давления 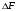 равномерно распределена по площадке равномерно распределена по площадке 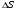 , то среднее гидромеханическое давление определяют по формуле , то среднее гидромеханическое давление определяют по формуле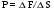 . (1.1) . (1.1)В общем случае гидромеханическое давление в данной точке равно пределу, к которому стремится отношение силы давления к площади  , ,на которую она действует, при уменьшении  Sдо нуля, Sдо нуля,т.е.при стягивании ее к точке 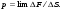 (1.2) (1.2)Если давление р отсчитывают от абсолютного нуля, то его называют абсолютным, а если отсчитывают от атмосферного давления ра, т. е. от условного нуля, то его называют избыточным (ризб) или манометрическим. Следовательно, абсолютное давление 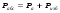 (1.3) (1.3)За единицу давления в Международной системе единиц (СИ) принят паскаль — давление, вызываемое силой 1Н, равномерно распределенной по нормальной к ней поверхности площадью 1 м2. Наряду с этой единицей давления применяют укрупненные единицы: килопаскаль (кПа) и мегапаскаль (МПа): 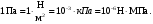 В технике в настоящее время продолжают применять также систему единиц МКГСС (метр, килограмм-сила, секунда), в которой за единицу давления принимается 1 кгс/м2. Используют также внесистемные единицы — техническую атмосферу и бар 1 ат=1 кгс/см2=10000 кгс/м2; 1 бар = 105 Па = 1, 02атм. Соотношение между единицами давления в системах СИ и МКГСС следующее: 1 Па = 0,102 кгс/м2 или 1 кгс/м2 = 9,81 Па. Касательное напряжение в жидкости, т. е. напряжение трения, обозначается буквой 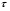 и выражается подобно давлению пределом и выражается подобно давлению пределом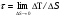 (1.4) (1.4)а размерность его та же, что и размерность давления. Основные свойства капельных жидкостей Одной из основных механических характеристик жидкости является ее плотность. Плотностью 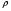 (кг/м3) называют массу жидкости, заключенную в единице объема; для однородной жидкости (кг/м3) называют массу жидкости, заключенную в единице объема; для однородной жидкости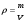 (1.5) (1.5)где m – масса жидкости в объеме V. Удельным весом 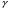 (Н/м3) называют вес единицы объема жидкости, т. е,. (Н/м3) называют вес единицы объема жидкости, т. е,.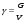 (1.6) (1.6)где G — вес жидкости в объеме V. Связь между удельным весом y и плотностью ρ легко найти, если учесть, что 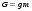 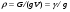 (1.7) (1.7)Если жидкость неоднородна, то формулы (1.4) и (1.5) определяют лишь среднее значение удельного веса или плотности в Данном объеме. Для определения истинного значения у и р в данной точке следует рассматривать объем, уменьшающийся до нуля, и искать предел соответствующего отношения. Применяют еще относительную плотность жидкости б, равную отношению плотности жидкости к плотности воды при 4 СС: б = ρж/ρвод (1.8) Коротко рассмотрим основные физические свойства капельных жидкостей. А) Сжимаемость, или свойство жидкости изменять свой объем под действием давления, характеризуется коэффициентом рр (м2/Н) объемного сжатия, который представляет собой относительное изменение объема, приходящееся на единицу давления, т. е. 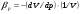 (1.9) (1.9)Знак минус в формуле обусловлен тем, что положительному приращению давления р соответствует отрицательное приращение (т. е. уменьшение) объема V. Рассматривая конечные приращения Δр = р - p1 и ΔV = V–V1 и считая βp постоянным, получаем 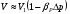 (1.10) (1.10)или, учитывая равенство (1.8), находим приближенную формулу для определения плотности 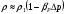 (1.11) (1.11)где ρ1 и ρ — плотности при давлениях p1 и р, Величина, обратная коэффициенту βр, представляет собой объемный модуль упругости K. Через модуль К и конечные разности формулу (1.8) можно переписать в виде зависимости ΔV/V = - Δр/ К (1.12) которую называют обобщенным законом Гука. Выразив объем через плотность, получим K = — dp/[ρd(1/ρ)] = ρ dρ /dρ или K/p = dp/dp = c2, (1.13) где с — скорость распространения продольных волн в упругой среде, равная скорости звука. Для капельных жидкостей модуль К несколько уменьшается с увеличением температуры и, возрастает с повышением давления. Для воды он составляет при атмосферном давлении приблизительно 2000 МПа. Следовательно, при повышении давления на 0,1 МПа объем воды уменьшается всего лишь на 1/20 000 часть. Такого же порядка модуль упругости и для других капельных жидкостей, например для минеральных масел он равен приблизительно 1200 МПа. Как следует из формулы (1.9), при повышении давления воды, например, до 40 МПа ее плотность повышается лишь на 2 %, а масла — на 3 %. Поэтому в большинстве случаев капельные жидкости можно считать практически несжимаемыми, т. е. принимать их плотность не зависящей от давления. Но при очень высоких давлениях и упругих колебаниях сжимаемость жидкостей следует учитывать. Различают адиабатный и изотермический модуль упругости. Первый больше второго приблизительно в 1,5 раза и проявляется при быстротечных процессах сжатия жидкости без теплообмена. Приведенные выше значения К являются значениями изотермического модуля. Б). Температурное расширение характеризуется коэффициентом рг объемного расширения, который представляет собой относительное изменение объема при изменении температуры Т на 1 °С и постоянном давлении, т. е. 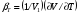 (1.14) (1.14)Рассматривая конечные приращения ΔV = V — Vlи ∆Т =Т – Т1и принимая βТ постоянным, получаем 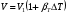 (1.15) (1.15)а учитывая равенство (1.8), находим приближенную формулу ρ = ρ1/(1 + βтΔТ) (1.16) где ρ1 и ρ — плотности при температурах Т1и Т. |
