Лекции. 1. Введение. 1 Предмет гидравлики и краткая история её развития
 Скачать 1.38 Mb. Скачать 1.38 Mb.
|
|
Потери напора при установившемся движении. Влияние различных факторов на движение жидкости Кинематика жидкости существенно отличается от кинематики твёрдого тела. Если отдельные частицы абсолютно твёрдого тела жёстко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют; эта среда состоит из множества частиц, движущихся одна относительно другой. Скорость в данной точке пространства, занятого движущейся жидкостью, является функцией координат этой точки, а иногда и времени. Рассмотрим движение идеальной жидкости, т.е. такой воображаемой жидкости, которая совершенно лишена вязкости. В такой не вязкой жидкости, так же как и в неподвижных реальных жидкостях, возможен лишь один вид напряжений - нормальные напряжения сжатия, т.е. гидромеханическое давление, или просто давление. Давление в движущейся идеальной жидкости обладает теми же свойствами, что и в неподвижной жидкости, т.е. на внешней поверхности жидкости оно направлено по внутренней нормали, а в любой точке жидкости - по всем направлениям одинаково. Течение жидкости может быть установившемся (стационарным) и неустановившемся (нестационарным). Установившемся называется течение жидкости, неизменное по времени, при котором давление и скорость являются функциями только координат, но не зависят от времени. Давление и скорость могут изменяться при перемещении частицы жидкости из одного положения в другое, но в данной неподвижной относительно русла точке давление и скорость при установившемся движении не изменяются по времени, т.е.: 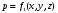 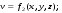 (1.46) (1.46)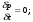 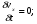 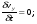 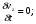 (1.47) (1.47)где индексы у скорости означают её проекции на соответствующие оси, жёстко связанные с руслом. Неустановившемся движением называется движение у которого все характеристики изменяются по времени в точках рассматриваемого характера. При неустановившемся течение траектории различных частиц, проходящих через данную точку пространства, могут иметь разную форму. Поэтому для рассмотрения картины течения, возникающей в каждый данный момент времени, вводится понятие линии тока. Линией тока называется кривая, в каждой точке которой вектор скорости в данный момент времени направлен по касательной. Если в движущейся жидкости взять бесконечно малый замкнутый контур и через все его точки провести линии тока, то образуется трубчатая поверхность, называемая трубкой тока. Часть потока, заключённая внутри трубки тока, называется элементарной струйкой. Живым сечением, или просто сечением потока, называется в общем случае поверхность в переделах потока, проведённая нормально к линиям тока. Далее будем рассматривать в потоках такие участки, в которых струйки можно считать параллельными и, следовательно, живые сечения - плоскими. Различают напорные и безнапорные течения жидкости. Напорными называют течения в закрытых руслах без свободной поверхности, а безнапорными - течения со свободной поверхностью. При напорных течениях давление вдоль потока обычно переменное, при безнапорном - постоянное (на свободной поверхности) и чаще всего атмосферное. Понятие о подобных потоках и критериях подобия Установление зависимости интересующей величины от системы выбранных определяющих факторов может выполняться двумя путями: аналитическим, основанным на законах механики и физики, и экспериментальным. Первый путь применим лишь для ограниченного числа задач и при том обычно лишь для упрощённых моделей явлений. Другой путь, экспериментальный, в принципе может учесть многие факторы, но он требует научно обоснованной постановки опытов, планирования эксперимента, ограничения его объёма необходимым минимумом и систематизацией результатов опытов. При этом должно быть обосновано моделирование явлений. Эти задачи позволяет решать так называемая теория гидродинамического подобия, т.е. подобия потоков несжимаемой жидкости. Гидродинамическое подобие складывается из трёх составляющих: геометрического подобия, кинематического и динамического. Геометрическое подобие представляет собой пропорциональность сходственных размеров и равенство соответствующих углов. В гидравлике под геометрическим подобием понимают подобие тех поверхностей, которые ограничивают потоки, т.е. подобие русел (или каналов). Кинематическое подобие означает пропорциональность местных скоростей в сходственных точках и равенство углов, характеризующих направление этих скоростей. Из кинематического подобия вытекает геометрическое подобие линий тока. Очевидно, что для кинематического подобия требуется геометрическое подобие русел. Динамическое подобие - это пропорциональность сил, действующих на сходственные объёмы в кинематически подобных потоках и равенство углов, характеризующих направление этих сил. Числа Рейнольдса, Фруда, Эйлера, Вебера Совокупность параметров, определяющих какой-либо гидродинамический процесс, можно рассматривать как конкретное решение дифференциальных уравнений этого процесса. Ему соответствуют вполне определённые начальные и граничные условия. Они представляют собой зависимости или константы, определяющие физические параметры в начальный момент и на границах во время движения. Следовательно, не только уравнения процесса, но также безразмерные формы начальных и граничных условий (условий однозначности) в механически подобных потоках должны быть одинаковыми. Имея это в виду, запишем уравнения Навье-Стокса и приведём их к безразмерному виду, для чего выберем характерные физические параметры L, V, T, P, F0 (если F - cила тяжести, то в качестве F0 удобно взять ускорение g свободного падения) и отнесём к ним соответствующие размерные величины: 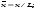 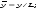 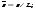 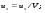 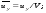 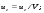 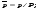 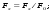 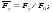 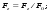 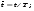 Для плотности и вязкости, которые считаем постоянными, характерные величины не выбираем, так как они сами ими являются. Примем также во внимание размерность дифференциальных операторов  и grad: и grad: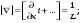 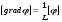 ; ;Векторное уравнение Навье-Стокса можно представить в виде 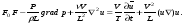 (1.48) (1.48)Чтобы придать этому уравнению безразмерный вид, разделим все его члены на коэффициент 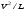 при конвективном ускорении. Получим при конвективном ускорении. Получим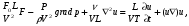 (1.49) (1.49)где дифференциальные операции выполняются по безразмерным переменным. В этом уравнение все члены, включая комбинации характерных параметров, безразмерны. Для всех динамических подобных потоков оно должно быть одинаковым, а следовательно, группы потоков были одинаковыми, т.е. 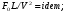 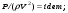 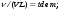 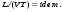 (1.50) (1.50)Входящие в условия (1.50) безразмерные комплексы играют роль критериев подобия и имеют следующие собственные наименования:  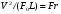 - число Фруда; - число Фруда; 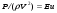 - число Эйлера; - число Эйлера; 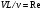 - число Рейнольдса; - число Рейнольдса; 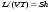 - число Струхала. - число Струхала.Понятие о гидравлических сопротивлениях, виды потерь напора (местные и по длине) Потери удельной энергии (напора), или, как их часто называют, гидравлические потери, зависят от формы, размеров русла, скорости течения и вязкости жидкости, а иногда и от абсолютного давления в ней. Вязкость жидкости, хотя и является первопричиной всех гидравлических потерь, но далеко не всегда оказывает существенное влияние на их величину. Гидравлические потери обычно разделяют на местные потери и потери на трение по длине. Местные потери энергии обусловлены так называемыми местными гидравлическими сопротивлениями (рис 1.18), т.е. местными изменениями формы и размеры русла, вызывающими деформацию потока. При протекании жидкости через местные сопротивления изменяется её скорость и обычно возникают крупные вихри. Последние образуются за местом отрыва потока от стенок и представляют собой области, в которых частицы жидкости движутся в основном по замкнутым кривым или близким к ним траекториям. 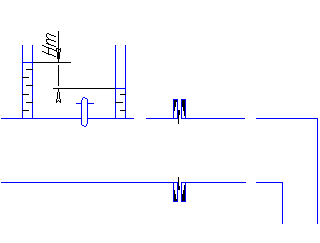 рис. 1.18 Пример местных гидравлических сопротивлений. Местные сопротивления напора определяются по формуле следующим образом: 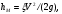 (1.51) (1.51)или в единицах давления 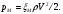 (1.52) (1.52)Выражение (1.5.4) часто называют формулой Вейсбаха. В ней V - средняя по сечению скорость в трубе, в которой установлено данное местное сопротивление. Потери на трение по длине - это потери энергии, которые в чистом виде возникают в прямых трубах постоянного сечения, т.е. при равномерном течении, и возрастают пропорционально длине трубы. Рассматриваемые потери обусловлены внутренним трением в жидкости, а потому имеют место не только в шероховатых, но и в гладких трубах. Потерю напора на трение можно выразить по общей формуле для гидравлического потерь, т.е. 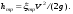 (1.53) (1.53)или 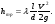 (1.54) (1.54)Общая формула для потерь напора по длине при установившемся равномерном движении жидкости. Коэффициент Дарси Как показывают опыты, во многих, но не во всех случаях гидравлические потери приблизительно пропорциональны скорости течения жидкости во второй степени, поэтому в гидравлике принят следующий общий способ выражения гидравлических потерь полного напора в линейных единицах: 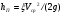 , или в единицах давления (1.55) , или в единицах давления (1.55)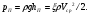 (1.56) (1.56)Такое выражение удобно тем, что включает в себя безразмерный коэффициент пропорциональности 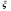 , называемый коэффициентом потерь Дарси или коэффициентом сопротивления. , называемый коэффициентом потерь Дарси или коэффициентом сопротивления.Основное уравнение равномерного движения Выделим некоторый отсек элементарной струйки (рис. 1.19). 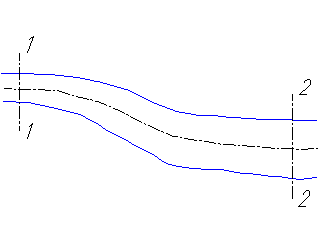 рис. 1.19 Объем элементарной струйки Во вход в это сечение в единицу времени втекает определённый объём жидкости, равный 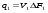 (1.57) (1.57)а через выход вытекает объём равный 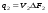 (1.58) (1.58)Примем, что жидкость несжимаема и что в ней невозможно образование незаполненных жидкостью пространств - пустот, т.е. будем считать, что соблюдается условие сплошности или неразрывности движения. Учитывая, что форма элементарной струйки с течением времени не изменяется и поперечный приток в струйку или отток из неё отсутствуют, приходим к выводу, что элементарные расходы жидкости, проходящие через вход и выход данного отрезка должны быть одинаковы. Таким образом, 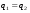 (1.59) (1.59)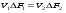 (1.60) (1.60)Подобные соотношения можно составить для любых отсеков элементарной струйки. Поэтому в более общем виде получаем, что всюду вдоль струйки 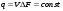 (1.61) (1.61)Полученное уравнение называется уравнением неразрывности; оно является первым основным уравнением гидродинамики. Касательные напряжения. Обобщённый закон Ньютона Согласно гипотезе, высказанной впервые Ньютоном в 1686 г., а затем экспериментально обоснованной проф. Н.П. Петровым в 1883 г., касательное напряжение в жидкости зависит от её рода и характера течения и при слоистом течении изменяется прямо пропорционально ьак называемому поперечному градиенту скорости. Таким образом 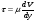 (1.62) (1.62)где 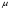 -коэффициент пропорциональности, получивший название динамической вязкости жидкости; -коэффициент пропорциональности, получивший название динамической вязкости жидкости; 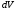 -приращение скорости, соответствующее приращению координаты -приращение скорости, соответствующее приращению координаты 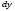 . .Поперечный градиент скорости 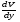 определяет изменение скорости, приходящееся на единицу длины в направлении нормали к стенке и, следовательно, характеризует интенсивность сдвига жидкости в данной точке (точнее определяет изменение скорости, приходящееся на единицу длины в направлении нормали к стенке и, следовательно, характеризует интенсивность сдвига жидкости в данной точке (точнее 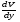 -это модуль градиента скорости; сам градиент – вектор). -это модуль градиента скорости; сам градиент – вектор).Ламинарный и турбулентный режимы движения жидкости. Критическое число Рейнольдса Опыты показывают, что возможны два режима или два вида течения жидкостей и газов в трубах: ламинарный и турбулентный. Ламинарным называется слоистое течение без перемешивания частиц жидкости и без пульсаций скоростей и давления. При таком течении все линии тока определяются формой русла, по которому течёт жидкость. При ламинарном течении жидкости в прямой трубе постоянного течения все линии тока направлены параллельно оси трубы, т.е. прямолинейно; отсутствуют поперечные перемещения жидкости. Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости и пульсациями скоростей и давлений. ёДвижение отдельных частиц оказывается подобным хаотическому, беспорядочному движению молекул газа. При турбулентном течении векторы скоростей имеют не только осевые, но и нормальные к оси русла составляющие, поэтому наряду с основным продольным перемещением жидкости вдоль русла происходят поперечные перемещения (перемешивание) и вращательное движение отдельных объёмов жидкости. Этим и объясняются пульсации скоростей и давления. Режим течения данной жидкости изменяется в данной трубе примерно при определённой средней по сечению скорости течения Vкр, которую называют критической. Как показывают опыты, значение этой скорости прямо пропорционально кинематической вязкости 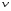 и обратно пропорционально диаметру d трубы, т.е. и обратно пропорционально диаметру d трубы, т.е.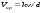 (1.63) (1.63)Входящий в эту формулу безразмерный коэффициент пропорциональности одинаков для всех жидкостей и газов, а также для любых параметров труб. Это означает, что изменение режима течения происходит при определённом соотношении между скоростью, диаметром и вязкостью 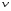 : :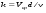 (1.64) (1.64)Этот результат согласуется с изложенной выше теорией гидродинамического подобия, и вполне закономерно, что именно число Рейнольдса является критерием, определяющим режим течения в трубах. Как показывают опыты, для труб круглого сечения 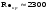 . .Таким образом, критерий подобия Рейнольдса позволяет судить о режиме течения жидкости в трубе. При 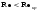 течение является ламинарным, при течение является ламинарным, при 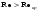 - турбулентным. - турбулентным.Смена режима течения обусловлена тем, что одно течение при достижении критического числа Рейнольдса теряет устойчивость, а другое - приобретает. Пульсации скоростей при турбулентном режиме. Мгновенная и местная осреднённые скорости Как было сказано в предыдущем пункте, для турбулентного течения характерны перемешивание жидкости пульсации скоростей и давлений. Скорость постоянно колеблется около осреднённого 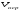 по времени значения. Траектории частиц, проходящих через данную неподвижную точку пространства в разные моменты времени, представляют собой кривые линии различной формы, несмотря на прямолинейность трубы. Таким образом, турбулентное течение всегда является неустановившемся, так как значения скоростей и давлений, а также траектории частиц, изменяются по времени. Однако его можно рассматривать как установившееся течение при условии, что осреднённые по времени значения скоростей и давлений, а также полный расход потока не изменяются со временем. по времени значения. Траектории частиц, проходящих через данную неподвижную точку пространства в разные моменты времени, представляют собой кривые линии различной формы, несмотря на прямолинейность трубы. Таким образом, турбулентное течение всегда является неустановившемся, так как значения скоростей и давлений, а также траектории частиц, изменяются по времени. Однако его можно рассматривать как установившееся течение при условии, что осреднённые по времени значения скоростей и давлений, а также полный расход потока не изменяются со временем.Распределение скоростей (осреднённых по времени) в поперечном сечении турбулентного потока существенно отличается от того, которое характерно для ламинарного течения. Если сравним кривые распределения скоростей в ламинарном и турбулентном потоках в одной и той же трубе и при одном и том же расходе (одинаковой средней скорости), то обнаружим существенное различие. Распределение скоростей при турбулентном течении более равномерно, а нарастание скорости у стенки более крутое, чем при ламинарном течении, для которого характерен параболический закон распределения скоростей. В связи с этим, коэффициент Кориолиса 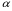 , учитывающий неравномерность распределения скоростей в уравнении Бернулли при турбулентном течении, значительно меньше, нежели при ламинарном. , учитывающий неравномерность распределения скоростей в уравнении Бернулли при турбулентном течении, значительно меньше, нежели при ламинарном.Потери напора по длине при равномерном ламинарном движении жидкости При ламинарном течении потеря напора на трение по длине при ламинарном течении пропорциональна скорости в первой степени [квадрат скорости в формуле (1.6.6) для ламинарного течения получен искусственно умножением и делением на 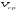 ], а коэффициент ], а коэффициент 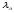 обратно пропорционален Re и, следовательно, скорости обратно пропорционален Re и, следовательно, скорости 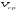 . .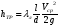 , (1.65) , (1.65)где 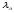 - коэффициент потерь на трение для ламинарного течения: - коэффициент потерь на трение для ламинарного течения: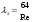 (1.66) (1.66)Распределение скоростей по живому сечению в цилиндрической трубе при ламинарном режиме. Коэффициент Дарси при ламинарном течении Если боковая поверхность трубы есть поверхность цилиндра, то естественно допустить существование ламинарного течения с линиями тока в виде прямых, параллельных образующим цилиндра. Для отыскания скорости имеем уравнение Пуассона с постоянной правой частью 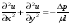 (1.67) (1.67)граничным условием которого является равенство нулю скорости не стенке трубы. В общем случае рассматриваемое течение может быть обусловлено как перепадом давления 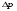 , так и осевым движением одного из цилиндров (речь идёт о рассмотрении цилиндрической трубы, состоящей из двух цилиндров (рис. 1.20)). , так и осевым движением одного из цилиндров (речь идёт о рассмотрении цилиндрической трубы, состоящей из двух цилиндров (рис. 1.20)).Допустим, что внутренний цилиндр перемещается в направлении оси z со скоростью 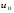 . Такому движению соответствуют граничные условия . Такому движению соответствуют граничные условия 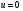 при при 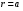 , , 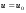 при при 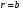 . Использовав их для определения постоянных . Использовав их для определения постоянных 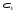 и и 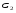 , найдём , найдём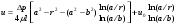 (1.68) (1.68)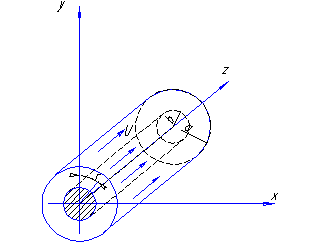 рис. 1.20 Цилиндрическая труба из двух цилиндров В частном случае, если перепада давления нет, то получим осесиммитричное течение Куэтта с распределением скоростей 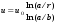 и касательными напряжениями в слое жидкости 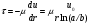 , ,где 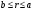 . .Из этой формулы следует, что если зазор между цилиндрами 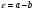 мал, то касательные напряжения в слое жидкости могут быть весьма значительными. мал, то касательные напряжения в слое жидкости могут быть весьма значительными.При неподвижных цилиндрах ( 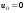 ) имеем течение в кольцевой трубе с распределением скоростей ) имеем течение в кольцевой трубе с распределением скоростей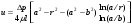 (1.69) (1.69)Эта зависимость позволяет вычислить все другие характеристики течения. В частности, расход 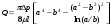 (1.70) (1.70)Разделив расход на площадь 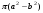 кольца, найдём выражение для средней скорости кольца, найдём выражение для средней скорости 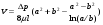 , (1.71) , (1.71)которое позволяет вычислять падение давления в кольцевой трубе. Потери напора при ламинарном течении также находятся по формуле Вейсбаха-Дарси: 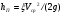 , (1.72) , (1.72)где 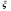 - безразмерный коэффициент пропорциональности, называемый коэффициентом потерь Дарси или коэффициентом сопротивления. - безразмерный коэффициент пропорциональности, называемый коэффициентом потерь Дарси или коэффициентом сопротивления.Потери напора при равномерном турбулентном движении жидкости Основной расчётной формулой для потерь напора при турбулентном течении в круглых трубах является уже приводимая формула Вейсбаха-Дарси и имеющая вид 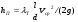 , (1.73) , (1.73)где 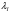 - коэффициент потерь на трение при турбулентном течении, или коэффициент Дарси. Существует ряд формул определяющих значение - коэффициент потерь на трение при турбулентном течении, или коэффициент Дарси. Существует ряд формул определяющих значение 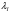 . Формула Конакова имеет вид . Формула Конакова имеет вид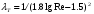 , (1.74) , (1.74)применима при числе Re от Reкр до Re, равного несколько миллионам. Формула Блазиуса имеет вид 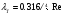 . (1.75) . (1.75)Механизм турбуллизации потока: процесс перемешивания жидкости, ядро течения и пристенный слой Движение отдельных частиц оказывается подобным хаотическому, беспорядочному движению молекул газа. При турбулентном течении векторы скоростей имеют не только осевые, но и нормальные к оси русла составляющие, поэтому наряду с основным продольным перемещением жидкости вдоль русла происходят поперечные перемещения (перемешивание) и вращательное движение отдельных объёмов жидкости. Так возникает перемешивание. Как показывают опыты ряда исследователей, при турбулентном течении жидкости непосредственно на стенке трубы обычно имеется ламинарный слой (рис 1.21). 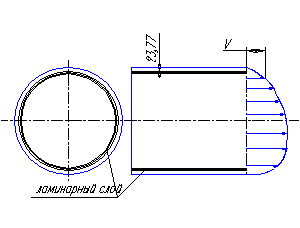 рис. 1.21 Ламинарный слой на стенке трубы Это очень тонкий слой жидкости, движение в котором является слоистым и происходит без перемешивания. В его пределах скорость круто нарастает от нуля на стенке до некоторой конечной величины 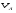 на границе слоя. Толщина на границе слоя. Толщина 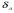 ламинарного слоя крайне невелика, причём оказывается, что число Re, подсчитанное по толщине ламинарного слоя крайне невелика, причём оказывается, что число Re, подсчитанное по толщине 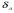 , скорости , скорости 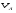 и кинематической вязкости и кинематической вязкости 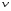 , есть величина постоянная, т.е. , есть величина постоянная, т.е.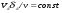 . (1.76) . (1.76)Эта величина в соответствии с теорией гидродинамического подобия имеет универсальное постоянное значение подобно тому, как постоянно Reкр для течения в трубах. Поэтому при увеличении скорости потока и, следовательно, Re растёт также скорость 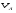 , а толщина , а толщина 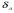 ламинарного слоя уменьшается. ламинарного слоя уменьшается.Коэффициент Дарси при турбулентном движении жидкости, экспериментальные методы его определения Для определения значений коэффициентов сопротивлений опытным путём может быть использована, например, установка, изображённая на рис. 1.22 установка состоит из центробежного насоса А, нагнетательной линии В, напорного резервуара С, снабжённого сливной линией D, опытного участка трубопровода Е, приёмного резервуара F и всасывающей линии G. Во время производства опытов жидкость насосом подаётся в напорный резервуар (в котором благодаря наличию сливной линии поддерживается постоянный уровень) и оттуда поступает в трубопровод. 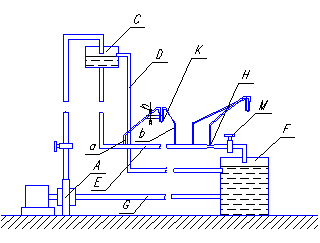 рис. 1.22 Установка для определения коэффициентов сопротивления Из трубопровода Е жидкость вытекает в приёмный резервуар и из него по всасывающей линии забирается насосом. Таким образом, во всё время опыта имеет место непрерывная циркуляция жидкости в системе. Измерение расхода жидкости Q осуществляется при помощи водометра Вентури H (в других случаях расход может быть замерен объёмным или весовым способом, для чего между трубопроводом и приёмным резервуаром вводится мерный бак). Линейные потери напора определяются по показанию дифференциального ртутного манометра K. Для большей надёжности измерений целесообразно установить два манометра, взаимно контролирующих друг друга. При этом следует иметь ввиду, что длина опытного участка трубопровода должна быть взята достаточно большой, так как при малой длине разность уровней в коленах ртутного манометра может оказаться незначительной и практически неощутимой; в подобных случаях вместо ртутного манометра необходимо применять дифференциальный пьезометр. При горизонтальном трубопроводе постоянного диаметра линейные потери напора по длине L между сечениями трубопровода a и b, к которым присоединён дифференциальный манометр, определяются выражением 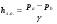 (1.77) (1.77)вспоминая, что 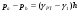 (1.78) (1.78)(где 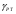 - удельный вес ртути, - удельный вес ртути, 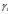 - удельный вес движущейся по трубопроводу жидкости, - удельный вес движущейся по трубопроводу жидкости, 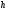 - разность уровней ртути в манометре), получаем: - разность уровней ртути в манометре), получаем: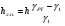 (1.79) (1.79)Из формулы Дарси-Вейсбаха имеем, далее, 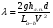 , (1.80) , (1.80)где потеря напора 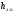 известна, а средняя скорость V может быть вычислена по измеренному расходу жидкости Q: известна, а средняя скорость V может быть вычислена по измеренному расходу жидкости Q: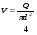 (1.81) (1.81)Измерения расхода и напора производятся несколько раз при различных скоростях движения жидкости по трубопроводу. После этого вычисляются соответствующие значения коэффициента 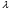 и числа Рейнольдса и строится кривая изменения коэффициента и числа Рейнольдса и строится кривая изменения коэффициента 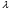 в зависимости от Re. в зависимости от Re. Для определения коэффициентов местного сопротивления в трубопроводе устанавливается на фланцах исследуемое сопротивление (расширяющийся или сужающийся патрубок, диафрагма и т.п.) и аналогично предыдущему находится полная потеря напора между сечениями a и b. Предварительно следует найти потерю напора в этом же трубопроводе, при той же самой скорости движения жидкости, но без местного сопротивления. Местная потеря напора 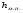 определяется как разность потерь напора в обоих случаях, после чего по формуле определяется как разность потерь напора в обоих случаях, после чего по формуле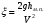 (1.82) (1.82)вычисляется значение коэффициента местного сопротивления. График Никурадзе Если для гидравлически гладких труб коэффициент потерь на трение вполне определяется числом Рейнольдса, то для шероховатых труб 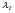 зависит ещё и от шероховатости внутренней поверхности трубы. При этом важен не абсолютный размер зависит ещё и от шероховатости внутренней поверхности трубы. При этом важен не абсолютный размер 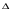 бугорков шероховатости, а отношение этого размера к радиусу (или диаметру) трубы, т.е. так называемая относительная шероховатость бугорков шероховатости, а отношение этого размера к радиусу (или диаметру) трубы, т.е. так называемая относительная шероховатость 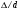 . Одна и та же абсолютная шероховатость может совершенно не оказывать влияния на сопротивление трубы большого диаметра, но способна значительно увеличить сопротивление трубы малого диаметра. Кроме того, на сопротивление влияет характер шероховатости. Простейшим случаем будет тот, когда все бугорки шероховатости имеют один и тот же размер . Одна и та же абсолютная шероховатость может совершенно не оказывать влияния на сопротивление трубы большого диаметра, но способна значительно увеличить сопротивление трубы малого диаметра. Кроме того, на сопротивление влияет характер шероховатости. Простейшим случаем будет тот, когда все бугорки шероховатости имеют один и тот же размер 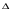 и одинаковую форму, т.е. при так называемой равномерно распределённой зернистой шероховатости. и одинаковую форму, т.е. при так называемой равномерно распределённой зернистой шероховатости.Таким образом, в этом случае коэффициент 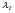 зависит как от Рейнольдса, так и от отношения зависит как от Рейнольдса, так и от отношения 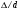 (или (или 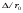 ): ):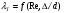 (1.83) (1.83)Характер влияния этих двух параметров на сопротивление труб отчётливо виден из графика, который является результатом опытов И.И. Никурадзе. 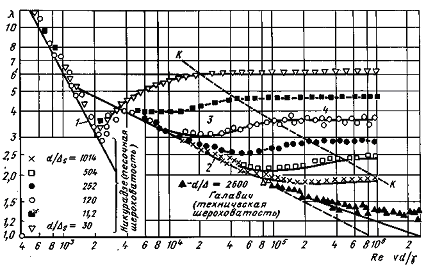 Рис 1.23. Экспериментальная зависимость гидравлического коэффициента трения А, от числа Рейнольдса 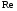 и относительной гладкости при песочной шероховатости (график Никурадзе) и относительной гладкости при песочной шероховатости (график Никурадзе)И.И. Никурадзе испытал на сопротивление ряд труб с искусственно созданной шероховатостью на их внутренней поверхности. Шероховатость была получена путём приклейки песчинок определённого размера,. Полученного просеиванием песка через специальные сита. Тем самым была получена равномерно распределённая зернистая шероховатость. Испытания были проведены при широком диапазоне относительных шероховатостей ( 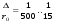 ), а также чисел ), а также чисел 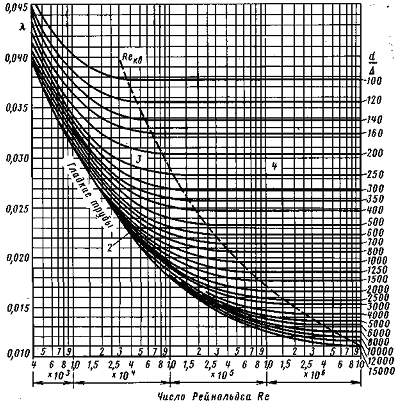 Рис. 2.24. Экспериментальные зависимости гидравлического коэффициента трения 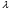 от числа Рейнольдса от числа Рейнольдса 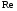 и относительной гладкости стенок для промышленных труб с неравномерной шероховатостью и относительной гладкости стенок для промышленных труб с неравномерной шероховатостьюRe ( 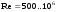 ). Результаты этих испытаний представлены в виде кривых зависимости ). Результаты этих испытаний представлены в виде кривых зависимости 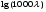 от от 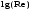 для ряда значений для ряда значений 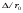 . .Из графика можно сделать следующие выводы:
Местные сопротивления, основные их виды При движении реальной жидкости помимо потерь на трение по длине потока могут возникать ещё так называемые местные потери напора. Причиной последних, например, в трубопроводах являются различного рода конструктивные вставки (колена, тройники, сужения и расширения трубопровода, задвижки, вентили и т.д.), необходимость установки которых вызывается условиями сооружения и эксплуатации трубопровода. Потери удельной энергии (напора), или, как их часто называют, гидравлические потери, зависят от формы, размеров русла, скорости течения и вязкости жидкости, а иногда и от абсолютного давления в ней. Вязкость жидкости, хотя и является первопричиной всех гидравлических потерь, но далеко не всегда оказывает существенное влияние на их величину. Гидравлические потери обычно разделяют на местные потери и потери на трение по длине. Местные потери энергии обусловлены так называемыми местными гидравлическими сопротивлениями (рис 1.5), т.е. местными изменениями формы и размеры русла, вызывающими деформацию потока. При протекании жидкости через местные сопротивления изменяется её скорость и обычно возникают крупные вихри. Последние образуются за местом отрыва потока от стенок и представляют собой области, в которых частицы жидкости движутся в основном по замкнутым кривым или близким к ним траекториям. Местные сопротивления вызывают изменение скорости движения жидкости по величине (сужение и расширение), направлению (колено) или величине и направлению одновременно (тройник). Поэтому часто указывают на некоторую аналогию между явлениями, происходящими в местных сопротивлениях, и явлениях в твёрдых телах, которое с механической точки зрения также характеризуется внезапным изменением скорости.  рис. 1.5 Пример местных гидравлических сопротивлений. Местные сопротивления напора определяются по формуле следующим образом: 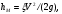 (1.84) (1.84)или в единицах давления 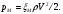 (1.85) (1.85)Выражение (1.84) часто называют формулой Вейсбаха. В ней V - средняя по сечению скорость в трубе, в которой установлено данное местное сопротивление. Потери на трение по длине - это потери энергии, которые в чистом виде возникают в прямых трубах постоянного сечения, т.е. при равномерном течении, и возрастают пропорционально длине трубы. Рассматриваемые потери обусловлены внутренним трением в жидкости, а потому имеют место не только в шероховатых, но и в гладких трубах. Потерю напора на трение можно выразить по общей формуле для гидравлического потерь, т.е. 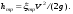 (1.86) (1.86)или 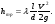 (1.87) (1.87)Общая формула для потерь напора по длине при установившемся равномерном движении жидкости. Коэффициент Дарси Как показывают опыты, во многих, но не во всех случаях гидравлические потери приблизительно пропорциональны скорости течения жидкости во второй степени, поэтому в гидравлике принят следующий общий способ выражения гидравлических потерь полного напора в линейных единицах: 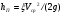 , или в единицах давления (1.5.7) , или в единицах давления (1.5.7)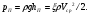 (1.5.8) (1.5.8)Такое выражение удобно тем, что включает в себя безразмерный коэффициент пропорциональности 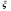 , называемый коэффициентом потерь Дарси или коэффициентом сопротивления. , называемый коэффициентом потерь Дарси или коэффициентом сопротивления. |
