Ответы на вопросы к коллоквиуму №2 (магнетизм). 1. Взаимодействие токов
 Скачать 1.04 Mb.
|
4. Теорема Гаусса для магнитного поля в вакууме (инт. и дифф. вид)Теорема Гаусса — основная теорема электродинамики, которая применяется для вычисления электрических полей, входит в систему уравнений Максвелла. Она выражает связь между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью. Общая формулировка: Поток вектора напряжённости электрического поля через любую, произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхностиэлектрическому заряду.  где
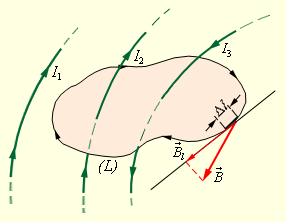
Данное выражение представляет собой теорему Гаусса в интегральной форме. В дифференциальной форме теорема Гаусса выражается следующим образом:  Здесь ρ — объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а — оператор набла. Для теоремы Гаусса справедлив принцип суперпозиции, то есть поток вектора напряжённости через поверхность не зависит от распределения заряда внутри поверхности. Физической основой теоремы Гаусса является закон Кулона или, иначе, теорема Гаусса является интегральной формулировкой закона Кулона. 5. Теорема о циркуляции для магнитного поля в вакууме (инт. и дифф. вид)Поясним понятие циркуляции вектора Пусть в пространстве, где создано магнитное поле, выбран некоторый условный замкнутый контур (не обязательно плоский) и указано положительное направление его обхода. На каждом отдельном малом участке Δl этого контура можно определить касательную составляющую вектора в данном месте, то есть определить проекцию вектора на направление касательной к данному участку контура (рис. 1.17.2).
Циркуляцией вектора называют сумму произведений Δl, взятую по всему контуру L:
Некоторые токи, создающие магнитное поле, могут пронизывать выбранный контур L в то время, как другие токи могут находиться в стороне от контура. Теорема о циркуляции утверждает, что циркуляция вектора магнитного поля постоянных токов по любому контуру L всегда равна произведению магнитной постоянной μ0 на сумму всех токов, пронизывающих контур:
В качестве примера на рис. 1.17.2 изображены несколько проводников с токами, создающими магнитное поле. Токи I2 и I3 пронизывают контур L в противоположных направлениях, им должны быть приписаны разные знаки – положительными считаются токи, которые связаны с выбранным направлением обхода контура правилом правого винта (буравчика). Следовательно, I3 > 0, а I2 < 0. Ток I1 не пронизывает контур L. Теорема о циркуляции в данном примере выражается соотношением:
Теорема о циркуляции в общем виде следует из закона Био–Савара и принципа суперпозиции. Простейшим примером применения теоремы о циркуляции является вывод формулы для магнитной индукции поля прямолинейного проводника с током. Учитывая симметрию в данной задаче, контур L целесообразно выбрать в виде окружности некоторого радиуса R, лежащей в перпендикулярной проводнику плоскости. Центр окружности находится в некоторой точке проводника. В силу симметрии вектор направлен по касательной , а его модуль одинаков во всех точках окружности. Применение теоремы о циркуляции приводит к соотношению:
откуда следует формула для модуля магнитной индукции поля прямолинейного проводника с током, приведенная ранее. Этот пример показывает, что теорема о циркуляции вектора магнитной индукции может быть использована для расчета магнитных полей, создаваемых симметричным распределением токов, когда из соображений симметрии можно «угадать» общую структуру поля. Имеется немало практически важных примеров расчета магнитных полей с помощью теоремы о циркуляции. Одним из таких примеров является задача вычисления поля тороидальной катушки |
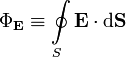— поток вектора напряжённости электрического поля через замкнутую поверхность S.