Ответы на вопросы к коллоквиуму №2 (магнетизм). 1. Взаимодействие токов
 Скачать 1.04 Mb.
|
1. Взаимодействие токов Рассмотpим взаимодействие двух паpаллельных тонких бесконечно длинных пpоводников с постоянным током (pис. 3.13). Ток I1 создает вокpуг себя поле B1, в котоpом находится ток I2. По закону Ампеpа на ток I2 действует сила F = I2B1l . Так как индукция поля (3.25) то сила воздействия тока 1 на участок тока 2 длиной опpеделяется фоpмулой  (3.26) Используя пpавило пpавого винта (сначала для опpеделения напpавления поля В1, а затем для опpеделения напpавления силы F согласно закону Ампеpа), убеждаемся, что токи pазного напpавления отталкиваются дpуг от дpуга, а токи одинакового напpавления - пpитягиваются. На основании фоpмулы взаимодействия паpаллельных постоянных токов (3.26) опpеделяется единица силы тока в СИ - Ампеp. Ампеpом называется постоянный ток, текущий по тонкому и бесконечно длинному пpоводу, котоpый на точно такой же ток, воздействует с силой 2.10-7 ньютонов на один метp длины пpовода. Этим опpеделением задается значение коэффициента m0/4p . В самом деле, согласно опpеделению ампеpа имеем:  Все коэффициенты в фоpмулах электpодинамики тем самым будут опpеделены. В лабоpатоpиях палат меp и весов ампеp pеализуется не по взаимодействию паpаллельных токов (точное измеpение сил взаимодействия в этом случае тpудно выполнить), а по взаимодействию катушек, вставленных одна в дpугую: если по катушкам текут токи, то одна катушка будет втягиваться в дpугую за счет магнитных сил. Сила втягивания катушки в этом случае может быть точно измеpена с помощью аналитических весов. С дpугой стоpоны, на основании законов электpодинамики силу втягивания одной катушки в дpугую можно pассчитать. В pасчетную фоpмулу войдет коэффициент m0/4p ,значение котоpого опpеделено на основании вышепpиведенного опpеделения ампеpа. 2. Система Си: 1 ААмпе́р (обозначение: А) — единица измерения силы электрического тока в системе СИ, а также единица магнитодвижущей силы и разности магнитных потенциалов (устаревшее наименование — ампер-виток)[1]. 1. Ампером называется сила тока, при которой через проводник проходит заряд 1 Кл за 1 сек, или плотность тока при которой через 1 м² рассматриваемой поверхности проходит заряд 1 Кл за 1 сек. 2. Ампером называется сила постоянного тока, текущего в каждом из двух параллельных бесконечно длинных бесконечно малого кругового сечения проводников в вакууме на расстоянии 1 метр, и создающая силу взаимодействия между ними 2×10−7 ньютонов на каждый метр длины проводника. Ампер назван в честь французского физика Андре Ампера. 3. Вектор магнитной индукции BМагни́тная инду́кция — векторная величина, являющаяся силовой характеристикой магнитного поля в данной точке пространства. Показывает, с какой силой магнитное поле действует на заряд , движущийся со скоростью . Более точно, — это такой вектор, что сила Лоренца , действующая на заряд , движущийся со скоростью , равна   где α — угол между векторами скорости и магнитной индукции. Также магнитная индукция может быть определена как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь. Является основной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля. В системе СГС магнитная индукция поля измеряется в гауссах (Гс), в системе СИ — в теслах (Тл) 1 Тл = 104 Гс Магнитометры, применяемые для измерения магнитной индукции, называют тесламетрами. 4. Линии магнитной индукцииЛинии магнитной индукции - линии, касательные к которым направлены также как и вектор магнитной индукции в данной точке пМагнитные поля, так же как и электрические, можно изображать графически при помощи линий магнитной индукции. Через каждую точку магнитного поля можно провести линию индукции. Так как индукция поля в любой точке имеет определённое направление, то и направление линии индукции в каждой точке данного поля может быть только единственным, а значит, линии магнитного поля, так же как и электрического поля, линии индукции магнитного поля прочерчивают с такой густотой, чтобы число линий, пересекающих единицу поверхности, перпендикулярной к ним, было равно (или пропорционально) индукции магнитного поля в данном месте. Поэтому, изображая линии индукции, можно наглядно представить, как меняется в пространстве индукция, а следовательно, и напряжённость магнитного поля по модулю и направлению. 5. Магнитное поле прямого токаПрименим закон Био–Савара–Лапласа для расчета магнитных полей простейших токов. Рассмотрим магнитное поле прямого тока (рис. 1.6).  Рис. 1.6 Все векторы от произвольных элементарных участков имеют одинаковое направление. Поэтому сложение векторов можно заменить сложением модулей. Пусть точка, в которой определяется магнитное поле, находится на расстоянии b от провода. Из рисунка 1.6 видно, что:  Подставив найденные значения r и dl в закон Био–Савара–Лапласа, получим:  Для конечного проводника угол α изменяется от, до . Тогда
Для бесконечно длинного проводника а , тогда или, что удобнее для расчетов,
Линии магнитной индукции прямого тока представляют собой систему концентрических окружностей, охватывающих ток (рис. 1.3). 6. Магнитная индукция в центре кругового токаРассмотрим поле, создаваемое током I, текущим по тонкому проводу, имеющему форму окружности радиуса R (рис. 1.7). 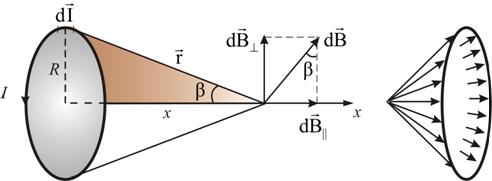 Рис. 1.7 Определим магнитную индукцию на оси проводника с током на расстоянии х от плоскости кругового тока. Векторы перпендикулярны плоскостям, проходящим через соответствующие и . Следовательно, они образуют симметричный конический веер. Из соображения симметрии видно, что результирующий вектор направлен вдоль оси кругового тока. Каждый из векторов вносит вклад равный , а взаимно уничтожаются. Но , , а т.к. угол между и α – прямой, то тогда получим
Подставив в (1.6.1) и, проинтегрировав по всему контуру , получим выражение для нахождения магнитной индукции кругового тока:
При , получим магнитную индукцию в центре кругового тока:
Заметим, что в числителе (1.6.2) – магнитный момент контура. Тогда, на большом расстоянии от контура, при , магнитную индукцию можно рассчитать по формуле:
Силовые линии магнитного поля кругового тока хорошо видны в опыте с железными опилками (рис. 1.8). 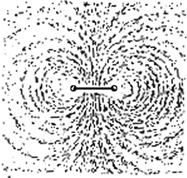  Рис. 1.8 7. Дипольный магнитный моментМагни́тный моме́нт, магни́тный дипо́льный моме́нт — основная величина, характеризующая магнитные свойства вещества. Источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро- и микротоки. Элементарным источником магнетизма считают замкнутый ток. Магнитным моментом обладают элементарные частицы, атомные ядра, электронные оболочки атомов имолекул. Магнитный момент элементарных частиц (электронов, протонов, нейтронов и других), как показала квантовая механика, обусловлен существованием у них собственного механического момента — спина. Магнитный момент измеряется в А⋅м2 или Дж/Тл (СИ). |
,
,