Ответы на вопросы к коллоквиуму №2 (магнетизм). 1. Взаимодействие токов
 Скачать 1.04 Mb. Скачать 1.04 Mb.
|
Формулы для вычисления магнитного моментаВ случае плоского контура с электрическим током магнитный момент вычисляется как , где I — сила тока в контуре, S — площадь контура, — единичный вектор нормали к плоскости контура. Направление магнитного момента обычно находится по правилу буравчика: если вращать ручку буравчика в направлении тока, то направление магнитного момента будет совпадать с направлением поступательного движения буравчика. Для произвольного замкнутого контура магнитный момент находится из: где — радиус-вектор, проведенный из начала координат до элемента длины контура В общем случае произвольного распределения токов в среде: 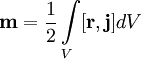 , ,где — плотность тока в элементе объёма dV. 8. Принцип суперпозицииЗа положительное направление вектора принимается направление от южного полюса S к северному полюсу N магнитной стрелки, свободно ориентирующийся в магнитном поле. Таким образом, исследуя магнитное поле, создаваемое током или постоянным магнитом, с помощью маленькой магнитной стрелки, можно в каждой точке пространства определить направление вектора . Направление этого вектора для поля прямого проводника с током и соленоида можно определить по правилу буравчика: если направление поступательного движения буравчика (винта) с правой нарезкой совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции. Модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением:
где μ0 – постоянная величина, которую называют магнитной постоянной. Ее численное значение равно μ0 = 4π∙10–7 H/A2 ≈ 1,26∙10–6 H/A2. Принцип суперпозиции магнитных полей: если магнитное поле создано несколькими проводниками с токами, то вектор магнитной индукции в какой-либо точке этого поля равен векторной сумме магнитных индукций, созданных в этой точке каждым током в отдельности:
9. Поток магнитного поляМагни́тный пото́к — поток как интеграл вектора магнитной индукции через конечную поверхность . Определяется через интеграл по поверхности 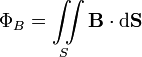 при этом векторный элемент площади поверхности определяется как где — единичный вектор, нормальный к поверхности. Также магнитный поток можно рассчитать как скалярное произведение вектора магнитной индукции на вектор площади: где α — угол между вектором магнитной индукции и нормалью к плоскости площади. Магнитный поток через контур также можно выразить через циркуляцию векторного потенциала магнитного поля по этому контуру: 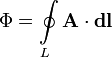 В системе СИ единицей магнитного потока является Вебер (Вб, размерность — В·с = кг·м²·с−2·А−1), в системе СГС — максвелл (Мкс); 1 Вб = 108 Мкс. 10. *Момент сил, действующих на контур с током в магнитном полеОпыт показывает, что момент сил, действующих на контур, зависит от его ориентации в пространстве, следовательно, физическая величина, описывающее магнитное поле, должна быть векторной. В общем случае этот вектор может изменяться от точки к точке, поэтому магнитное поле должно описываться математически как уже знакомое нам векторной поле. Так как мы хотим определить «точечную» характеристику магнитного поля, то такой контур (или магнитную стрелку) следует считать бесконечно малым. В очередной раз мы должны сделать традиционную оговорку – бесконечно малый контур физически нереализуем – даже провода имеют конечную толщину, поэтому переход к бесконечно малому контуру следует понимать в физическом смысле – мал, настолько, что с математической точки можно считать бесконечно малым, но реально реализуемым. Чтобы избавиться от неоднозначности измеряемого момента сил, связанной с ориентацией контура, выберем такое положение контура, при котором модель момента сил максимален Mmax. Наконец, учтем еще один экспериментальный факт –момент сил, действующих на контур, пропорционален силе тока в контуре I и площади контура S. Следовательно, отношение момента сил к произведению силы тока в контуре на его площадь является величиной, не зависящей от свойств контура, поэтому является характеристикой поля, которая называется индукцией магнитного поля 11.*Энергия контура с током в магнитном полеЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА Вокруг проводника с током существует магнитное поле, которое обладает энергией. Откуда она берется? Источник тока, включенный в эл.цепь, обладает запасом энергии. В момент замыкания эл.цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля. Энергия магнитного поля равна собственной энергии тока. Собственная энергия тока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи. 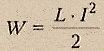 Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока. Куда пропадает энергия магнитного поля после прекращения тока? - выделяется ( при размыкании цепи с достаточно большой силой тока возможно возникновение искры или дуги) 12.*Работа, совершаемая при перемещении тока в магнитном полеРассмотрим контур с током, образованный неподвижными проводами и скользящей по ним подвижной перемычкой длиной l (рис. 2.17). Этот контур находится во внешнем однородном магнитном поле , перпендикулярном к плоскости контура. При показанном на рисунке направлении тока I, вектор сонаправлен с . 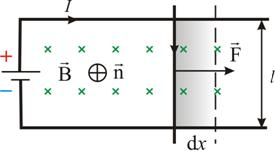 Рис. 2.17 На элемент тока I (подвижный провод) длиной l действует сила Ампера, направленная вправо: Пусть проводник l переместится параллельно самому себе на расстояние dx. При этом совершится работа: Итак,
Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником. Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции. Выведем выражение для работы по перемещению замкнутого контура с током в магнитном поле. Рассмотрим прямоугольный контур с током 1-2-3-4-1 (рис. 2.18). Магнитное поле направлено от нас перпендикулярно плоскости контура. Магнитный поток , пронизывающий контур, направлен по нормали к контуру, поэтому . 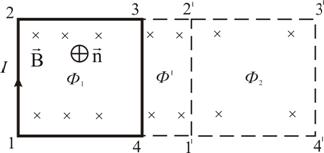 Рис. 2.18 Переместим этот контур параллельно самому себе в новое положение 1'-2'-3'-4'-1'. Магнитное поле в общем случае может быть неоднородным и новый контур будет пронизан магнитным потоком . Площадка 4-3-2'-1'-4, расположенная между старым и новым контуром, пронизывается потоком . Полная работа по перемещению контура в магнитном поле равна алгебраической сумме работ, совершаемых при перемещении каждой из четырех сторон контура: где , равны нулю, т.к. эти стороны не пересекают магнитного потока, при своём перемещение (очерчивают нулевую площадку). . Провод 1–2 перерезает поток ( ), но движется против сил действия магнитного поля. . Тогда общая работа по перемещению контура или
здесь – это изменение магнитного потока, сцепленного с контуром. Работа, совершаемая при перемещении замкнутого контура с током в магнитном поле, равна произведению величины тока на изменение магнитного потока,сцепленного с этим контуром. Элементарную работу по бесконечно малому перемещению контура в магнитном поле можно найти по формуле
Выражения (2.9.1) и (2.9.5) внешне тождественны, но физический смысл величины dФ различен. Соотношение (2.9.5), выведенное нами для простейшего случая, остаётся справедливым для контура любой формы в произвольном магнитном поле. Более того, если контур неподвижен, а меняется , то при изменении магнитного потока в контуре на величину dФ, магнитное поле совершает ту же работу 13. МагнетикиМагнитные материалы, Магнетики — материалы, вступающие во взаимодействие с магнитным полем, выражающееся в его изменении, а также в других физических явлениях — изменение физических размеров, температуры, проводимости, возникновению электрического потенциала и т. д. К магнитным материалам относят вещества, обладающие определенными магнитными свойствами и используемые в современной технологии. Магнитными материалами могут быть различные сплавы, химические соединения, жидкости. В основном магнитные материалы делят на две большие группы - Магнитотвёрдые материалы и Магнитомягкие материалы. В то же время в связи с успехом в науках изучающих магнетизм и с развитием большой исследовательской работы в области изучения магнитных материалов, появились новые большие группы магнитных материалов: магнитострикционные материалы, магнитооптические материалы, термомагнитные материалы. |
