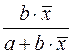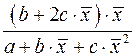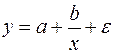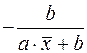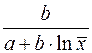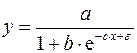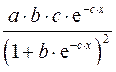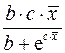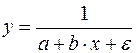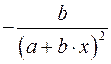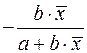ЭКОНОМЕТРИКА ОТВЕТЫ. 1. Задачи эконометрики в области социальноэкономических исследований

• Название: 1. Задачи эконометрики в области социальноэкономических исследований
• Анкор: ЭКОНОМЕТРИКА ОТВЕТЫ.docx
• Дата: 17.01.2018
• Размер: 0.56 Mb.
• Имя файла: ЭКОНОМЕТРИКА ОТВЕТЫ.docx
• Тип: Документы; #14366
• страница: 3 из 4

16.Частные уравнения регрессии. Частные коэффициенты корреляции

На основе уравнения (2.1) могут быть найдены частные уравнения регрессии: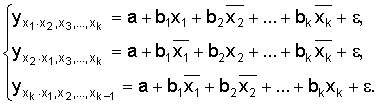

. (2.4)

Частные уравнения регрессии характеризуют изолированное влияние фактора, при условии, что остальные закреплены на неизменном уровне.

Если в (2.4) подставить 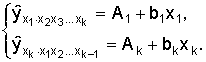, то система (2.4) будет иметь вид:



Частные коэффициенты (или индексы) корреляциихарактеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии.

Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.

Предположим, что зависимость y x₁ характеризуется уравнением

y_x1 = b₀ + b₁ × x₁.

Подставив в это уравнение фактическое значение x₁, найдем теоретические величины и соответствующую величину остаточной дисперсии s²:

.

Включив в уравнение регрессии дополнительный фактор x₂, получим уравнение регрессии вида

y_x1x2 = b₀ + b₁ × x₁ + b₂ × x₂.

Для этого уравнения остаточная дисперсия, естественно, меньше. Чем большее число факторов включено в модель, тем меньше величина остаточной дисперсии, т.е. происходит ее сокращение. Чем больше доля этого сокращения в остаточной вариации до введения дополнительного фактора, тем теснее связь между y и x₂ при постоянном действии фактора x₁. Корень квадратный из этой величины и есть индекс частной корреляции, показывающий в «чистом» виде тесноту связи y с x₂.

Следовательно, чистое влияние фактора x₂ на результат y можно найти как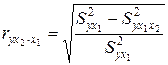

. (3.19)

Знак «точка» в выражении частного коэффициента корреляции r_yx2×x1 означает элиминирование той переменной (переменных), которая стоит после знака «точка».

Аналогично определяется и чистое влияние на результат y фактора x₁: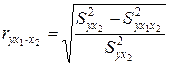

. (3.20)

Если выразить остаточную дисперсию через скорректированный показатель детерминации S²_ост = S²_y (1 – R²), то формула коэффициента частной корреляции примет вид: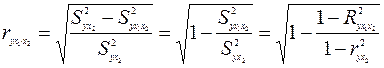

. (3.21)

Соответственно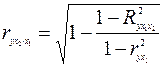

. (3.22)

Рассмотренные показатели частной корреляции принято называть коэффициентами (индексами) частной корреляции первого порядка, ибо они фиксируют тесноту связи двух переменных при закреплении (элиминировании влияния) одного фактора.

Если рассматривается регрессия с числом факторов р, то возможны частные коэффициенты корреляции не только первого, но и второго, третьего, ..., (р – 1) порядка, т. е. влияние фактора x₁ можно оценить при разных условиях независимости действия других факторов:

r_yx1×x2 – при постоянном действии фактора x²

r_yx1×x2x3 – при постоянном действии факторов x² и x³

r_yx1×x2…xp – при неизменном действии всех факторов,

включенных в уравнение регрессии

Сопоставление коэффициентов частной корреляции разных порядков по мере увеличения числа включаемых факторов показывает процесс «очищения» связи результативного признака с исследуемым фактором.

Хотя частная корреляция разных порядков и может представлять аналитический интерес, в практических исследованиях предпочтение отдают показателям частной корреляции самого высокого порядка, ибо именно эти показатели являются дополнением к уравнению множественной регрессии.

В общем виде при наличии р факторов для уравнения

y = b₀ + b₁ × x₁ + b₂ × x₂ + … + b_p × x_p + e.

коэффициент частной корреляции, измеряющий влияние на у фактора x_i; при неизменном уровне других факторов, можно определить по формуле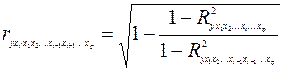

. (3.23)

где – множественный коэффициент детерминации всего комплекса р факторов с результатом; – тот же показатель детерминации, но без введения в модель фактора x_i.

Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Например, r_yx1×x2 – коэффициент частной корреляции первого порядка. Соответственно коэффициенты парной корреляции называются коэффициентами нулевого порядка. Коэффициенты частной корреляции более высоких порядков можно найти через коэффициенты частной корреляции более низких порядков по рекуррентной формуле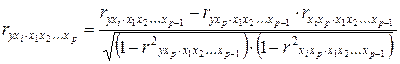

. (3.25)

При двух факторах и i = 1 данная формула примет вид: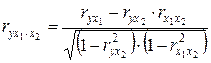

. (3.26)

Соответственно при i = 2 и двух факторах частный коэффициент корреляции у с фактором x₂ можно определить по формуле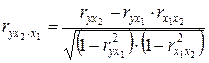

. (3.27)

В эконометрике частные коэффициенты корреляции обычно не имеют самостоятельного значения. В основном их используют на стадии формирования модели, в частности в процедуре отсева факторов. Так, при построении многофакторной модели, например, методом исключения переменных на первом шаге определяется уравнение регрессии с полным набором факторов и рассчитывается матрица частных коэффициентов корреляции. На втором шаге отбирается фактор с наименьшей и несущественной по t- критерию Стьюдента величиной показателя частной корреляции. Исключив его из модели, строят новое уравнение регрессии. Процедура продолжается до тех пор, пока не окажется, что все частные коэффициенты корреляции существенно отличаются от нуля. Если исключен несущественный фактор, то множественные коэффициенты детерминации на двух смежных шагах построения регрессионной модели почти не отличаются друг от друга, т.е. R²_p+1 » R²_p, где p – число факторов.

Из формул частных коэффициентов корреляции видна связь этих показателей с совокупным коэффициентом корреляции. Зная частные коэффициенты корреляции (последовательно первого, второго и более высокого порядка), можно определить совокупный коэффициент корреляции по формуле

. (3.31)

При полной зависимости результативного признака от исследуемых факторов коэффициент совокупного влияния их равен единице. Из единицы вычитается доля остаточной вариации признак (1 – r²), обусловленная последовательно включенными в анализ факторами. В результате подкоренное выражение характеризует совокупное действие всех исследуемых факторов.

Для уравнения регрессии прибыли y = –4,874 + 0,585 x₁ +0,240 x₂ + e данный подход расчета коэффициента множественной корреляции приведет к следующей его величине:

,

т.е. получен тот де результат, что и ранее.

17.Частные уравнения регрессии. Частные коэффициенты эластичности

На основе уравнения (2.1) могут быть найдены частные уравнения регрессии: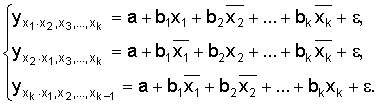

. (2.4)

Частные уравнения регрессии характеризуют изолированное влияние фактора, при условии, что остальные закреплены на неизменном уровне.

Если в (2.4) подставить 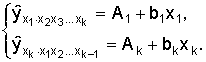, то система (2.4) будет иметь вид:



коэффициентов эластичности для различных типов уравнений регрессии.

В зависимости от вида зависимости между х и у формулы расчета коэффициентов эластичности будут меняться. Основные формулы для наиболее часто используемых типов уравнений регрессии приведены в таблице:

Вид функции,	Первая производная,	Средний коэффициент эластичности,

Только для степенных функций коэффициент эластичности представляет собой постоянную независящую от х величину, равную в данном случае параметру b.

Возможны случаи, когда расчет коэффициента эластичности не имеет смысла. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения в процентах. Например, на сколько процентов изменится заработная плата с ростом стажа работы на 1%? В такой ситуации степенная функция, даже если она оказывается наилучшей, не может быть экономически интерпретирована. Например, изучая соотношение ставок межбанковского кредита у (в процентах годовых) и срока его предоставления х (в днях), было получено уравнение регрессии с очень высоким показателем корреляции (0,98). Коэффициент эластичности 0,352% лишен смысла, ибо срок предоставления кредита не измеряется в процентах. Значительно больший интерес для этой зависимости может представить линейная функция , имеющая более низкий показатель корреляции 0,85. Коэффициент регрессии 0,403 показывает (в процентах) изменение ставок кредита с увеличением срока его предоставления на один день.

В линейной модели множественной регрессии если факторные признаки различны по своей сущности или имеют различные единицы измерения, коэффициенты регрессии b_j являются несопоставимыми. Поэтому уравнение регрессии дополняют соизмеримыми показателями тесноты связи фактора с результатом, позволяющими ранжировать факторы по силе влияния на результат. К таким показателям относятся частные коэффициенты эластичности.

Частные коэффициенты эластичности рассчитываются по формуле: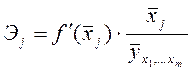

,

где - среднее значение фактора ;

- среднее значение результата у.

Частный коэффициент эластичности показывает, насколько процентов в среднем изменяется результат у с увеличением фактора на 1% от своего среднего уровня при фиксированном положении других факторов модели. В случае линейной зависимости коэффициенты эластичности рассчитываются по формуле: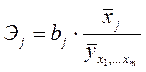



где – коэффициент регрессии для фактора в уравнении множественной регрессии.

Наряду с частными коэффициентами эластичности могут быть найдены средние по совокупности показатели эластичности: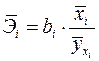

,

которые показывают, на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.