ЭКОНОМЕТРИКА ОТВЕТЫ. 1. Задачи эконометрики в области социальноэкономических исследований
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
Линейная модель парной регрессии и корреляции 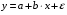 . .Построение линейной регрессии сводится к оценке ее параметров – 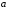 и и 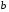 . Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров . Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров 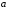 и и 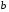 , при которых сумма квадратов отклонений фактических значений результативного признака , при которых сумма квадратов отклонений фактических значений результативного признака 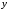 от теоретических от теоретических 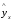 минимальна: минимальна: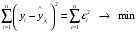 . .свойства оценок, полученных с помощью МНК:
Теорема Гаусса-Маркова: если выполнены условия Гаусса-Маркова, тогда оценки , полученные с помощью метода наименьших квадратов, являются линейными, несмещёнными, эффективными и состоятельными оценками. 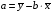 , , 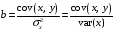 , где ковариация признаков , где ковариация признаков 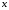 и и 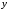 , , 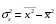 – дисперсия признака – дисперсия признака 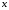 и и Ковариация – числовая характеристика совместного распределения двух случайных величин, равная математическому ожиданию произведения отклонений этих случайных величин от их математических ожиданий. Дисперсия – характеристика случайной величины, определяемая как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Математическое ожидание – сумма произведений значений случайной величины на соответствующие вероятности. Параметр 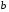 называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.Формально 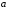 – значение – значение 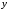 при при 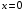 . .Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции 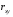 , который можно рассчитать по следующим формулам: , который можно рассчитать по следующим формулам: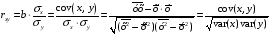 . (1.6) . (1.6)Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции 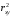 , называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака , называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака 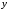 , объясняемую регрессией, в общей дисперсии результативного признака. , объясняемую регрессией, в общей дисперсии результативного признака. 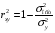 Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации. не должна превышать 8–10%. После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров. Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной. на основе 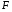 -критерия Фишера, которому предшествует дисперсионный анализ. -критерия Фишера, которому предшествует дисперсионный анализ. 13.Сравнение истинных и оцененных зависимостей 14.Множественная линейная регрессия Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Если же этим влиянием пренебречь нельзя, то в этом случае следует попытаться выявить влияние других факторов, введя их в модель, т.е. построить уравнение множественной регрессии  , ,где  – зависимая переменная (результативный признак), – зависимая переменная (результативный признак), 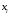 – независимые, или объясняющие, переменные (признаки-факторы). – независимые, или объясняющие, переменные (признаки-факторы).2.1. Спецификация модели. Отбор факторов при построении уравнения множественной регрессии Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Он включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии. Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям.
Отбор факторов производится на основе качественного теоретико-экономического анализа. Однако теоретический анализ часто не позволяет однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых признаков и целесообразности включения фактора в модель. Поэтому отбор факторов обычно осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй – на основе матрицы показателей корреляции определяют статистики для параметров регрессии. Коэффициенты интеркорреляции (т.е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если 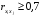 . Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга. . Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга.По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга. Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов. Существует ряд подходов преодоления сильной межфакторной корреляции. Самый простой путь устранения мультиколлинеарности состоит в исключении из модели одного или нескольких факторов. Другой подход связан с преобразованием факторов, при котором уменьшается корреляция между ними. При отборе факторов также рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6–7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то число степеней свободы остаточной дисперсии очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а 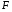 -критерий меньше табличного значения. -критерий меньше табличного значения.15.Показатели качества регрессии Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – показателя детерминации. Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком или, иначе, оценивает тесноту совместного влияния факторов на результат. Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции: 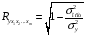 . (2.12) . (2.12)Границы изменения индекса множественной корреляции от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции: 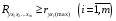 . .Расчет индекса множественной корреляции предполагает определение уравнения множественной регрессии и на его основе остаточной дисперсии: 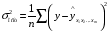 . (2.13) . (2.13)Можно пользоваться следующей формулой индекса множественной детерминации: 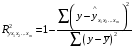 . (2.14) . (2.14)При линейной зависимости признаков формула индекса множественной корреляции может быть представлена следующим выражением: 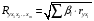 , (2.15) , (2.15)где 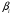 – стандартизованные коэффициенты регрессии; – стандартизованные коэффициенты регрессии; 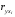 – парные коэффициенты корреляции результата с каждым фактором. – парные коэффициенты корреляции результата с каждым фактором.Формула индекса множественной корреляции для линейной регрессии получила название линейного коэффициента множественной корреляции, или, что то же самое, совокупного коэффициента корреляции. Возможно также при линейной зависимости определение совокупного коэффициента корреляции через матрицу парных коэффициентов корреляции: 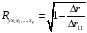 , (2.16) , (2.16)где 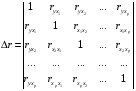 – определитель матрицы парных коэффициентов корреляции; 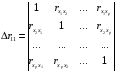 – определитель матрицы межфакторной корреляции. В рассмотренных показателях множественной корреляции (индекс и коэффициент) используется остаточная дисперсия, которая имеет систематическую ошибку в сторону преуменьшения, тем более значительную, чем больше параметров определяется в уравнении регрессии при заданном объеме наблюдений 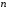 . Если число параметров при . Если число параметров при 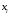 равно равно 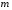 и приближается к объему наблюдений, то остаточная дисперсия будет близка к нулю и коэффициент (индекс) корреляции приблизится к единице даже при слабой связи факторов с результатом. Для того чтобы не допустить возможного преувеличения тесноты связи, используется скорректированный индекс (коэффициент) множественной корреляции. и приближается к объему наблюдений, то остаточная дисперсия будет близка к нулю и коэффициент (индекс) корреляции приблизится к единице даже при слабой связи факторов с результатом. Для того чтобы не допустить возможного преувеличения тесноты связи, используется скорректированный индекс (коэффициент) множественной корреляции.Скорректированный индекс множественной корреляции содержит поправку на число степеней свободы, а именно остаточная сумма квадратов 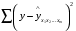 делится на число степеней свободы остаточной вариации делится на число степеней свободы остаточной вариации 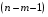 , а общая сумма квадратов отклонений , а общая сумма квадратов отклонений 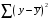 на число степеней свободы в целом по совокупности на число степеней свободы в целом по совокупности 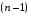 . .Формула скорректированного индекса множественной детерминации имеет вид: 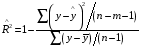 , (2.17) , (2.17)где 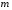 – число параметров при переменных – число параметров при переменных 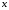 ; ; 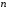 – число наблюдений. – число наблюдений.Поскольку 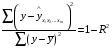 , то величину скорректированного индекса детерминации можно представить в виде: , то величину скорректированного индекса детерминации можно представить в виде: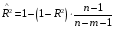 . (2.17а) . (2.17а)Чем больше величина 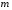 , тем сильнее различия , тем сильнее различия 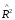 и и 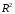 . .Как было показано выше, ранжирование факторов, участвующих во множественной линейной регрессии, может быть проведено через стандартизованные коэффициенты регрессии ( 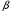 -коэффициенты). Эта же цель может быть достигнута с помощью частных коэффициентов корреляции (для линейных связей). Кроме того, частные показатели корреляции широко используются при решении проблемы отбора факторов: целесообразность включения того или иного фактора в модель можно доказать величиной показателя частной корреляции. -коэффициенты). Эта же цель может быть достигнута с помощью частных коэффициентов корреляции (для линейных связей). Кроме того, частные показатели корреляции широко используются при решении проблемы отбора факторов: целесообразность включения того или иного фактора в модель можно доказать величиной показателя частной корреляции.Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании (устранении влияния) других факторов, включенных в уравнение регрессии. Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель. В общем виде при наличии 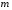 факторов для уравнения факторов для уравнения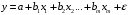 коэффициент частной корреляции, измеряющий влияние на 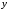 фактора фактора 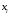 , при неизменном уровне других факторов, можно определить по формуле: , при неизменном уровне других факторов, можно определить по формуле: , (2.18) , (2.18)где 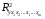 – множественный коэффициент детерминации всех – множественный коэффициент детерминации всех 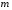 факторов с результатом; факторов с результатом; 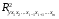 – тот же показатель детерминации, но без введения в модель фактора – тот же показатель детерминации, но без введения в модель фактора 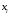 . .При двух факторах формула (2.18) примет вид: 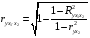 ; ; 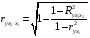 . (2.18а) . (2.18а)Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Например, 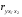 – коэффициент частной корреляции первого порядка. Соответственно коэффициенты парной корреляции называются коэффициентами нулевого порядка. Коэффициенты частной корреляции более высоких порядков можно определить через коэффициенты частной корреляции более низких порядков по рекуррентной формуле: – коэффициент частной корреляции первого порядка. Соответственно коэффициенты парной корреляции называются коэффициентами нулевого порядка. Коэффициенты частной корреляции более высоких порядков можно определить через коэффициенты частной корреляции более низких порядков по рекуррентной формуле: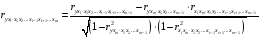 . (2.19) . (2.19)При двух факторах данная формула примет вид: 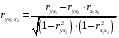 ; ; 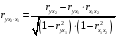 . (2.19а) . (2.19а)Для уравнения регрессии с тремя факторами частные коэффициенты корреляции второго порядка определяются на основе частных коэффициентов корреляции первого порядка. Так, по уравнению 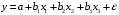 возможно исчисление трех частных коэффициентов корреляции второго порядка: возможно исчисление трех частных коэффициентов корреляции второго порядка: , , 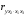 , , 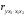 , ,каждый из которых определяется по рекуррентной формуле. Например, при 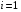 имеем формулу для расчета имеем формулу для расчета  : :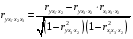 . (2.20) . (2.20)Рассчитанные по рекуррентной формуле частные коэффициенты корреляции изменяются в пределах от –1 до +1, а по формулам через множественные коэффициенты детерминации – от 0 до 1. Сравнение их друг с другом позволяет ранжировать факторы по тесноте их связи с результатом. Частные коэффициенты корреляции дают меру тесноты связи каждого фактора с результатом в чистом виде. Если из стандартизованного уравнения регрессии 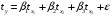 следует, что следует, что 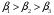 , т.е. no силе влияния на результат порядок факторов таков: , т.е. no силе влияния на результат порядок факторов таков: 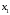 , , 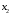 , , 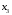 , то этот же порядок факторов определяется и по соотношению частных коэффициентов корреляции, , то этот же порядок факторов определяется и по соотношению частных коэффициентов корреляции, 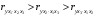 . .Из приведенных выше формул частных коэффициентов корреляции видна связь этих показателей с совокупным коэффициентом корреляции. Зная частные коэффициенты корреляции (последовательно первого, второго и более высокого порядка), можно определить совокупный коэффициент корреляции по формуле: 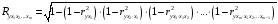 . (2.21) . (2.21)В частности, для двухфакторного уравнения формула (2.21) принимает вид: 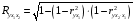 . (2.21) . (2.21)При полной зависимости результативного признака от исследуемых факторов коэффициент совокупного их влияния равен единице. Из единицы вычитается доля остаточной вариации результативного признака 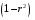 , обусловленная последовательно включенными в анализ факторами. В результате подкоренное выражение характеризует совокупное действие всех исследуемых факторов. , обусловленная последовательно включенными в анализ факторами. В результате подкоренное выражение характеризует совокупное действие всех исследуемых факторов.Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью 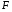 -критерия Фишера: -критерия Фишера: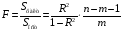 , (2.22) , (2.22)где 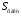 – факторная сумма квадратов на одну степень свободы; – факторная сумма квадратов на одну степень свободы; 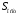 – остаточная сумма квадратов на одну степень свободы; – остаточная сумма квадратов на одну степень свободы; 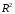 – коэффициент (индекс) множественной детерминации; – коэффициент (индекс) множественной детерминации; 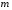 – число параметров при переменных – число параметров при переменных 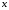 (в линейной регрессии совпадает с числом включенных в модель факторов); (в линейной регрессии совпадает с числом включенных в модель факторов); 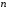 – число наблюдений. – число наблюдений.Оценивается значимость не только уравнения в целом, но и фактора, дополнительно включенного в регрессионную модель. Необходимость такой оценки связана с тем, что не каждый фактор, вошедший в модель, может существенно увеличивать долю объясненной вариации результативного признака. Кроме того, при наличии в модели нескольких факторов они могут вводиться в модель в разной последовательности. Ввиду корреляции между факторами значимость одного и того же фактора может быть разной в зависимости от последовательности его введения в модель. Мерой для оценки включения фактора в модель служит частный 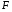 -критерий, т.е. -критерий, т.е. 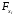 . .Частный 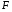 -критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включенного фактора, с остаточной дисперсией на одну степень свободы по регрессионной модели в целом. В общем виде для фактора -критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включенного фактора, с остаточной дисперсией на одну степень свободы по регрессионной модели в целом. В общем виде для фактора 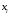 частный частный 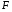 -критерий определится как -критерий определится как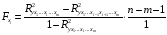 , (2.23) , (2.23)где 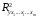 – коэффициент множественной детерминации для модели с полным набором факторов, – коэффициент множественной детерминации для модели с полным набором факторов, 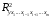 – тот же показатель, но без включения в модель фактора – тот же показатель, но без включения в модель фактора 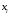 , , 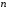 – число наблюдений, – число наблюдений, 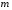 – число параметров в модели (без свободного члена). – число параметров в модели (без свободного члена).Фактическое значение частного 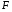 -критерия сравнивается с табличным при уровне значимости -критерия сравнивается с табличным при уровне значимости 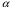 и числе степеней свободы: 1 и и числе степеней свободы: 1 и 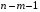 . Если фактическое значение . Если фактическое значение 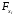 превышает превышает 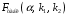 , то дополнительное включение фактора , то дополнительное включение фактора 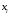 в модель статистически оправданно и коэффициент чистой регрессии в модель статистически оправданно и коэффициент чистой регрессии 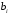 при факторе при факторе 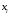 статистически значим. Если же фактическое значение статистически значим. Если же фактическое значение 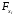 меньше табличного, то дополнительное включение в модель фактора меньше табличного, то дополнительное включение в модель фактора 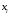 не увеличивает существенно долю объясненной вариации признака не увеличивает существенно долю объясненной вариации признака 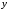 , следовательно, нецелесообразно его включение в модель; коэффициент регрессии при данном факторе в этом случае статистически незначим. , следовательно, нецелесообразно его включение в модель; коэффициент регрессии при данном факторе в этом случае статистически незначим.Для двухфакторного уравнения частные 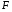 -критерии имеют вид: -критерии имеют вид: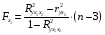 , , 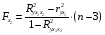 . (2.23а) . (2.23а)С помощью частного 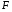 -критерия можно проверить значимость всех коэффициентов регрессии в предположении, что каждый соответствующий фактор -критерия можно проверить значимость всех коэффициентов регрессии в предположении, что каждый соответствующий фактор 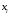 вводился в уравнение множественной регрессии последним. вводился в уравнение множественной регрессии последним.Частный 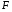 -критерий оценивает значимость коэффициентов чистой регрессии. Зная величину -критерий оценивает значимость коэффициентов чистой регрессии. Зная величину 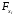 , можно определить и , можно определить и 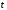 -критерий для коэффициента регрессии при -критерий для коэффициента регрессии при 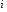 -м факторе, -м факторе, 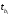 , а именно: , а именно: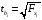 . (2.24) . (2.24)Оценка значимости коэффициентов чистой регрессии по 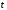 -критерию Стьюдента может быть проведена и без расчета частных -критерию Стьюдента может быть проведена и без расчета частных 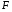 -критериев. В этом случае, как и в парной регрессии, для каждого фактора используется формула: -критериев. В этом случае, как и в парной регрессии, для каждого фактора используется формула: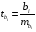 , (2.25) , (2.25)где 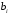 – коэффициент чистой регрессии при факторе – коэффициент чистой регрессии при факторе 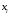 , , 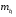 – средняя квадратическая (стандартная) ошибка коэффициента регрессии – средняя квадратическая (стандартная) ошибка коэффициента регрессии 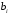 . .Для уравнения множественной регрессии 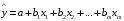 средняя квадратическая ошибка коэффициента регрессии может быть определена по следующей формуле: средняя квадратическая ошибка коэффициента регрессии может быть определена по следующей формуле: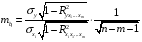 , (2.26) , (2.26)где 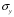 – среднее квадратическое отклонение для признака – среднее квадратическое отклонение для признака 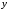 , , 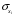 – среднее квадратическое отклонение для признака – среднее квадратическое отклонение для признака 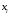 , , 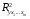 – коэффициент детерминации для уравнения множественной регрессии, – коэффициент детерминации для уравнения множественной регрессии, 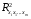 – коэффициент детерминации для зависимости фактора – коэффициент детерминации для зависимости фактора 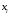 со всеми другими факторами уравнения множественной регрессии; со всеми другими факторами уравнения множественной регрессии; 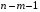 – число степеней свободы для остаточной суммы квадратов отклонений. – число степеней свободы для остаточной суммы квадратов отклонений. |
