|
|
Ответы на билеты. 1. Задачи обеспечения безопасности информации (оби), решаемые стохастическими методами
Недостатки:
Необходимость надёжного канала связи (КС) для обмена ключами (надежного канала нет. Необходимость наличия недоступных для противника секретных каналов для обмена ключами делает подход дорогостоящим и практически неприменимым).
Невозможность разрешения конфликтов: при их возникновении арбитр оказывается в безвыходной ситуации, т.к. секретную ключевую информацию знают как минимум двое участников информационного обмена. А это означает, что в рамках системы невозможно обеспечить юридическую значимость пересылаемых электронных документов.
8. Модель криптосистемы с открытым ключом. Криптосистема RSA.
Идея предложена Диффи и Хеллманом в 1978 г. При шифровании с открытым ключом для зашифрования и расшифрования используются разные ключи и знание одного из них не дает практической возможности определить второй. В результате ключ зашифрования может быть сделан открытым без потери стойкости шифра, и лишь ключ расшифрования держится в секрете.
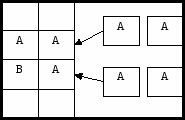 
Активный участник B, он запускает генератор ключевой пары. Оба ключа принадлежат В.
 – секретный (security) ключ абонента B – ключ расшифрования. – секретный (security) ключ абонента B – ключ расшифрования.
 –открытый (public) ключ абонента B – ключ зашифрования. –открытый (public) ключ абонента B – ключ зашифрования.
Ключи: образуют неразрывную пару, два взаимообратных преобразования, один из другого получить нельзя.
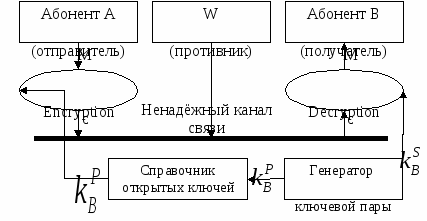
Пользователь В, который хочет получать конфиденциальные сообщения, должен выбрать одностороннюю функцию Ев с секретным ключом КВ. Он сообщает всем заинтересованным описание своей функции зашифрования Ев, например публикует его в справочнике открытых ключей. При этом ключ КВ, а следовательно и алгоритм расшифрования DB, держатся в секрете. Если теперь пользователь А хочет послать В секретное сообщение М, то он находит в справочнике функцию EB, а затем вычисляет С = ЕВ(М) и посылает шифротекст С по открытому каналу пользователю В. Последний, зная КВ, т.е. умея инвертировать ЕВ, определяет М по полученному С, вычисляя М = DB(С). Противник, не зная ключа, в силу второго свойства односторонней функции с секретом не сможет прочитать секретную информацию. В отличие от криптосистемы в секретным ключом, если абонент А, зашифровав сообщение М для В, сохранит С, но потеряет М или забудет его содержание, он не будет иметь никаких преимуществ перед противником в раскрытии исходного М из С.
«+»: Юридическая значимость, т.к. только один участник знает секретную информацию (ключ).
«–»: 1. Справочник открытых ключей хранит все открытые ключи всех абонентов.
Проблема: подлинность открытых ключей, взятых из справочника. Нет гарантий, что его не подменили ( и и  формирует противник). 2. Низкое быстродействие. 3. Возможна атака с проверкой текста, т.е. если число открытых текстов невелико, противник, зная открытый ключ, может заранее заготовить соответствующие ему шифротексты, а затем, сравнивая с ними перехваченные шифровки, получать соответствующие последним открытые тексты. формирует противник). 2. Низкое быстродействие. 3. Возможна атака с проверкой текста, т.е. если число открытых текстов невелико, противник, зная открытый ключ, может заранее заготовить соответствующие ему шифротексты, а затем, сравнивая с ними перехваченные шифровки, получать соответствующие последним открытые тексты.
Примеры систем с открытым ключом: ранцевая криптосистема, RSA, криптосистема, основанная на свойствах эллиптических кривых.
Криптосистема с открытым ключом RSA
Первая криптосистема с ОК. Она основана на том факте, что легко перемножить два больших простых числа, в то же время крайне трудно разложить на множители их произведение. В результате их произведение может быть использовано в качестве открытого ключа зашифрования.
Построение криптосистемы RSA.
Выберем p, q – простые большие различные числа. Для примера возьмем p = 3 и q = 11.
Перемножаем 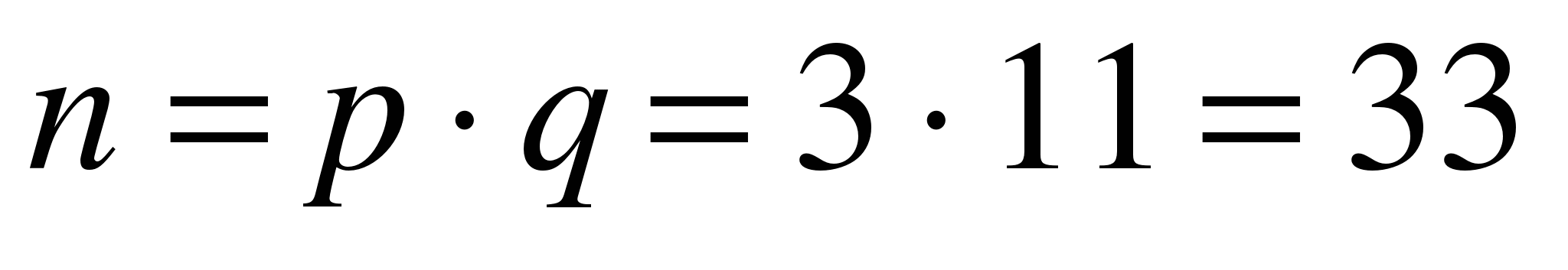
Функция Эйлера 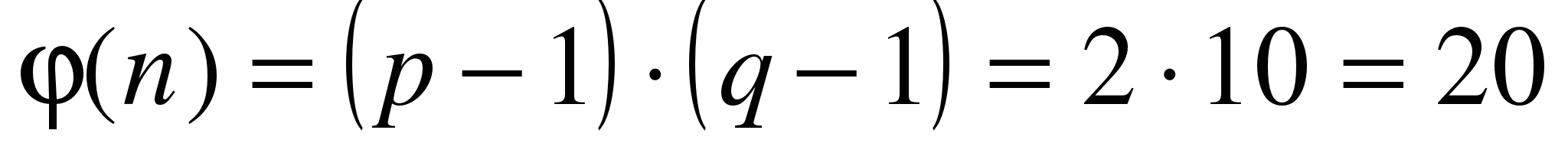
Найти 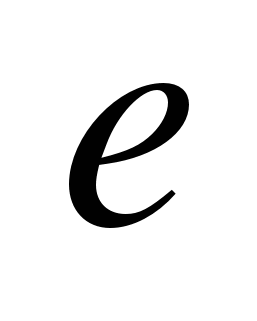 , взаимно простое к , взаимно простое к  : : 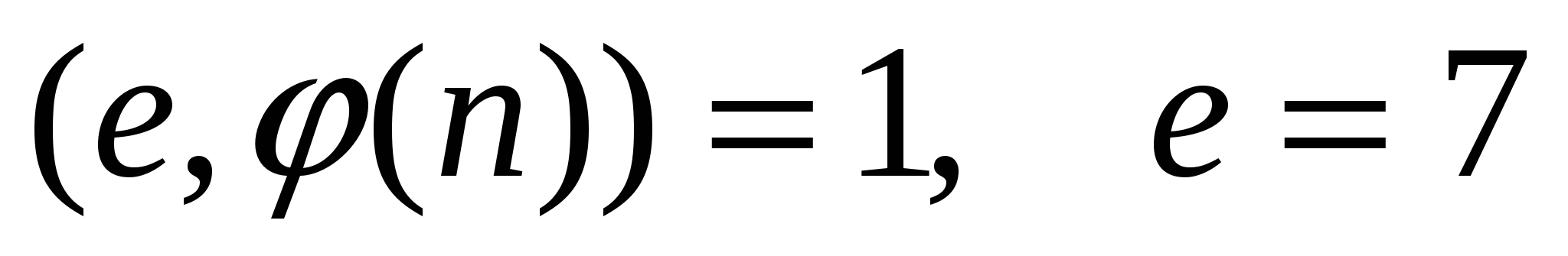
Найти число 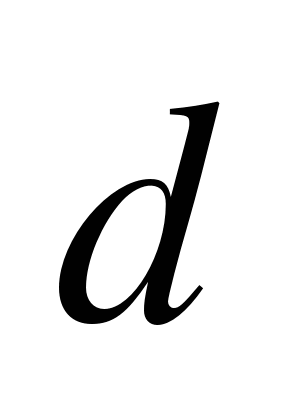 , такое что , такое что 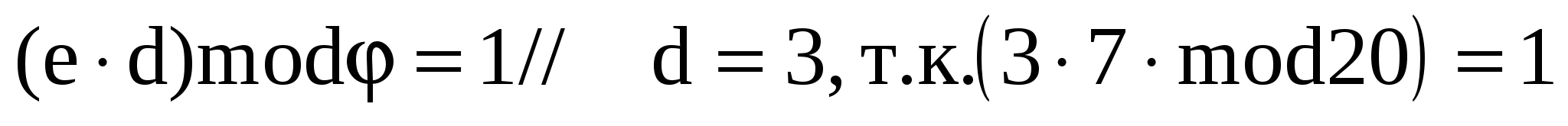
p и q уничтожаем
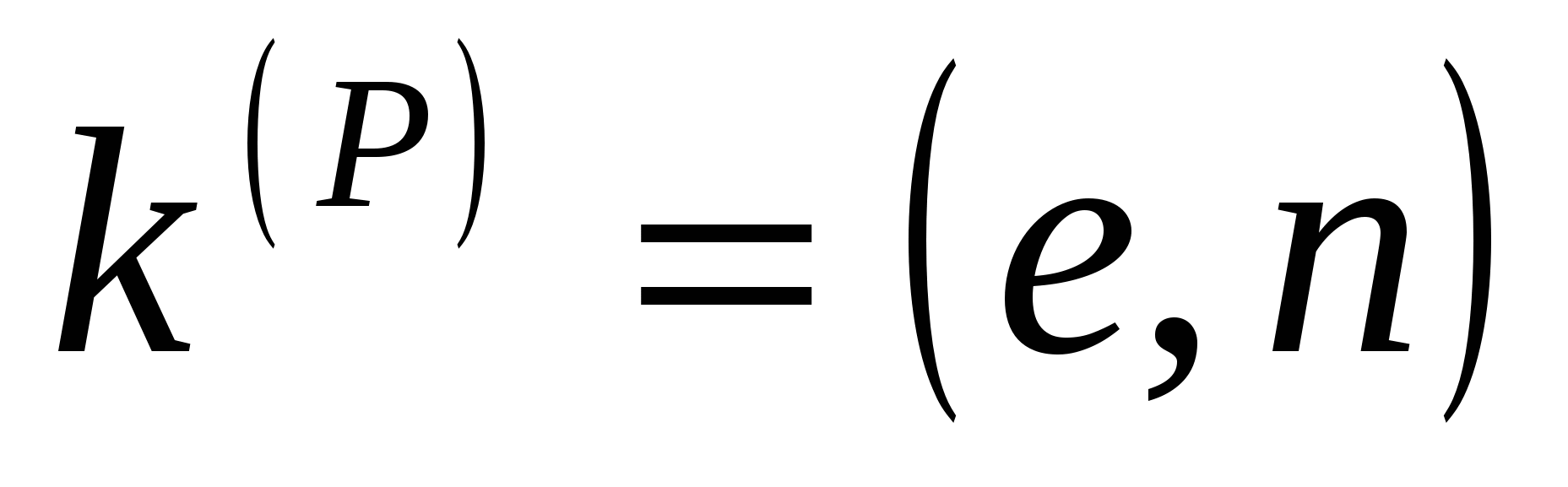 – ключ зашифрования (открытый ключ) – ключ зашифрования (открытый ключ)
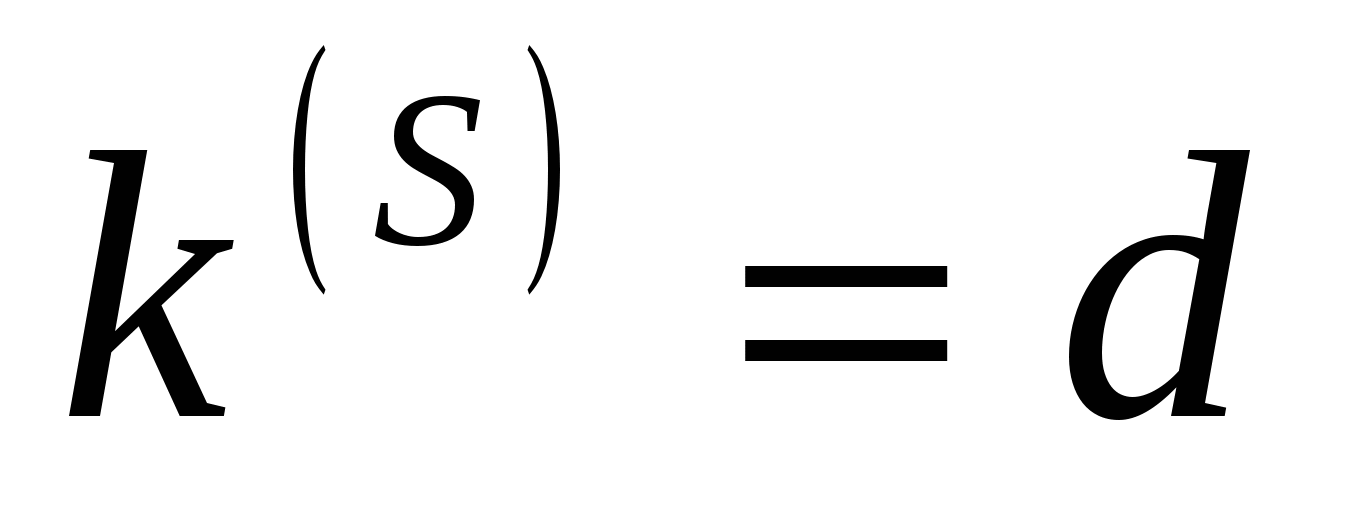 – ключ расшифрования (секретный ключ) – ключ расшифрования (секретный ключ)
Если 1-5 верны, то 
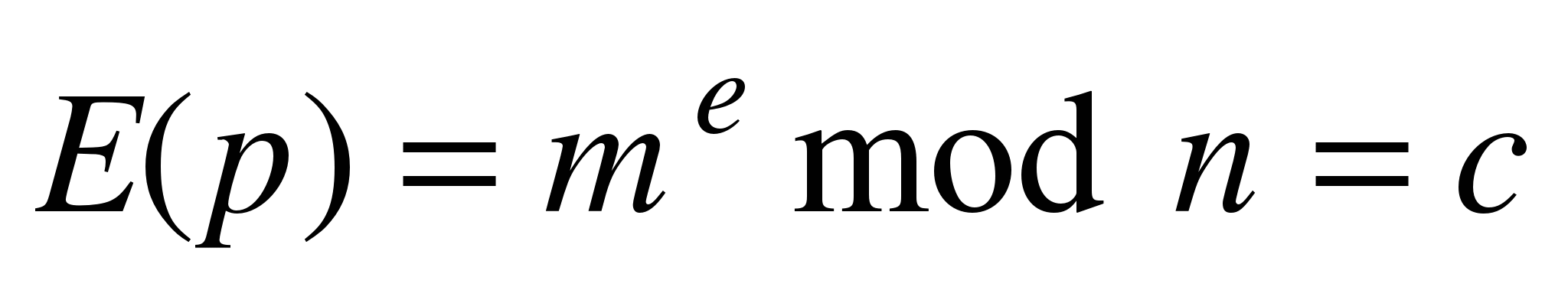 – зашифрование – зашифрование
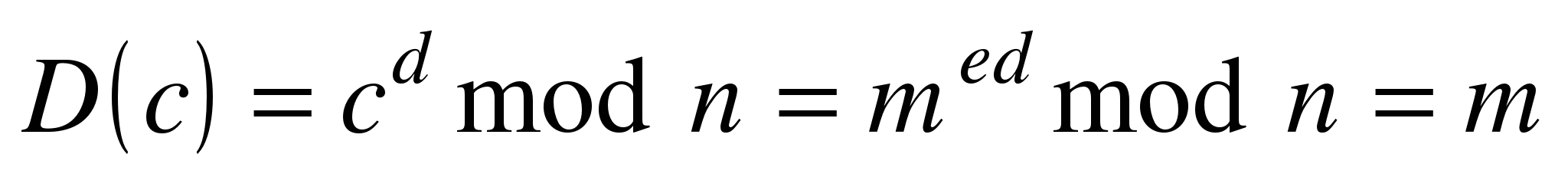 – расшифрование – расшифрование
E и D взаимообратные: 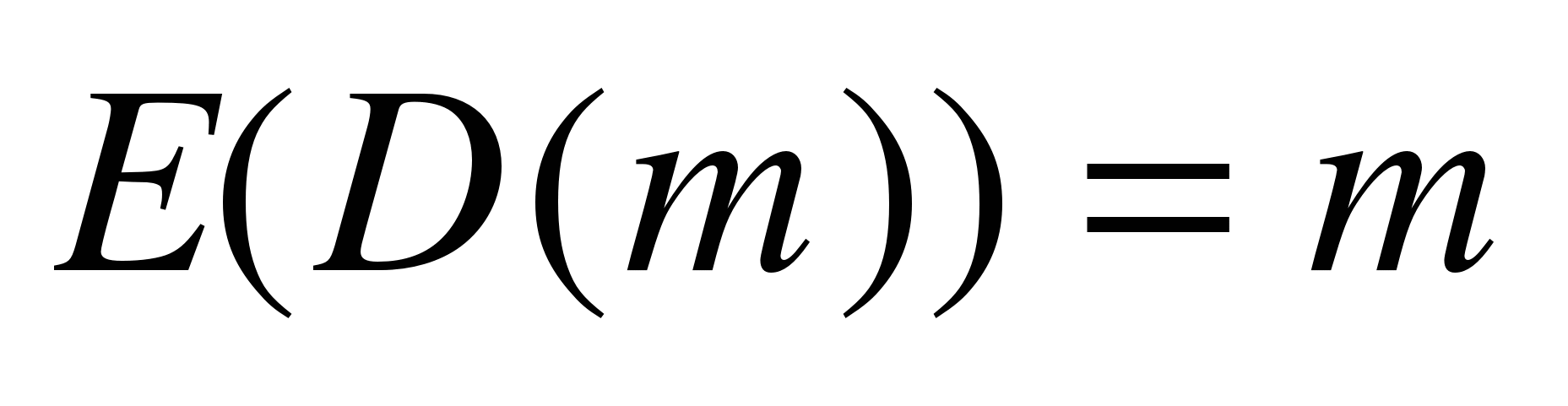 и и 
Взлом этого шифра – разложение числа 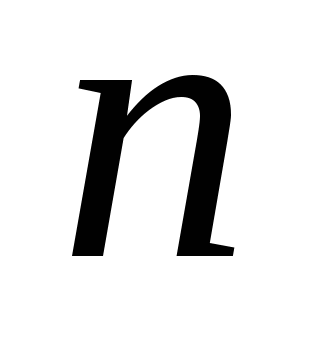 на простые сомножители на простые сомножители 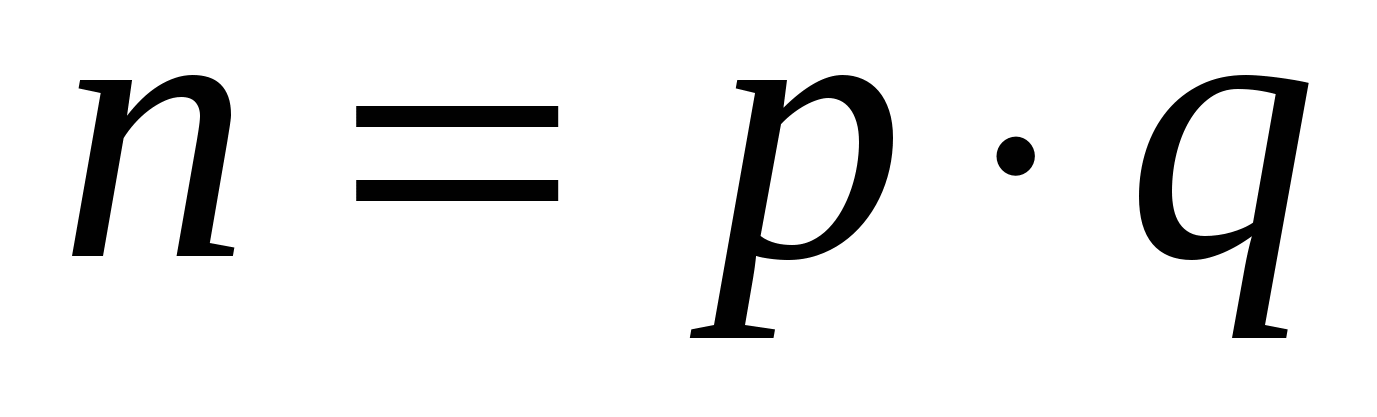
9. Протокол выработки общего секретного ключа
Диффи и Хеллман предложили протокол выработки общего секретного ключа, т.е. процедуру взаимодействия по открытому каналу связи удаленных абонентов А и В, обладающую следующими свойствами:
в конце процедуры у А и В появляется общая секретная информация (общий секретный ключ), которой до начала действия протокола не было.
Противник, который способен перехватывать все сообщения и знает цель протокола, не может восстановить сформированный секретный ключ.
Протокол основывается на задаче дискретного логарифмирования. Противник, который хочет узнать формулируемый секретный ключ, вынужден решать именно эту трудную математическую задачу. Пусть р – большое простое число, ɷ – примитивный элемент поля GF(p). Числа р и ɷ считаются общедоступными. Тогда процедуры получения информации имеет следующий вид:
Функция 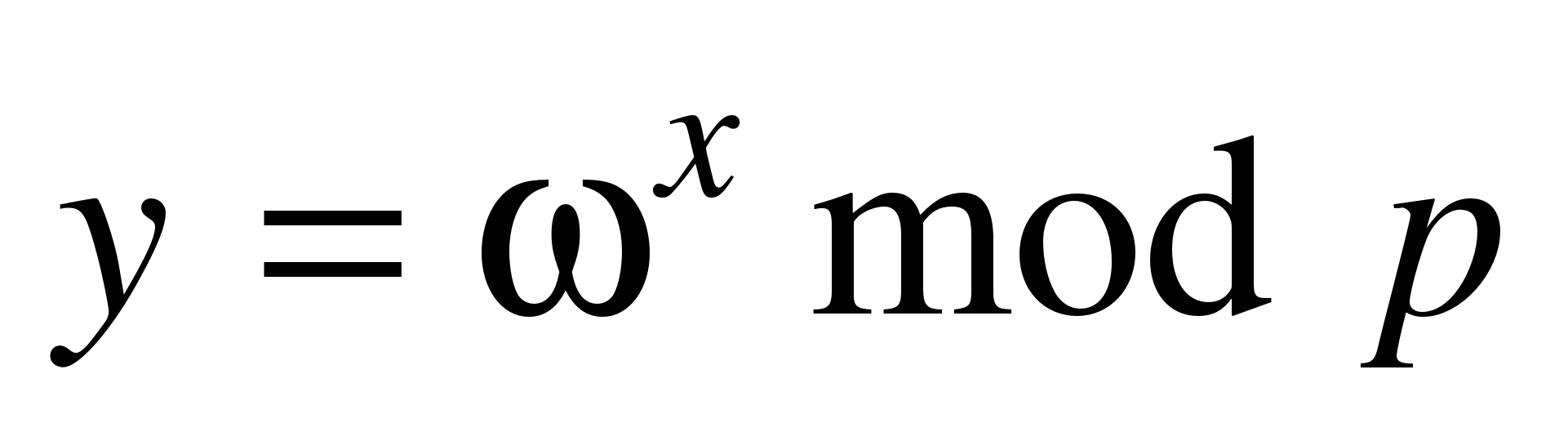 – главный кандидат на звание односторонней. Обратная задача – дискретное логарифмирование (вычислительно неразрешима). – главный кандидат на звание односторонней. Обратная задача – дискретное логарифмирование (вычислительно неразрешима).
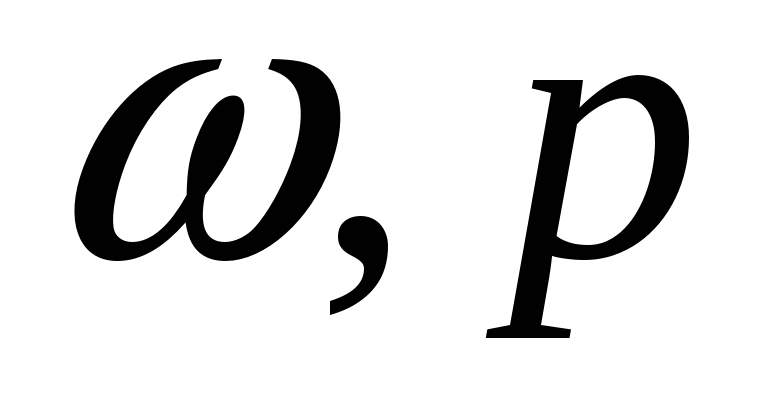 – открытые параметры, известны всем. – открытые параметры, известны всем.
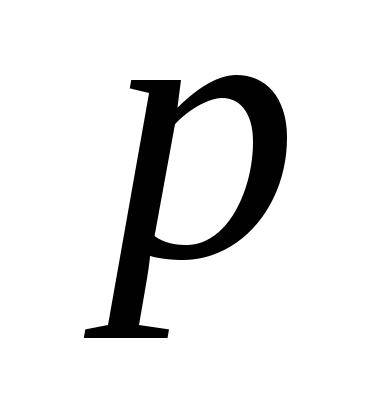 – очень большое простое число (несколько десятков десятичных знаков). – очень большое простое число (несколько десятков десятичных знаков).
 – обычное большое число в первом приближении. Это примитивный элемент конечного поля. – обычное большое число в первом приближении. Это примитивный элемент конечного поля.
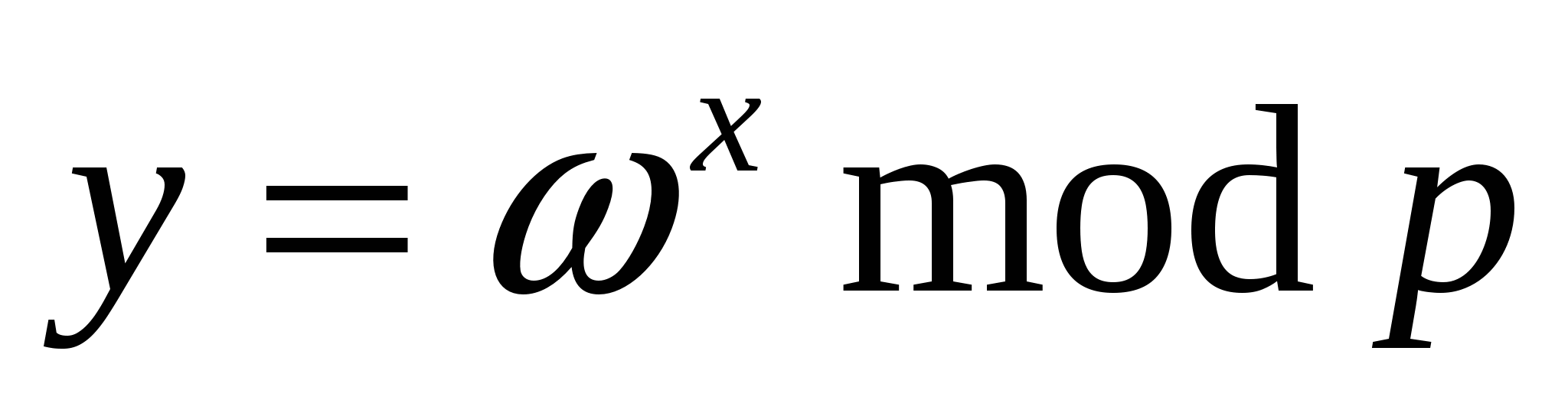

Протокол – интерактивный обмен данными (двусторонний).
Жестко заданный порядок обмена сообщениями
Жестко заданы, стандартизированы форматы пересылаемых сообщений
Реакция на сбой при реализации протокола (fault attacks)
Цель протокола: в конце протокола, т.е. обмена между А и В по открытому каналу связи, у обоих абонентов будет общая секретная информация (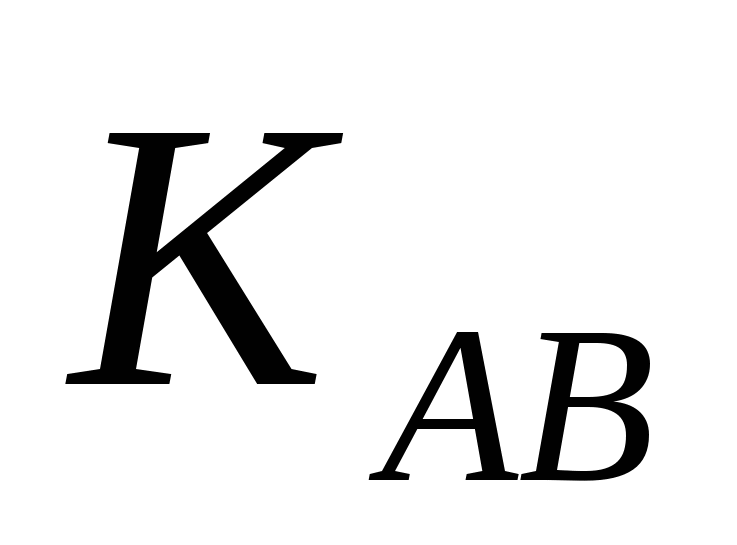 ) )
Протокол стохастический (используется генерация псевдослучайных чисел).
Абонент А вырабатывает большое случайное число (секретный ключ xA) затем формирует и передает абоненту B сообщение 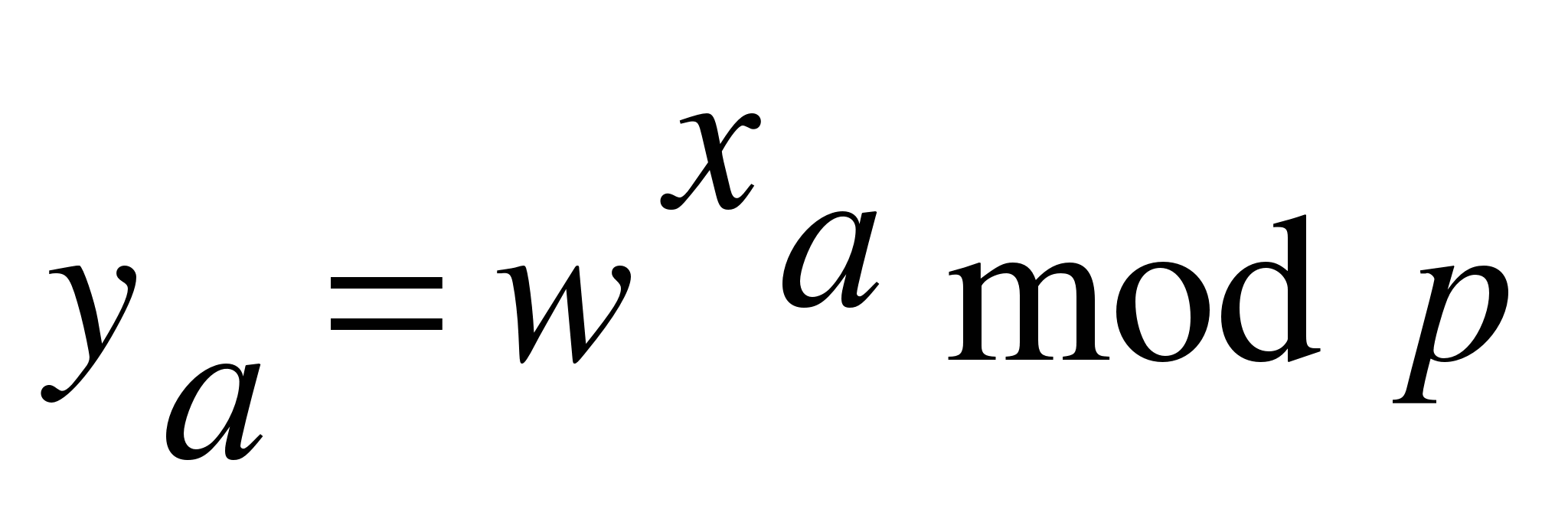
Абонент B запускает свой ГПСП и вырабатывает случайное секретное число (xB), формирует и передает абоненту А сообщение 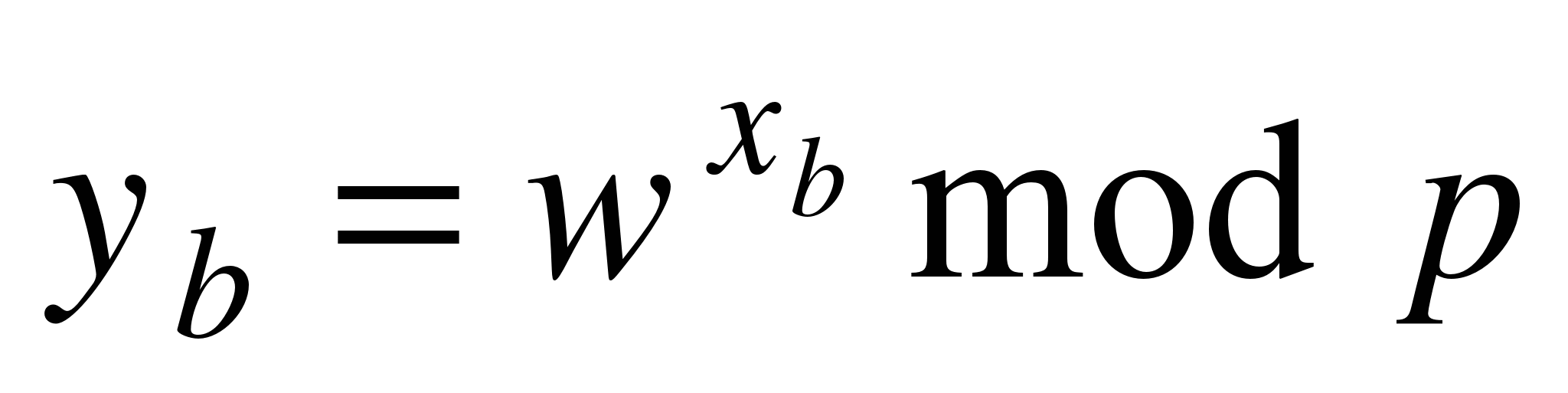 . .
Пример: 15 mod 7 = 1
Абонент А выполняет операцию 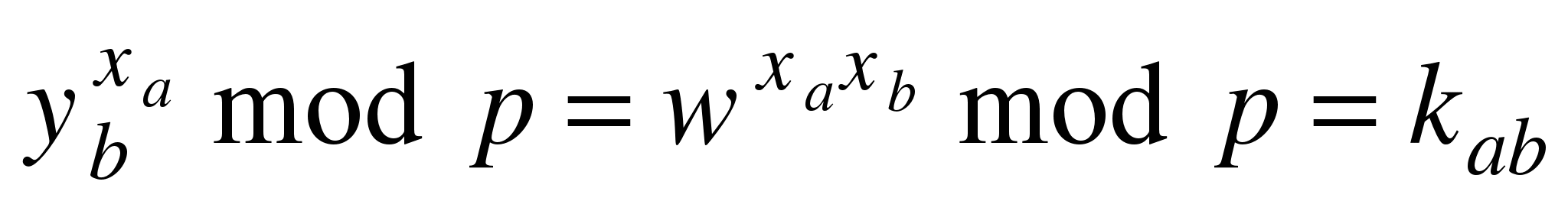 . Это число абонент А объявляет общим секретном ключом. . Это число абонент А объявляет общим секретном ключом.
Абонент B: 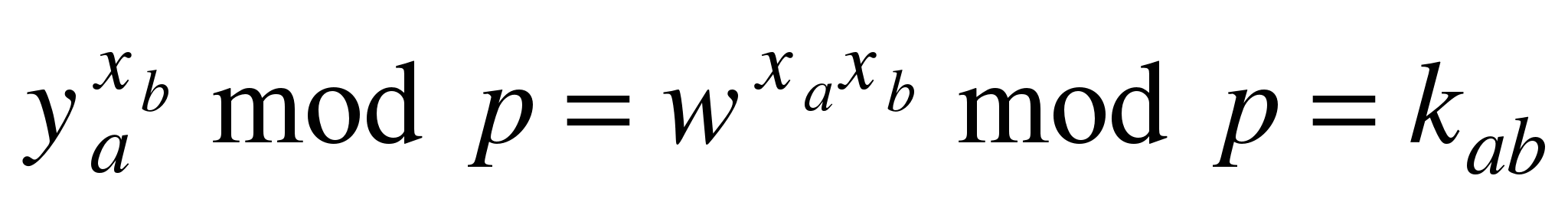
Стойкость протокола обеспечивается односторонней функцией и качественным ГПСП.
10. Протокол электронной цифровой подписи (ЭЦП)
Протоколы или схемы ЭЦП являются основным криптографическим средством обеспечения аутентичности информации:
С помощью ЭЦП получатель документа может доказать, что он принадлежит отправителю, при этом автор подписи не сможет оспорить факт отправления подписанного документа.
ЭЦП невозможно подделать, только абонент, чья подпись стоит на документе, мог подписать данный документ.
ЭП является неотъемлемой частью документа, перенести ее на другой документ нельзя.
Ни противник, ни получатель не могут изменить документ, оставив данный факт незамеченным.
Любой пользователь, имеющий образец подписи, может удостовериться в подлинности документа.
Схема ЭП включает в себя:
Параметр безопасности, в качестве которого может выступать длина подписи, длина подписываемых сообщений.
Пространство исходных сообщений.
Максимальное число подписей, которые могут быть получены в данной схеме без замены секретного ключа.
Алгоритм генерации ключей – полиномиальный вероятностный алгоритм, формирующий по заданному n пару: ksecret, секретный ключ подписывающего абонента, и kpublic, соответствующий открытый ключ проверяющего абонента.
Алгоритм S формирования подписи сообщения – полиномиальный вероятностный алгоритм, вырабатывающий по заданному исходному сообщению М и секретному ключу ksecret подпись s для сообщения М.
Алгоритм проверки V подписи – полиномиальный вероятностный алгоритм, дающий на выходе при заданных сообщении М, открытом ключе kpublic и возможной подписи s’ либо значение 1, когда подпись принимается, либо 0, когда подпись отвергается.
СРАВНЕНИЕ РУКОПИСНОЙ И ЭЛЕКТРОННО-ЦИФРОВОЙ ПОДПИСЕЙ
Параметры
|
ЭЦП
|
Рукописная
|
Возможность подделки
|
Да
|
Да
|
Квалификация нарушителя
|
Очень высокая (криптоанализ)
|
Средняя
|
Кто может обнаружить (доказать) факт подделки
|
Криптограф
|
Графолог
|
Возможность раздельного существования
подписи и документа
|
Да
|
Нет
|
Возможность копирования
подписанного документа
|
Да
|
Нет
|
Подпись s = S K(secret)(M) называется допустимой для сообщения М, если она принимается алгоритмом V с вероятностью, близкой к 1. Подделкой подписи сообщения М называется нахождение противником, не имеющим секретного ключа подписывающего, допустимой подписи для этого сообщения.
Идея электронной цифровой подписи
E A, EB – открытые ключи A, EB – открытые ключи
DA, DB – секретные ключи
Необходимо обеспечить аутентичность (целостность, подлинность и т.д.):
а) объекта информационного взаимодействия (сообщения или массива данных) – целостность и подлинность
б) субъекта ИВ (абонентов) – только подлинность
Подпись нужна для доказательства подлинности пересылаемого документа, для обеспечения секретности, аутентичности и доступности пересылаемого документа.
2 варианта отправки:
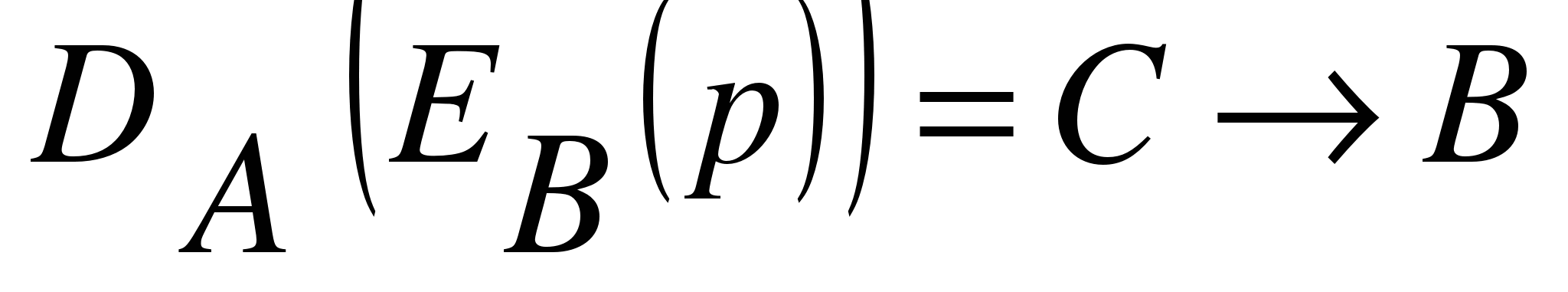
Документ 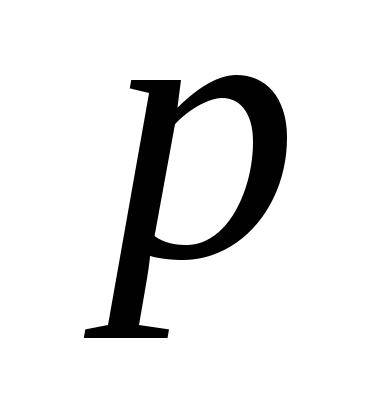 преобразуется на алгоритме преобразуется на алгоритме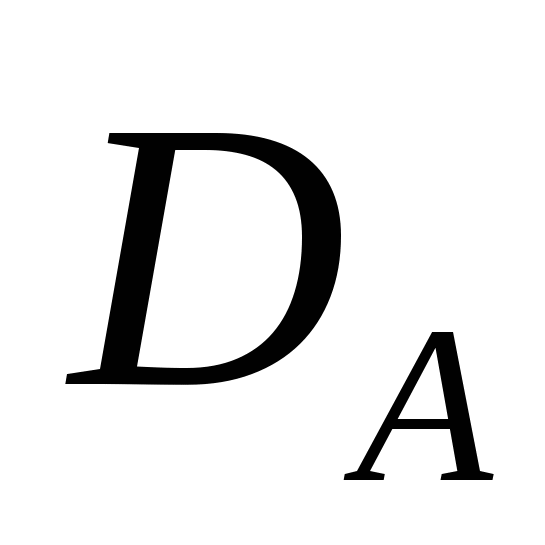 , полученная информация преобразуется на , полученная информация преобразуется на 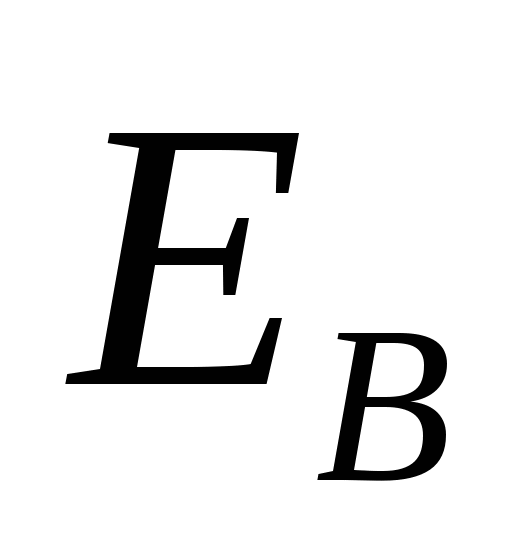 → C. → C.
С отсылается абоненту В и он расшифровывает: 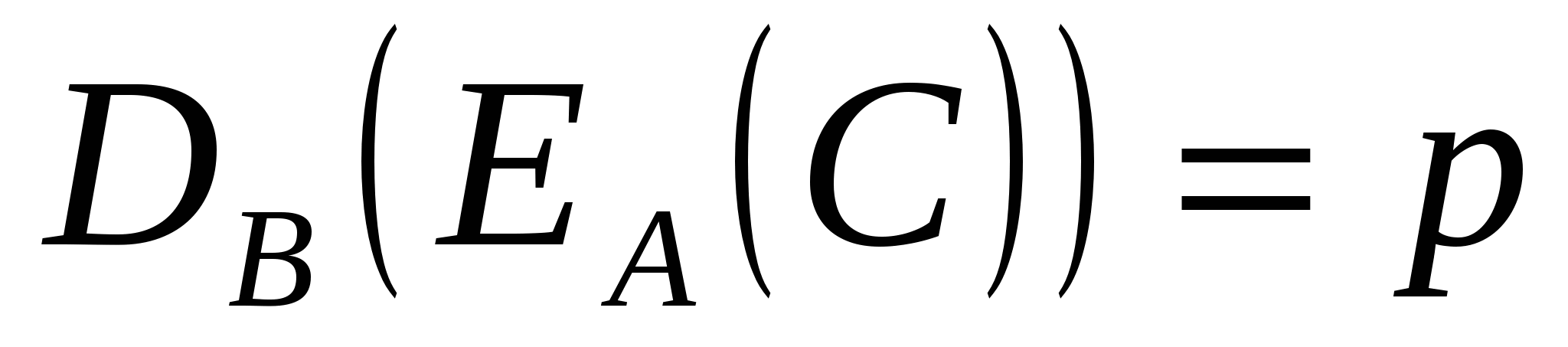 . Получив р, В понимает что документ от А (с его ЭЦП). НЕ ВЕРНО! Т.к. W может снять действие А своим ключом и поставить свою ЭЦП. . Получив р, В понимает что документ от А (с его ЭЦП). НЕ ВЕРНО! Т.к. W может снять действие А своим ключом и поставить свою ЭЦП.
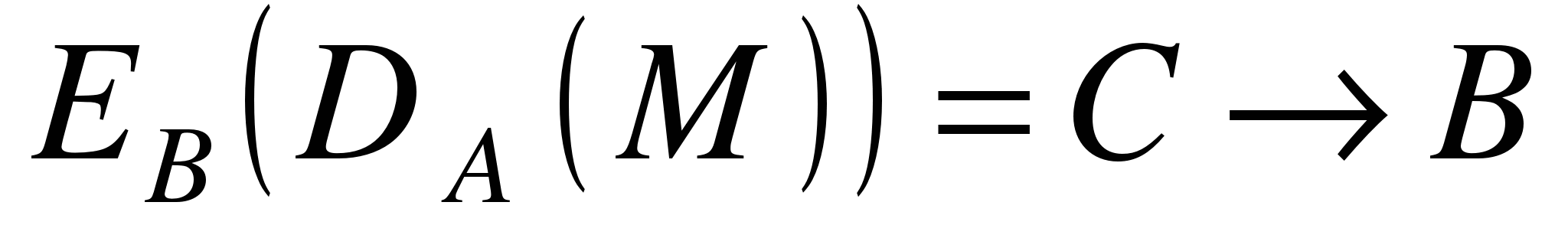 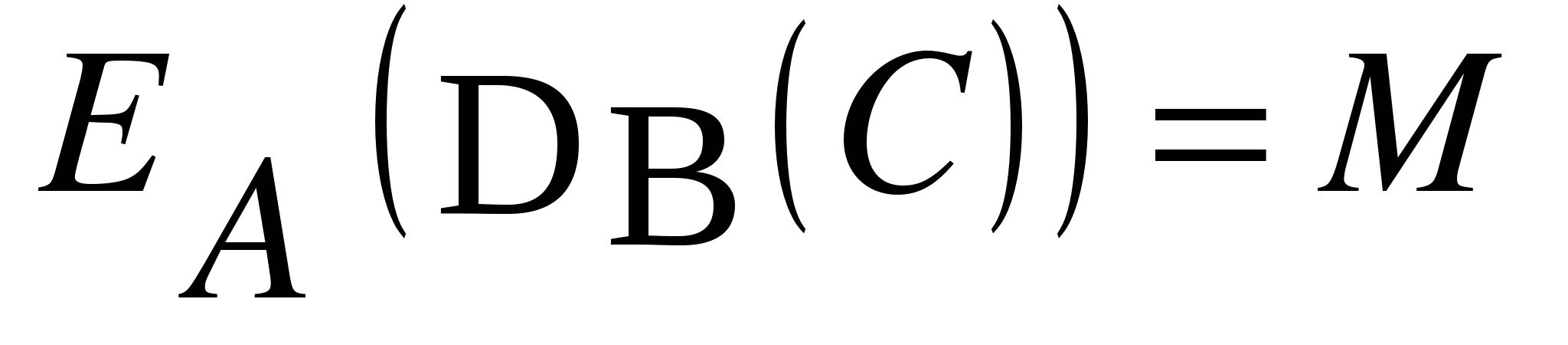 Недостаток: очень низкое быстродействие, поэтому редко применяется. Недостаток: очень низкое быстродействие, поэтому редко применяется.
Классическая схема электронной цифровой подписи.
 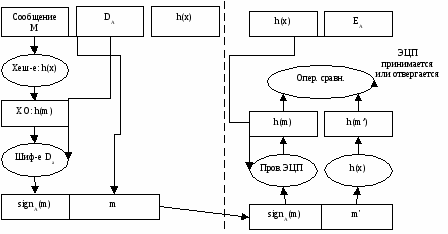 – формирует подпись; – формирует подпись;
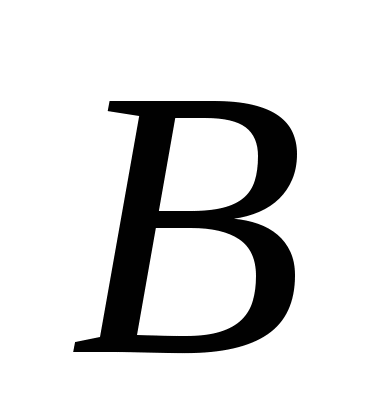 – проверяет подпись; – проверяет подпись;
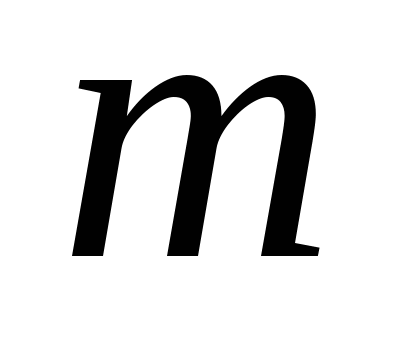 – электронный документ (message), который необходимо подписать; – электронный документ (message), который необходимо подписать;
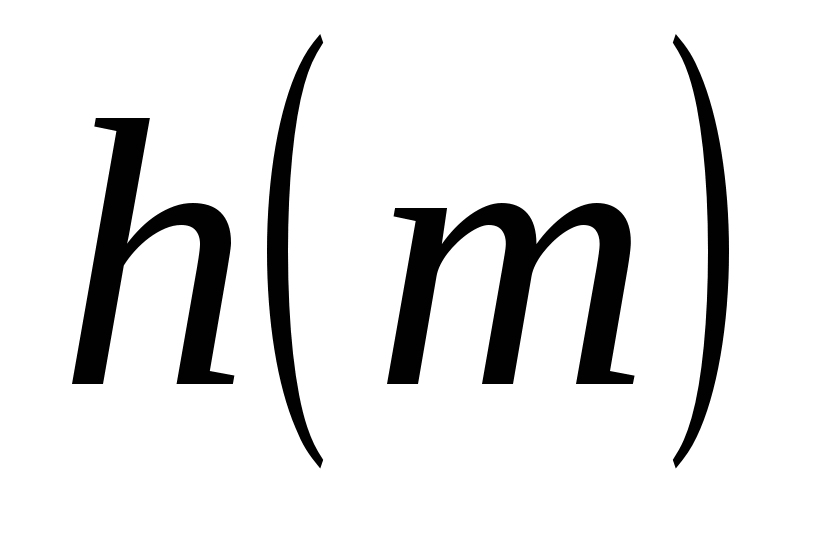 – хеш-образ ЭД; – хеш-образ ЭД;
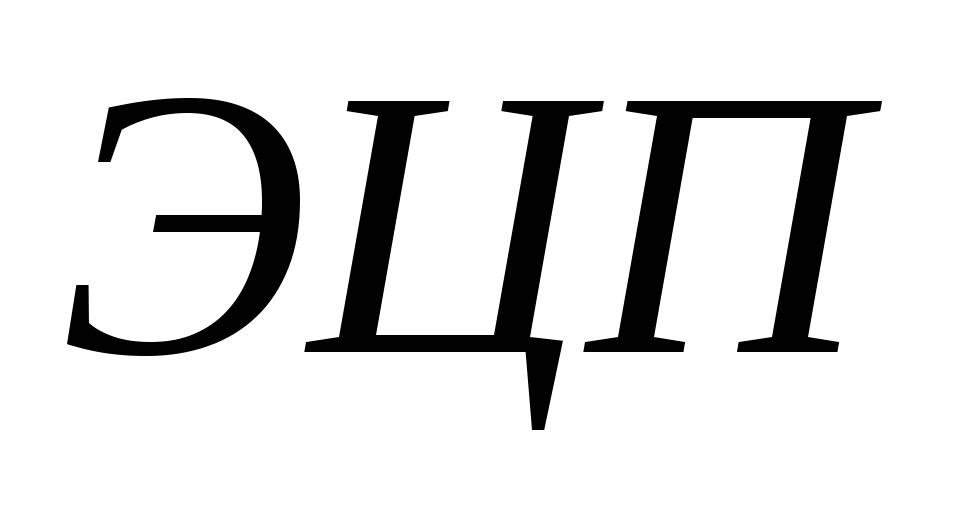 – формирование ЭЦП; – формирование ЭЦП;
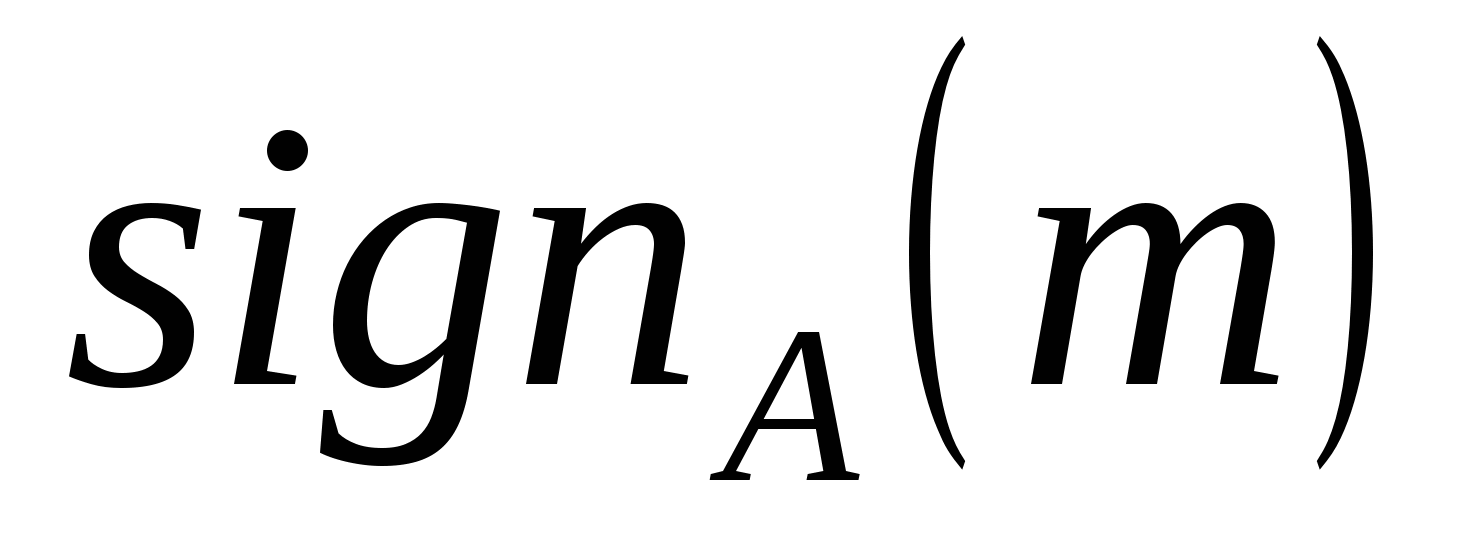 = Da(h(M)) – сигнатуры; = Da(h(M)) – сигнатуры;
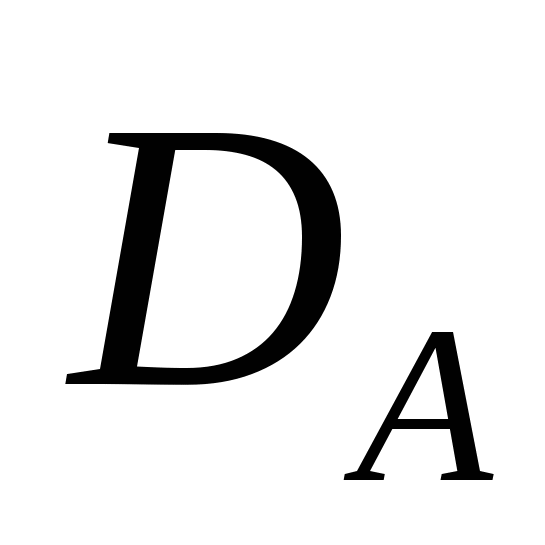 – секретный ключ абонента – секретный ключ абонента 
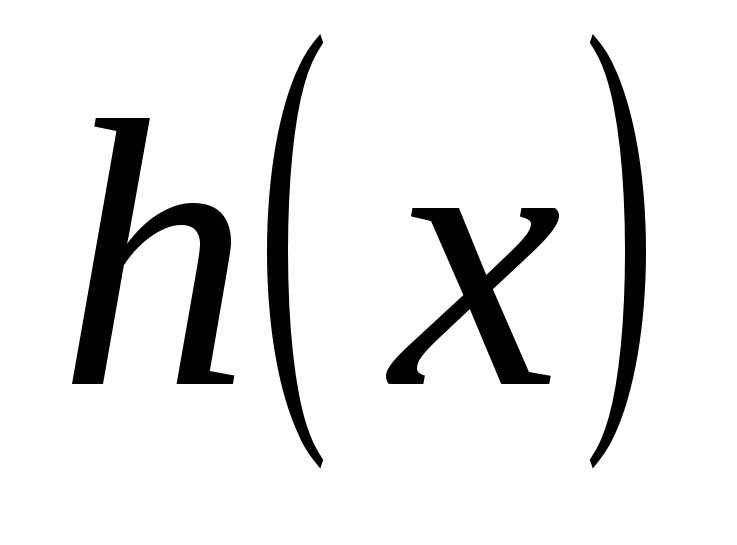 – общедоступная функция сжатия (хэш-функция) – общедоступная функция сжатия (хэш-функция)
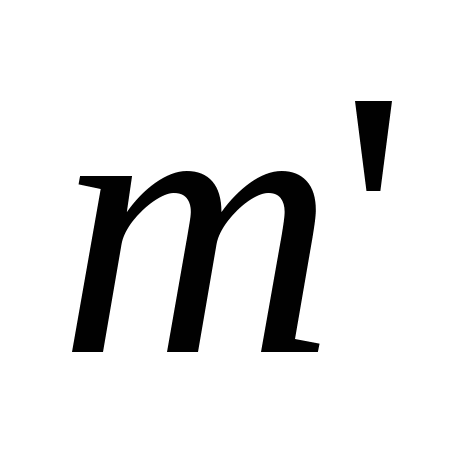 – возможно искаженный ЭД – возможно искаженный ЭД 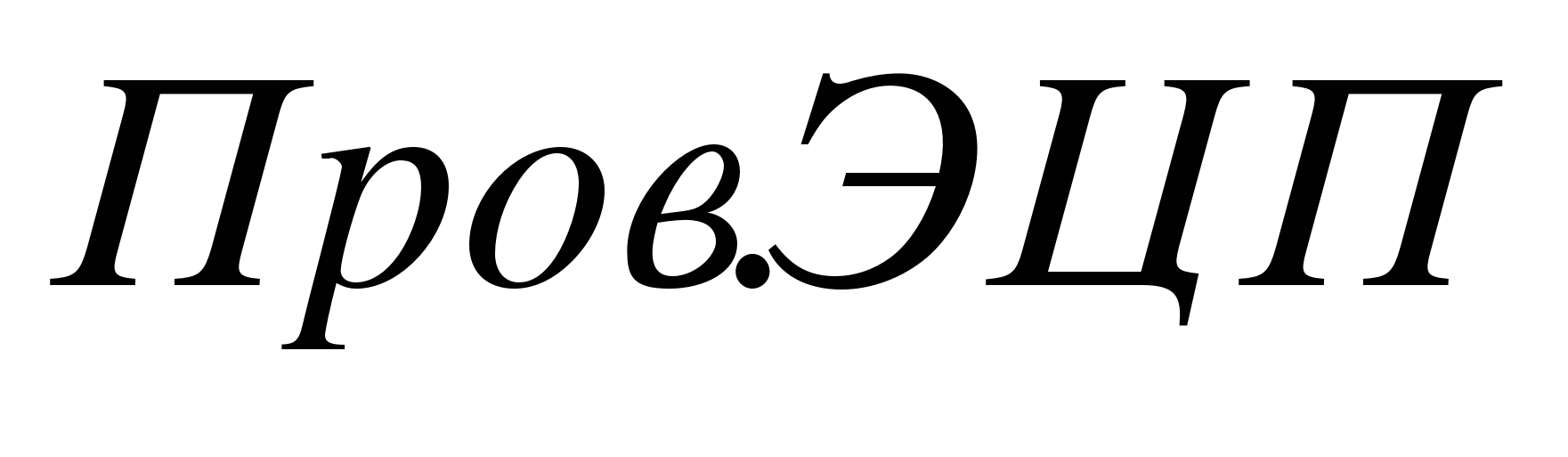 – проверка ЭЦП – проверка ЭЦП
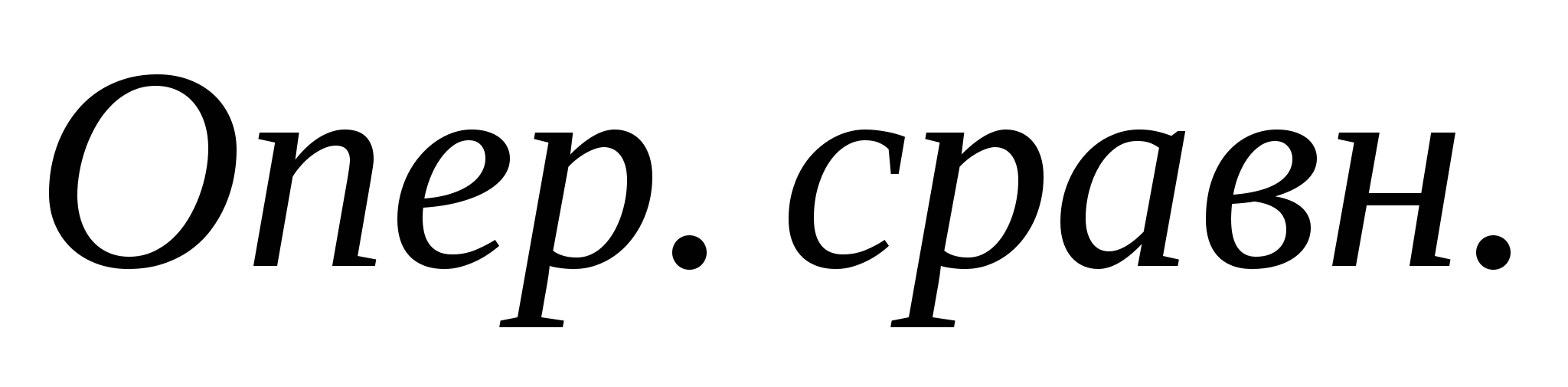 – операция сравнения, по ЭЦП определяет, принимать или отвергать сообщения – операция сравнения, по ЭЦП определяет, принимать или отвергать сообщения
Отправитель А вычисляет (ksecret, kpublic) = G(n) и посылает kpublic получателю В, сохраняя ksecret в секрете.
Для получения подписи документа М отправитель А вычисляет s = S K(secret)(M) и посылает М и s получателю В.
Получатель вычисляет V(M, s, ka(public)) и в зависимости от результата принимает или отвергает подпись s и сообщение М.
В классической схеме ЭП предполагается, что подписывающий знает содержание документа М, который он подписывает. Проверяющий, зная открытый ключ проверки подписи, может проверить правильность подписи в любое время без какого-либо разрешения или участия А. При создании ЭП по классической схеме претендент А выполняет следующую последовательность действий:
Применяет к исходному сообщению М ХФ и формирует хеш-образ сообщения h(M).
При необходимости дополняет хеш-образ до требуемой длины (ext).
Вычисляет ЭП s с использованием несимметричного криптоалгоритма Dk и секретного ключа создания подписи: s = Da(secret)(Ext(h(M))).
ХФ является неотъемлемой частью схем ЭП. Применение медленных несимметричных криптоалгоритмов для преобразования всего исходного сообщения М нерационально, поэтому для повышения быстродействия схемы перед процедурой формирования подписи используется функция необратимого сжатия информации.
Абонент В, получив сообщение:
Применяет к тексту полученного сообщения ХФ.
Дополняет в случае необходимости хеш-образ до требуемой длины.
Применяет к полученной подписи s несимметричный криптоалгоритм Ek с использованием открытого ключа проверки подписи и сравнивает полученное значение Ea(public)(s) с найденным на предыдущем шаге. При положительном результате сравнения подпись признается, при отрицательном – отвергается.
|
|
|
 Скачать 2.35 Mb.
Скачать 2.35 Mb.


 A, EB – открытые ключи
A, EB – открытые ключи – формирует подпись;
– формирует подпись;