|
|
Ответы на билеты. 1. Задачи обеспечения безопасности информации (оби), решаемые стохастическими методами
1. Задачи обеспечения безопасности информации (ОБИ), решаемые стохастическими методами
Цель создания систем безопасности – предупреждение, устранение последствий умышленного и случайного деструктивного воздействия, следствием которого может быть разрушение, модификация, утечка информации и дезинформирование.
Обеспечение секретности (конфиденциальности) информации
Обеспечение аутентичности объектов и субъектов информационного взаимодействия
Защита прав собственника информации
Обеспечение юридической значимости электронных документов
Обеспечение устойчивости к разрушающим программным воздействиям (РПВ)
Обеспечение неотслеживаемости информации
Правильность функционирования всех компонентов системы в любое время.
Своевременный доступ пользователей к необходимой им информации.
Контроль правильности реализации алгоритма управления.
Непрерывный анализ защищенности процессов передачи, обработки информации.
Должны проверить, что источник информации тот, за кого себя выдает.
Должны защитить информацию от атак.
Проверить, что полученное сообщение соответствует отправленному.
Исключить из процесса незаконных участников.
С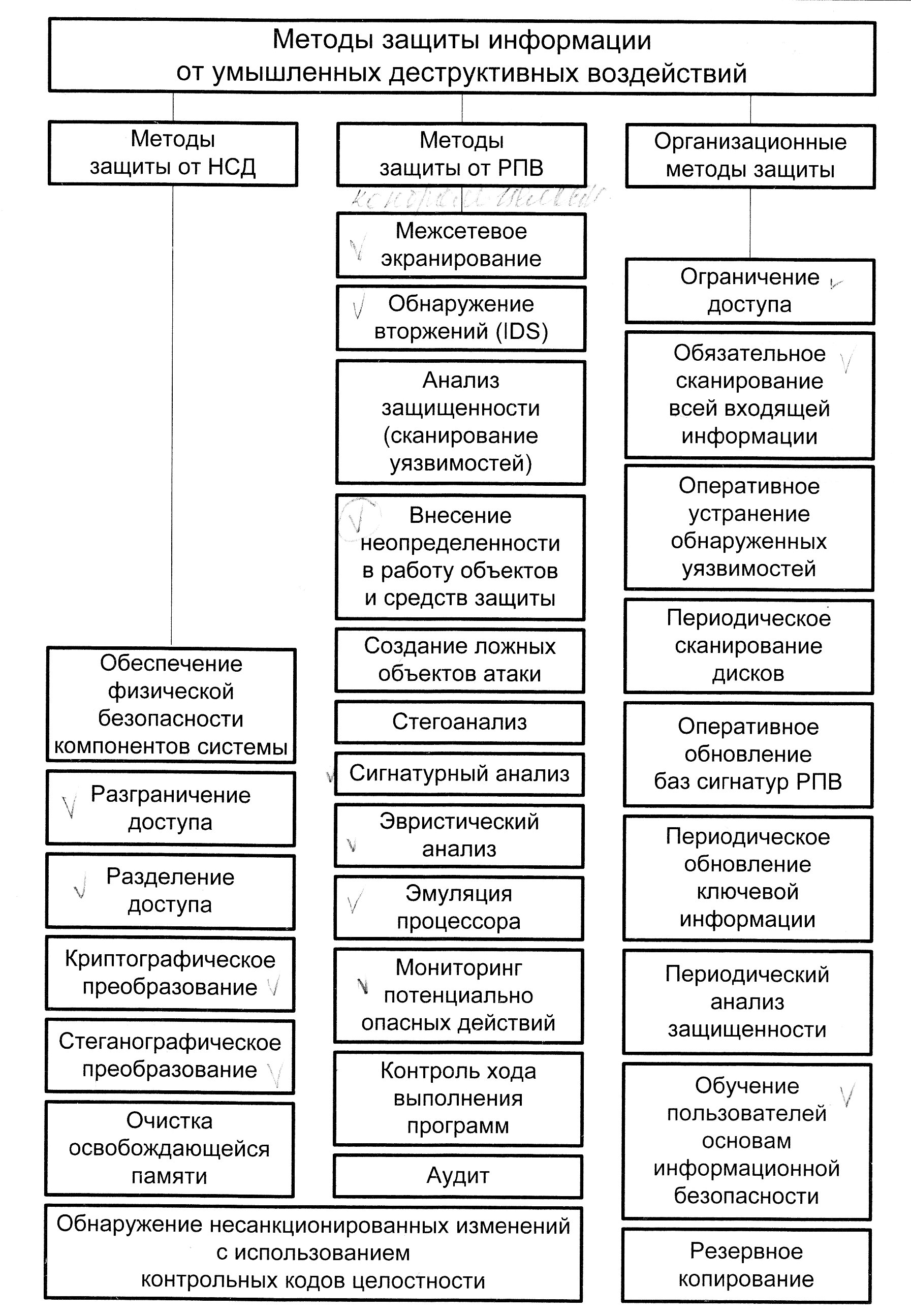 тохастическими методами защиты в широком смысле принято называть методы защиты компьютерных систем, прямо или косвенно основанные на использовании ГПСП и хеш-генераторов (ХГ), при этом эффективность защиты зависит от качества используемых алгоритмов генерации ПСП и алгоритмов хеширования.
ГПСП и ХГ успешно решают почти все задачи ОБИ. При реализации большинства методов защиты используют ГПСП и ХГ. Иначе говоря, эти методы являются стохастическими.
Три группы методов защиты:
1. Защита от случайных воздействий (помехоустойчивое кодирование, самоконтроль, процедуры контроля исправности).
2. Методы защиты информации от умышленных деструктивных воздействий: (см. таблицу).
3. Законодательная защита, принципы работы с системой, снижающие риски нарушения информационной безопасности.
2. Функции генераторов псевдослучайных чисел (ГПСЧ) в системах ОБИ
Стохастическими методами защиты в широком смысле принято называть методы защиты компьютерных систем, прямо или косвенно основанные на использовании ГПСП и хеш-генераторов (ХГ), при этом эффективность защиты зависит от качества используемых алгоритмов генерации ПСП и алгоритмов хеширования.
ГПСП и ХГ успешно решают почти все задачи ОБИ. При реализации большинства методов защиты используют ГПСП и ХГ. Иначе говоря, эти методы являются стохастическими.
Формирование гаммы при шифровании информации в режиме гаммирования.
Формирование ключей и паролей пользователей
Формирование случайных запросов при аутентификации удаленных абонентов по принципу вопрос-ответ.
Формирование случайных чисел в протоколе BOCK (выработки общего секретного ключа)
Формирование затемняющего множителя при слепом шифровании.
Формирование прекурсоров для защиты прав собственников информации.
Формирование элементов вероятностного пространства при внесении неопределенности в результат работы алгоритмов защиты информации, в механизм работы программных средств.
Формирование тестовых воздействий на входы проверяемых компонентов системы при автономном или встроенном диагностировании.
Реализация счетчиков команд и/или адреса компьютерных систем.
Задание последовательности выполнения при внесении неопределенности в последовательность выполнения отдельных шагов алгоритма.
Задание длительности выполнения при внесении неопределенности в длительность выполнения отдельных шагов алгоритма для защиты от утечки по побочным каналам.
3. Функции хеш-генераторов в системах ОБИ
Стохастическими методами защиты в широком смысле принято называть методы защиты компьютерных систем, прямо или косвенно основанные на использовании ГПСП и хеш-генераторов (ХГ), при этом эффективность защиты зависит от качества используемых алгоритмов генерации ПСП и алгоритмов хеширования.
ГПСП и ХГ успешно решают почти все задачи ОБИ. При реализации большинства методов защиты используют ГПСП и ХГ. Иначе говоря, эти методы являются стохастическими.
Необратимое сжатие информации, т.е. преобразование документа в документ фиксированной длины (необратимое сжатие в протоколе ЭП для увеличения его быстродействия)
Необратимое преобразование паролей для защиты парольных систем разграничения доступа.
Формирование контрольных кодов целостности информации или правильности выполнения шагов алгоритма.
Необратимое преобразование случайных запросов при аутентификации по принципу запрос-ответ.
Необратимое преобразование информации для защиты от утечки.
Необратимое преобразование информации с целью защиты прав ее владельца.
Необратимое преобразование информации при реализации метода внесения неопределенности в результат работы криптоалгоритмов.
4. Требования к качественной хеш-функции
Хеш-функцией называется преобразование h, превращающее информационную последовательность М произвольной длины в информационную последовательность фиксированной длины h(M). Процесс получения хеш-функции можно рассматривать как наложение ПСП на входную преобразуемую последовательность.
К хеш-функции предъявляются следующие требования:
Результат работы ХФ должен зависеть от всех двоичных символов исходного сообщения, а также от их взаимного расположения.
ХФ должны быть чувствительна к любым изменениям входной информационной последовательности, при любых изменениях на входе результат действия ХФ должен быть непредсказуем – в среднем должна измениться половина хеш-образа.
Для качественной ХФ следующие три задачи должны быть вычислительно неразрешимы:
Нахождение прообраза. Задача нахождения последовательности М по заданному хеш-образу, т.е. функция должна быть стойкой в плане обращения.
Нахождение коллизии. Задача нахождения последовательностей М и М’, причем М≠М’, таких, что h(M)=h(M’), т.е. ХФ должна быть стойкой в смысле нахождения коллизий.
(Коллизия – два различных массива данных, у которых хеш-образы совпадают).
Нахождение второго прообраза. Задача нахождения для заданной последовательности М другой последовательности M’, M≠M’, такой, что h(M)=h(M’). Отличие от п. 2 заключается в том, что M уже известно.
Самые известные ХФ: MD5, SHA, TIGER, Whirlpool.
5. Требования к качественному шифру
Шифр – совокупность обратимых преобразований множества открытых данных на множество зашифрованных данных, заданных алгоритмом криптографического преобразования.
Все современные шифры базируются на принципе Кирхгофа, согласно которому секретность шифра обеспечивается секретностью ключа, а не секретностью алгоритма шифрования. (Делать секретным алгоритм нерационально, а возможности противника лучше переоценить).
Анализируя надежность систем, мы предполагаем, что противник имеет всю информацию о применяемом алгоритме шифрования, ему неизвестен только реально использованный ключ.
Шифрование – понижение ясности сообщения, уменьшение избыточности.
Требования (необходимые условия стойкости криптосистемы, проверяемые статистическими методами):
Соблюдение правила Кирхгофа (надежность любого шифра определяется только секретностью ключа).
Отсутствие статистической зависимости между входной и выходной последовательностями.
Выходная последовательность по своим статистическим свойствам должна быть похожа на случайную.
При неизменной входной информационной последовательности любое изменение ключа должно приводить к существенному непредсказуемому изменению выходной последовательности.
При неизменном ключе любое изменение входной последовательности должно приводить к существенному непредсказуемому изменению выходной последовательности (должно измениться до 50% битов).
Не должно быть зависимостей между ключами, последовательно используемыми в процессе шифрования.
Качественный шифр нельзя раскрыть способом более эффективным, чем полный перебор по всему ключевому пространству.
6. Требования к качественному ГПСЧ
Эффективность стохастических методов ОБИ определяется в первую очередь качеством используемых ГПСП. Качественный ГПСП, ориентированный на использование в задачах защиты информации, должен удовлетворять следующим требованиям:
Непредсказуемость (по сути, криптографическая стойкость).
Хорошие статистические свойства, ПСП по своим статистическим свойствам не должна отличаться от истинно случайной последовательности.
Большой период формулируемой последовательности, учитывая, что при преобразовании больших массивов данных каждому элементу входной последовательности необходимо ставить в соответствие свой элемент ПСП.
Эффективная программная и аппаратная реализация.
При использовании непредсказуемого генератора ПСП три следующие задачи для противника или аналитика, не знающих ключевой информации, вычислительно неразрешимы:
Определение предыдущего (i-1) – го элемента уi-1 последовательности на основе известного фрагмента последовательности yi yi+1 ......yi+b-1 конечной длины b (непредсказуемость влево).
Определение последующего (i+b) – го элемента уi+b последовательности на основе известного фрагмента последовательности yi yi+1 ......yi+b-1 конечной длины b (непредсказуемость вправо).
Определение ключевой информации по известному фрагменту последовательности конечной длины.
Непредсказуемый влево ГПСП является криптостойким.
В рамках другого подхода к построению качественного ГПСП предлагается свести задачу построения криптографически сильного ГПСП к задаче построения статистически безопасного генератора:
Ни один статистический тест не обнаруживает в ПСП каких-либо закономерностей, иными словами, не отличает эту последовательность от истинно случайной.
Нелинейное преобразование Fk, зависящее от секретной информации (ключа К), используемое для построения генератора, обладает свойством «размножения» искажений – все выходные вектора Е’ возможны и равновероятны независимо от исходного вектора Е.
При инициализации случайными значениями генератор порождает статистически независимые ПСП.
7. Модель криптосистемы с секретным ключом.
E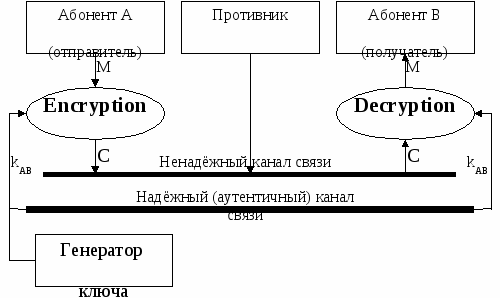 – процесс зашифрования
D – процесс расшифрования.
М– исходный текст.
C – зашифрованный текст.
В информационных отношениях принимают участие три действующих лица: отправитель А, получатель В, противник W. Современные одноключевые криптосистемы предполагают использование взаимно-обратных преобразований E (encryption), D (decryption) блоков данных фиксированной длины.
Для задания блочной криптосистемы необходимо определить:
Числовые параметры криптоалгоритма – разрядность n шифруемых блоков данных, объем ключевой информации, размер раундового ключа, число раундов шифрования.
Раундовую функцию F шифрования.
Алгоритм получения раундовых ключей из исходного ключа kab.
Задача абонента А заключается в том, чтобы передать получателю конфиденциальное сообщение М, состоящее из t блоков длины n.
Задача абонента В заключается в том, чтобы получив переданное сообщение С, понять его содержание.
Для того, чтобы получатель мог прочитать посланное сообщение, отправитель преобразует открытый текст М с помощью функции зашифрования Е и секретного ключа (известного только А и В) kab в шифротекст С: С = ЕАВ(М), который поступает в канал связи.
Получатель восстанавливает исходный текст с помощью функции расшифрования D и того же секретного ключа kab.: М = DАВ(С).
Для реализации такого информационного обмена должен существовать надежный канал, по которому происходит предварительный обмен секретными ключами, а у одного из его законных участников должен быть генератор, формирующий качественные ключи, обеспечивающие гарантированную стойкость системы.
|
|
|
Скачать 2.35 Mb.