Срс. СРС русс. 1. Задумано двузначное число. Найти вероятность того, что задуманным числом окажется а случайно названное

• Название: 1. Задумано двузначное число. Найти вероятность того, что задуманным числом окажется а случайно названное
• Дата: 21.10.2022
• Размер: 2.7 Mb.
• Имя файла: СРС русс.docx
• Тип: Документы; #746178

СРС 1

1. Задумано двузначное число. Найти вероятность того, что не менее 3-х ламп из 5 останутся исправными">Найти вероятность

того, что задуманным числом окажется: а) случайно названное

двузначное число; б) случайно названное двузначное

число, цифры которого различны.

5. Брошены две игральные кости. Найти вероятности

следующих событий: а) сумма выпавших очков равна семи;

б) сумма выпавших очков равна восьми, а разность —

четырем; в) сумма выпавших очков равна восьми, если

известно, что их разность равна четырем; г) сумма выпавших

очков равна пяти, а произведение — четырем.

6. Куб, все грани которого окрашены, распилен на

тысячу кубиков одинакового размера, которые затем тщательно

перемешаны. Найти вероятность того, что наудачу

извлеченный кубик имеет окрашенных граней: а) одну;

б) две; в) три.

7. Монета брошена два раза. Найти вероятность того,

что хотя бы один раз появится «герб».

8. В коробке шесть одинаковых, занумерованных кубиков.

Наудачу по одному извлекают все кубики. Найти

вероятность того, что номера извлеченных кубиков появятся

в возрастающем порядке.

9. Найти вероятность того, что при бросании трех

игральных костей шестерка выпадет на одной (безраз-

лично какой) кости, если на гранях двух других костей

выпадут числа очков, не совпадающие между собой (и неравные шести)

14. В ящике 100 деталей, из них 10 бракованных. Наудачу

извлечены четыре детали. Найти вероятность того,

что среди извлеченных деталей: а) нет бракованных; б)

нет годных.

15. Устройство состоит из пяти элементов, из которых

два изношены. При включении устройства включаются

случайным образом два элемента. Найти вероятность того,

что включенными окажутся неизношенные элементы.

16. Набирая номер телефона, абонент забыл последние

три цифры и, помня лишь, что эти цифры различны,

набрал их наудачу. Найти вероятность того, что набраны

нужные цифры.
СРС 2

36. На отрезке О А длины L числовой оси Ох наудачу

поставлены две точки В{х) и С (у). Найти вероятность

того, что длина отрезка ВС меньше расстояния от точки О

до ближайшей к ней точке. Предполагается, что вероятность

попадания точки на отрезок пропорциональна

длине отрезка и не зависит от его расположения на числовой оси.

37. На отрезке О А длины L числовой оси Ох наудачу

поставлены две точки: В(х) и С (у), причем у 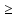х. Найти

вероятность того, что длина отрезка ВС окажется меньше,

чем L/2. Предполагается, что вероятность попадания

точки на отрезок пропорциональна длине отрезка и не

зависит от его расположения на числовой оси.

38. На отрезке О А длины L числовой оси Ох наудачу

поставлены две точки: В{х) и С {у). Найти вероятность

того, что длина отрезка ВС окажется меньше, чем L/2.

Предполагается, что вероятность попадания точки на

отрезок пропорциональна длине отрезка и не зависит от

его расположения на числовой оси.

42. Задача о встрече. Два студента условились встретиться

в определенном месте между 12 и 13 часами дня.

Пришедший первым ждет второго в течение 1/4 часа,

после чего уходит. Найти вероятность того, что встреча

состоится, если каждый студент наудачу выбирает момент

своего прихода (в промежутке от 12 до 13 часов).

43*. Найти вероятность того, что из трех наудачу

взятых отрезков длиной не более L можно построить

треугольник. Предполагается, что вероятность попадания

точки в пространственную фигуру пропорциональна

объему фигуры и не зависит от ее расположения.

Указание. Ввести в рассмотрение пространственную систему

координат.

44. Наудачу взяты два положительных числа х и у,

каждое из которых не превышает двух. Найти вероятность

того, что произведение ху будет не больше единицы,

а частное у/х не больше двух.

45. Наудачу взяты два положительных числа х и j,

каждое из которых не превышает единицы. Найти вероятность

того, что сумма х + у не превышает единицы,

а произведение ху не меньше 0,09

СРС 3

87. Вероятность хотя бы одного попадания в цель

при четырех выстрелах равна 0,9984. Найти вероятность

попадания в цель при одном выстреле.

88. Многократно измеряют некоторую физическую

величину. Вероятность того, что при считывании показаний

прибора допущена ошибка, равна р. Найти наименьшее

число измерений, которое необходимо произвести,

чтобы с вероятностью Р > а можно было ожидать, что

хотя бы один результат измерений окажется неверным.

92. В пирамиде пять винтовок, три из которых снабжены

оптическим прицелом. Вероятность того, что стрелок

поразит мишень при выстреле из винтовки с оптическим

прицелом, равна 0,95; для винтовки без оптического

прицела эта вероятность равна 0,7. Найти вероятность

того, что мишень будет поражена, если стрелок произведет

один выстрел из наудачу взятой винтовки.

93. В ящике содержится 12 деталей, изготовленных

на заводе № 1, 20 деталей—на заводе № 2 и 18 деталей—

на заводе № 3. Вероятность того, что деталь, изготовленная

на заводе № 1, отличного качества, равна 0,9;

для деталей, изготовленных на заводах № 2 и № 3, эти

вероятности соответственно равны 0,6 и 0,9. Найти

вероятность того, что извлеченная наудачу деталь окажется

отличного качества.

94. В первой урне содержится 10 шаров, из них 8

белых; во второй урне 20 шаров, из них 4 белых. Из

каждой урны наудачу извлекли по одному шару, а затем

из этих двух шаров наудачу взят один шар. Найти

вероятность того, что взят белый шар.

95. В каждой из трех урн содержится 6 черных и 4

белых шара. Из первой урны наудачу извлечен один

шар и переложен во вторую урну, после чего из второй

урны наудачу извлечен один шар и переложен

в третью урну. Найти вероятность того, что шар, наудачу

извлеченный из третьей урны, окажется белым,

9в. Вероятности того, что во время работы цифровой

электронной машины произойдет сбой в арифметическом

устройстве, в оперативной памяти, в остальных устройствах,

относятся как 3:2:5. Вероятности обнаружения

сбоя в арифметическом устройстве, в o оперативной памяти

и в остальных устройствах соответственно равны 0,8; 0,9;

0,9. Найти вероятность того, что возникший в машине

сбой будет обнаружен.

СРС4

98. В пирамиде 10 винтовок, из которых 4 снабжены

оптическим прицелом. Вероятность того, что стрелок

поразит мишень при выстреле из винтовки с оптическим

прицелом, равна 0,95; для винтовки без оптического

прицела эта вероятность равна 0,8. Стрелок поразил

мишень из наудачу взятой винтовки. Что вероятнее:

стрелок стрелял из винтовки с оптическим прицелом

или без него?

99. Число грузовых автомашин, проезжающих по

шоссе, на котором стоит бензоколонка, относится к числу

легковых машин, проезжающих по тому же шоссе как

3:2. Вероятность того, что будет заправляться грузовая

машина, равна 0,1; для легковой машины эта вероятность

равна 0,2. К бензоколонке подъехала для заправки

машина. Найти вероятность того, что это грузовая машина.

100. Две перфораторщицы набили на разных перфораторах

по одинаковому комплекту перфокарт. Вероятность

того, что первая перфораторщица допустит ошибку, равна

0,05; для второй перфораторщицы эта вероятность

равна 0,1. При сверке перфокарт была обнаружена

ошибка. Найти вероятность того, что ошиблась первая

перфораторш^ица. (Предполагается, что оба перфоратора

были исправны.)

101. В специализированную больницу поступают

в среднем 50% больных с заболеванием /С, 30%—с заболеванием

L, 20%—с заболеванием М. Вероятность

полного излечения болезни К равна 0,7; для болезней L

и М эти вероятности соответственно равны 0,8 и 0,9.

Больной, поступивший в больницу, был выписан здоровым.

Найти вероятность того, что этот больной страдал

заболеванием К.

102. Изделие проверяется на стандартность одним из

двух товароведов. Вероятность того, что изделие попадет

к первому товароведу, равна 0,55, а ко второму—0,45.

Вероятность того, что стандартное изделие будет признано

стандартным, первым товароведом, равна 0,9, а вторым —

0,98. Стандартное изделие при проверке было признано

стандартным. Найти вероятность того, что это изделие

проверил второй товаровед.

104. Событие А может появиться при условии появления

одного из несовместных событий (гипотез) В₁,В₂,. . . , В

образующих полную группу событий. После появления

события А были переоценены вероятности гипотез,

т. е. были найдены условные вероятности этих гипотез,

причем оказалось, что P_A(B₁) = 0,6 и P_A(B2) = 0,3. Чему

равна условная вероятность P_A(B₃) гипотезы В₃?

СРС 5

126. Вероятность появления события в каждом из 2100

независимых испытаний равна 0,7. Найти вероятность

того, что событие появится: а) не менее 1470 и не более

1500 раз; б) не менее 1470 раз; в) не более 1469 раз.

127. Вероятность появления события в каждом из 21

независимых испытаний равна 0,7. Найти вероятность

того, что событие появится в большинстве испытаний.

129. Вероятность появления события в каждом из

независимых испытаний равна 0,8. Сколько нужно произвести

испытаний, чтобы с вероятностью 0,9 можно было

ожидать, что событие появится не менее 75 раз?
СРС 6

137. Вероятность появления события в каждом из независимых

испытаний равна 0,2. Найти наименьшее число

испытаний п, при котором с вероятностью 0,99 можно

ожидать, что относительная частота появлений события

отклонится от его вероятности по абсолютной величине

не более чем на 0,04.

138. В урне содержатся белые и черные шары в отношении

4:1. После извлечения шара регистрируется его

цвет и шар возвращается в урну. Чему равно наименьшее

число извлечений п, при котором с вероятностью 0,95

можно ожидать, что абсолютная величина отклонения

относительной частоты появления белого шара от его

вероятности будет не более чем 0,01?

139. Вероятность появления события в каждом из 400

независимых испытаний равна 0,8. Найти такое положительное

число 8, чтобы с вероятностью 0,99 абсолютная

величина отклонения относительной частоты появления

события от его вероятности 0,8 не превысила е.

158. Прибор состоит из пяти независимо работающих

элементов. Вероятность отказа элемента в момент включения

прибора равна 0,2. Найти: а) наивероятнейшее

число отказавших элементов; б) вероятность наивероят-

нейшего числа отказавших элементов; в) вероятность отказа

прибора, если для этого достаточно, чтобы отказали

хотя бы четыре элемента.
СРС 7
167. В партии 10% нестандартных деталей. Наудачу

отобраны четыре детали. Написать биномиальный закон

распределения дискретной случайной величины X—числа

нестандартных деталей среди четырех отобранных и построить

многоугольник полученного распределения.

168. Написать биномиальный закон распределения

дискретной случайной величины X—числа появлений

«герба» при двух бросаниях монеты.

169. Две игральные кости одновременно бросают два

раза. Написать биномиальный закон распределения дискретной

случайной величины X—числа выпадений четного

числа очков на двух игральных костях.

180. Магазин получил 1000 бутылок минеральной

воды. Вероятность. того, что при перевозке бутылка окажется

разбитой, равна 0,003. Найти вероятности того,

что магазин получит разбитых бутылок: а) ровно две;

б) менее двух; в) более двух; г) хотя бы одну.

СРС 8



200. Отдел технического контроля проверяет изделия

на стандартность. Вероятность того, что изделие стандартно,

равна 0,9. В каждой партии содержится пять

изделий. Найти математическое ожидание дискретной

случайной величины X — числа партий, в каждой из

которых окажется ровно четыре стандартных изделия,—

если проверке подлежит 50 партий


СРС 9


242. В осветительную сеть параллельно включено 20

ламп. Вероятность того, что за время Т лампа будет

включена, равна 0,8. Пользуясь неравенством Чебышева,

оценить вероятность того, что абсолютная величина разности

между числом включенных ламп и средним числом

(математическим ожиданием) включенных ламп за время Т

окажется: а) меньше трех; б) не меньше трех.

243. Вероятность появления события А в каждом

испытании равна 1/2. Используя неравенство Чебышева,

оценить вероятность того, что число X появлений события

А заключено в пределах от 40 до 60, если будет

произведено 100 независимых испытаний.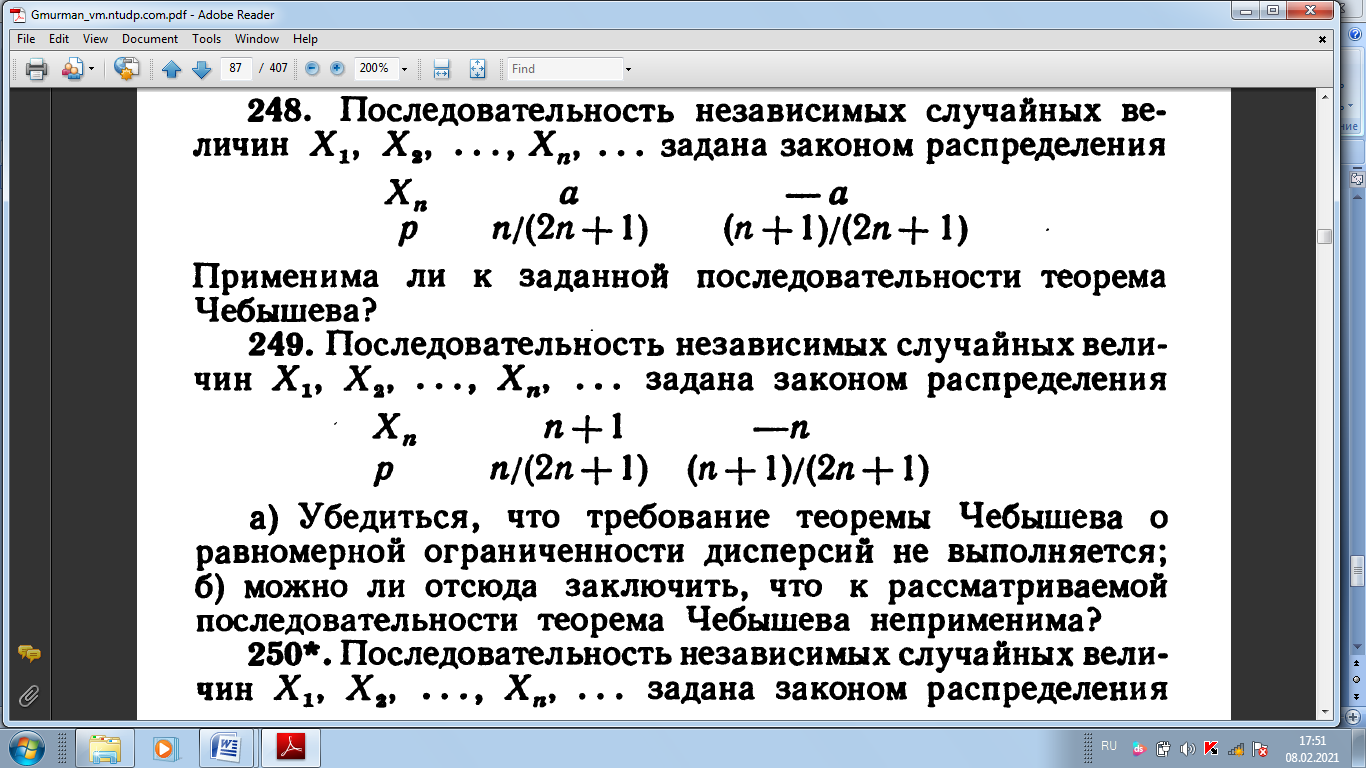


СРС 10



СРС 11

456. По выборке объема л = 51 найдена смещенная

оценка DB = 5 генеральной дисперсии. Найти несмещенную

оценку дисперсии генеральной совокупности

458. В итоге четырех измерений некоторой физической

величины одним прибором (без систематических ошибок)

получены следующие результаты: 8; 9; 11; 12. Найти:

а) выборочную среднюю результатов измерений; б) выборочную

и исправленную дисперсии ошибок прибора.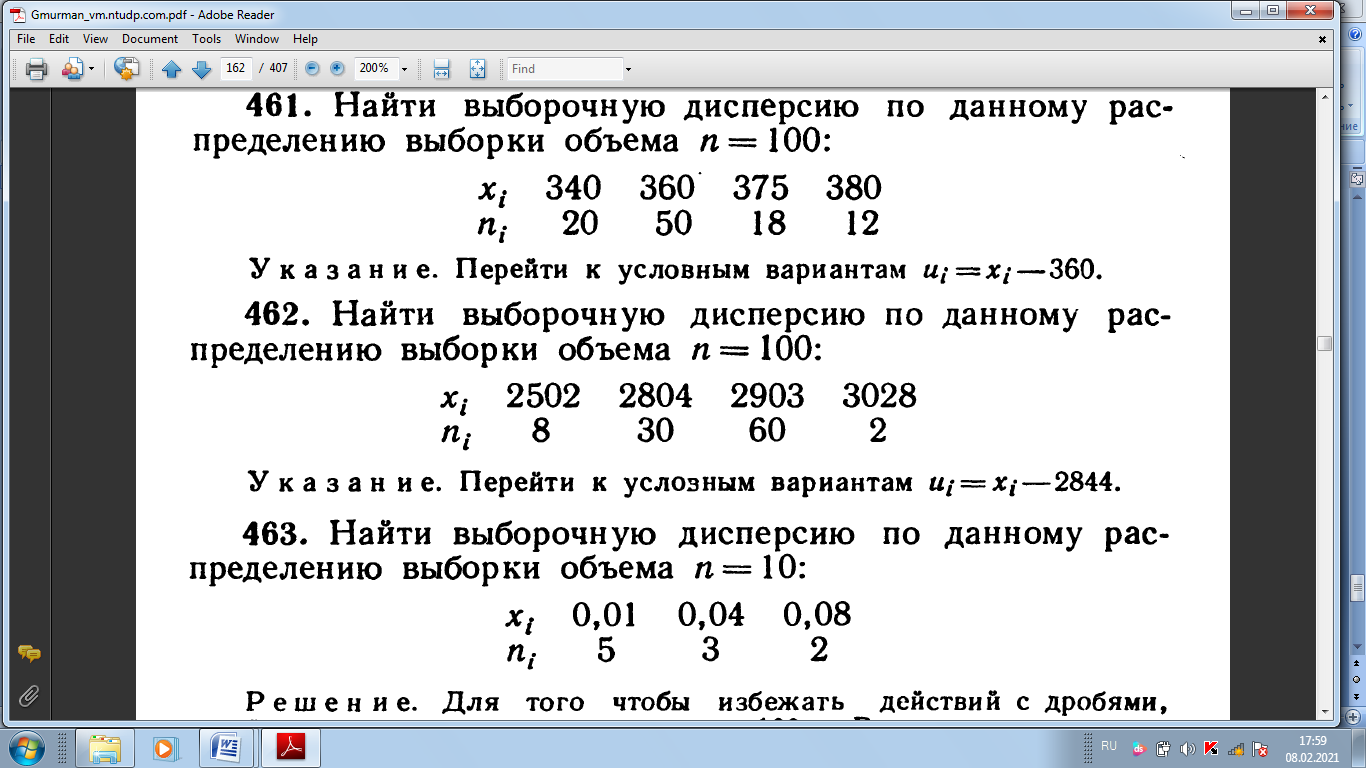



СРС 12, 13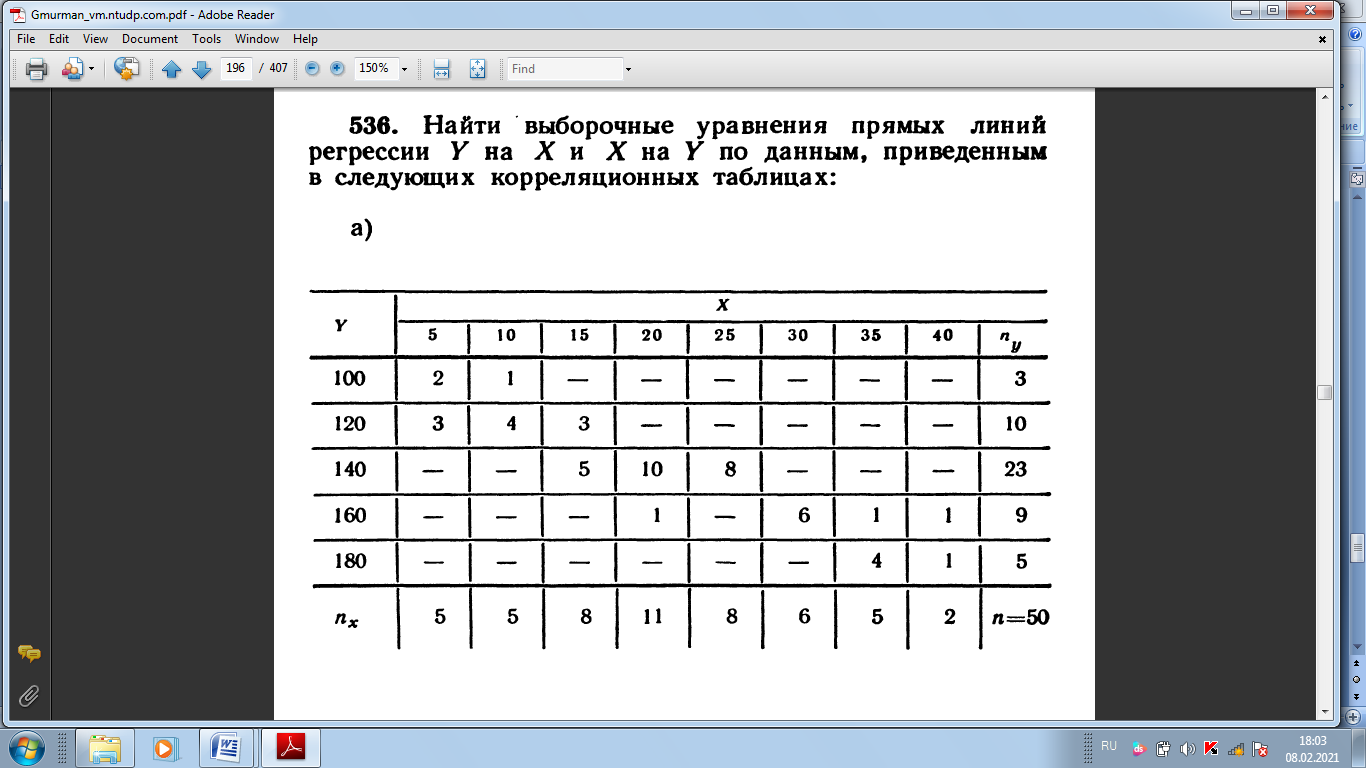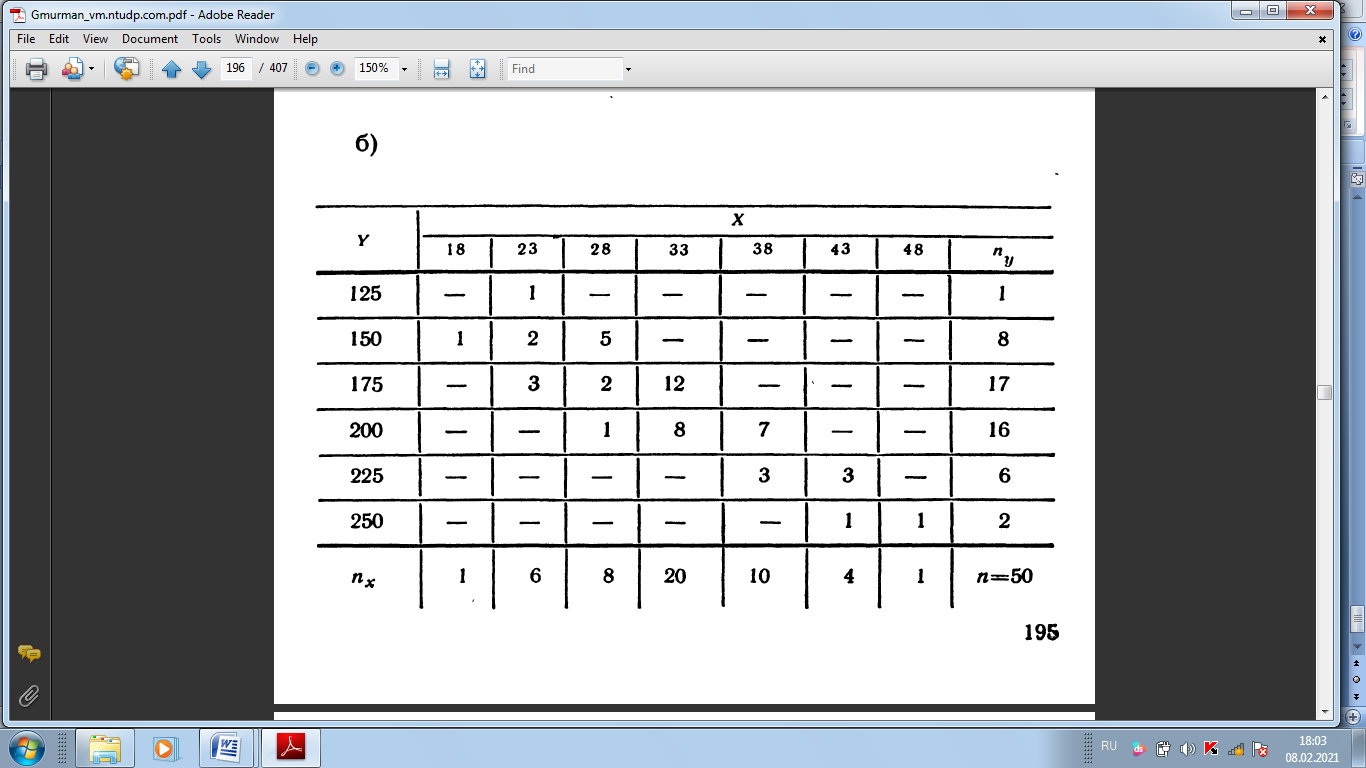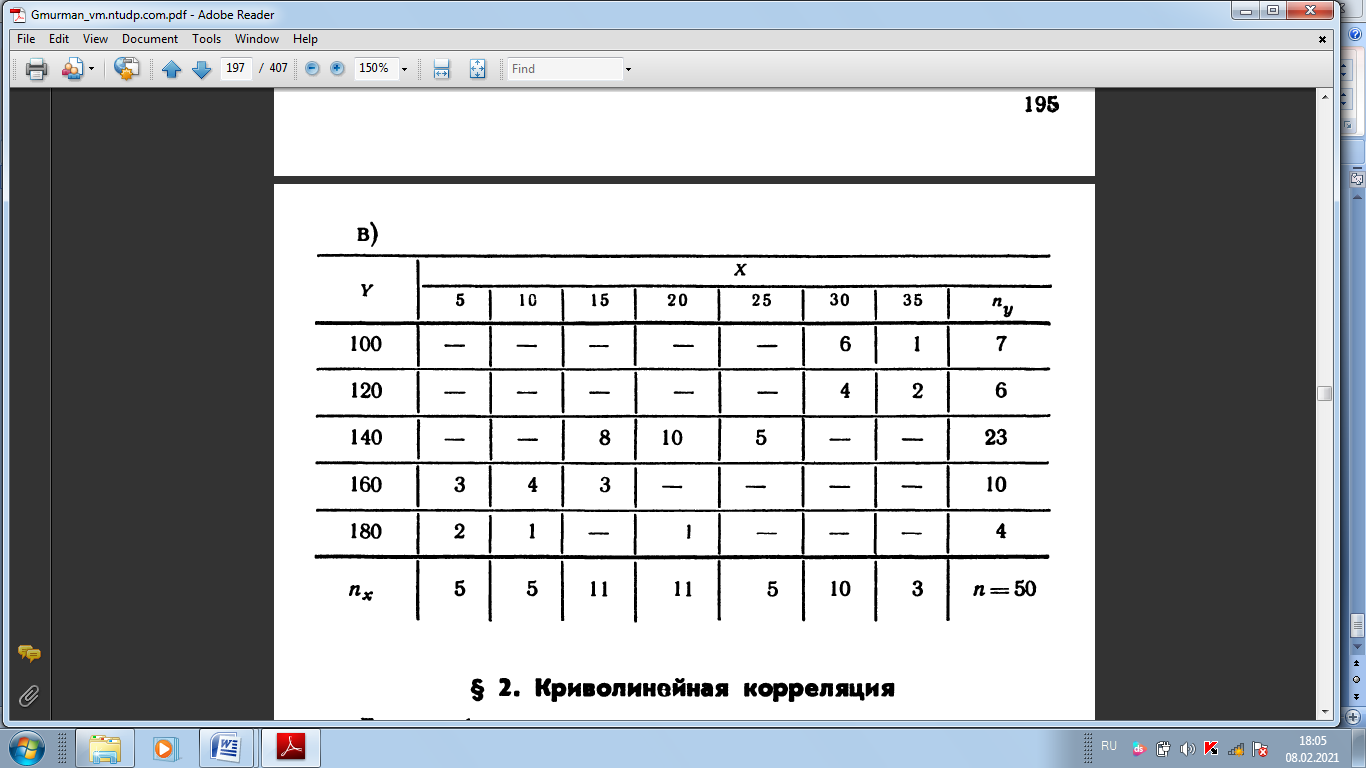






СРС 14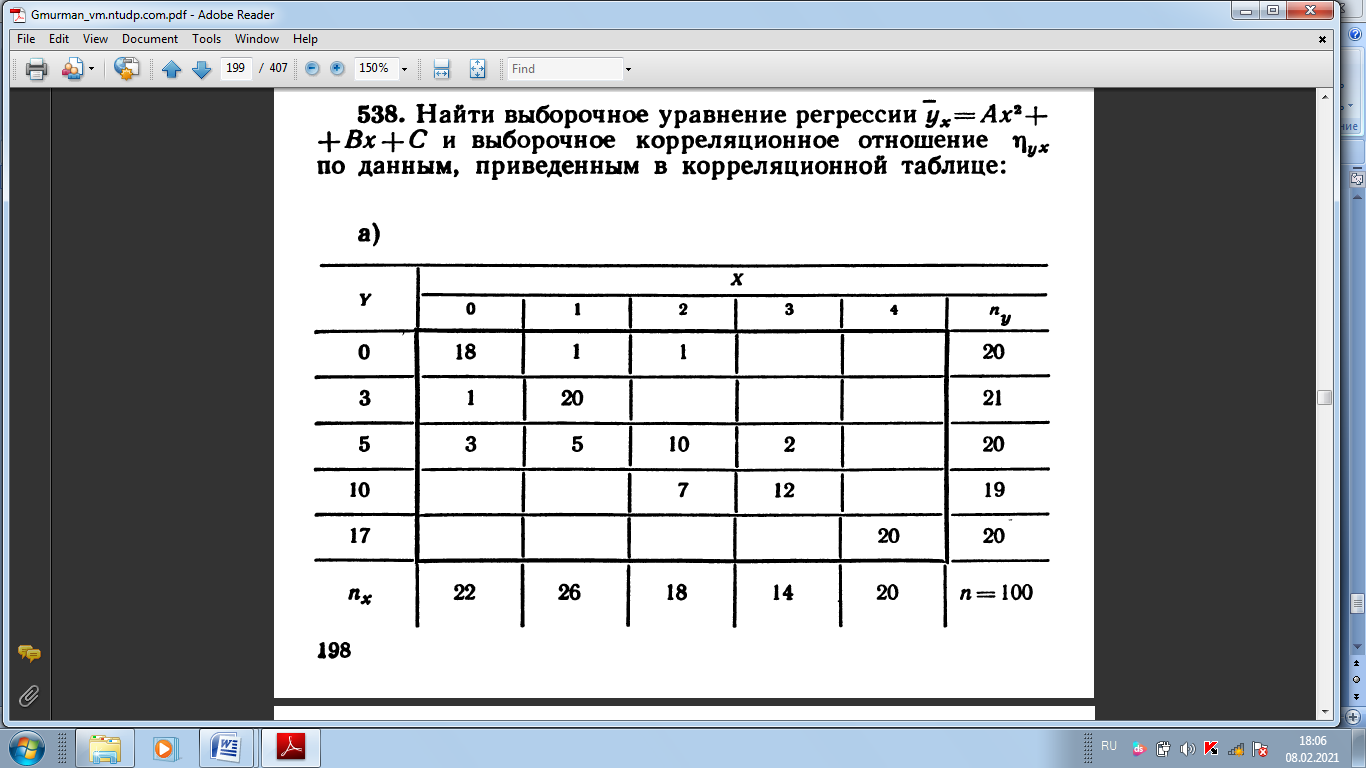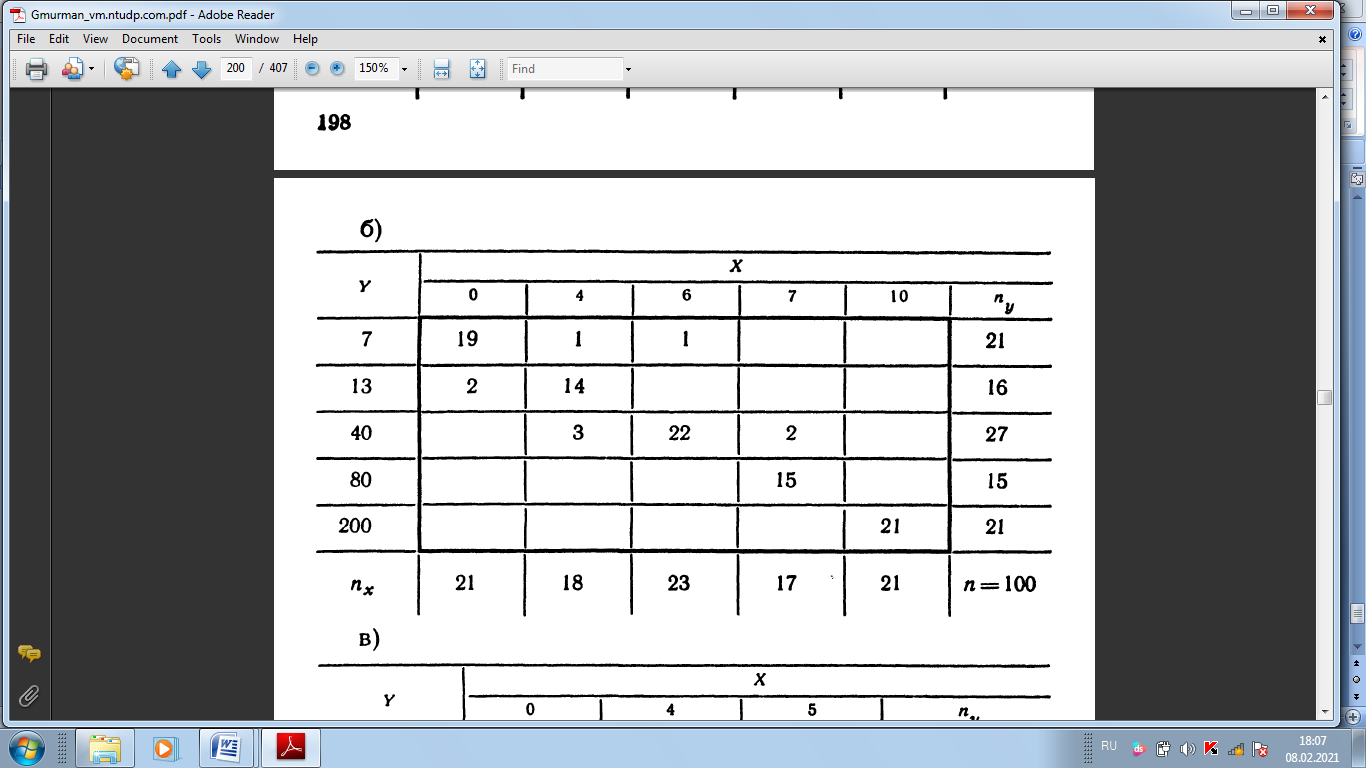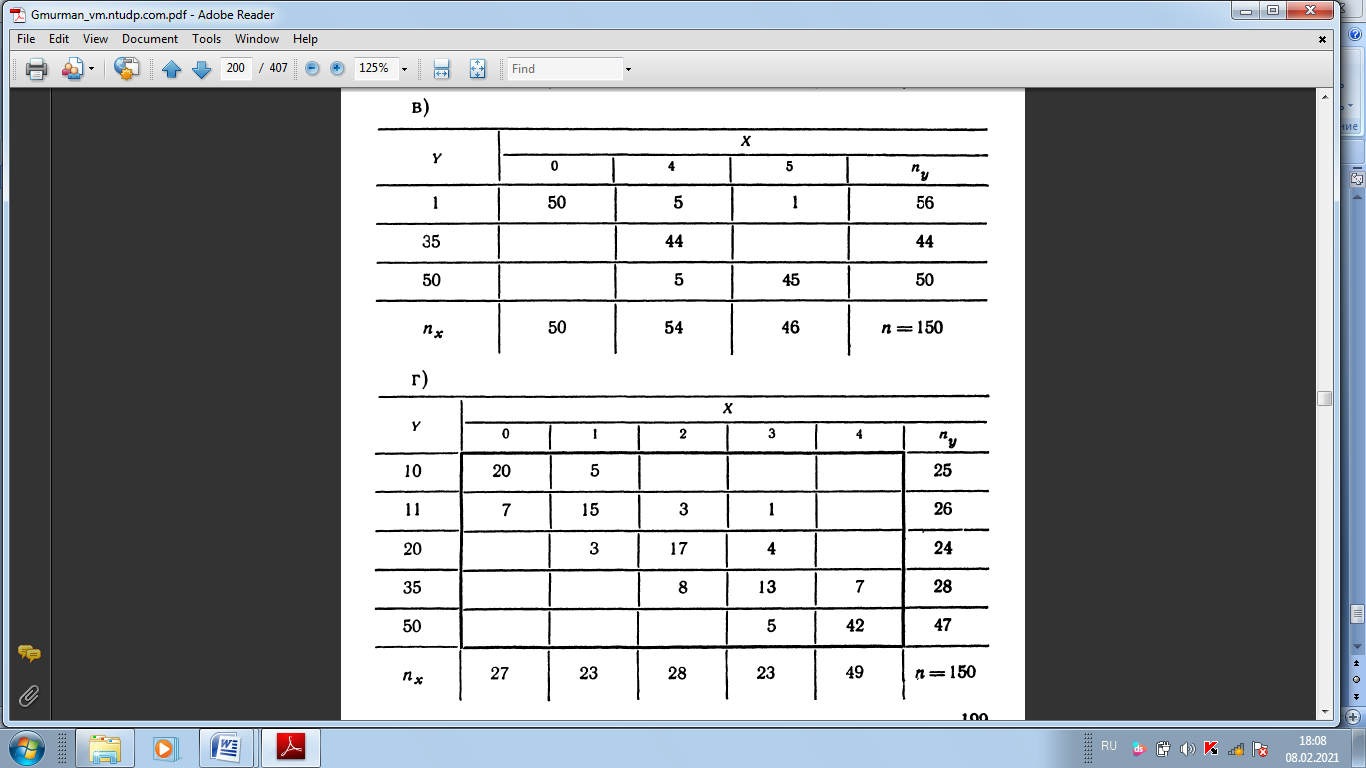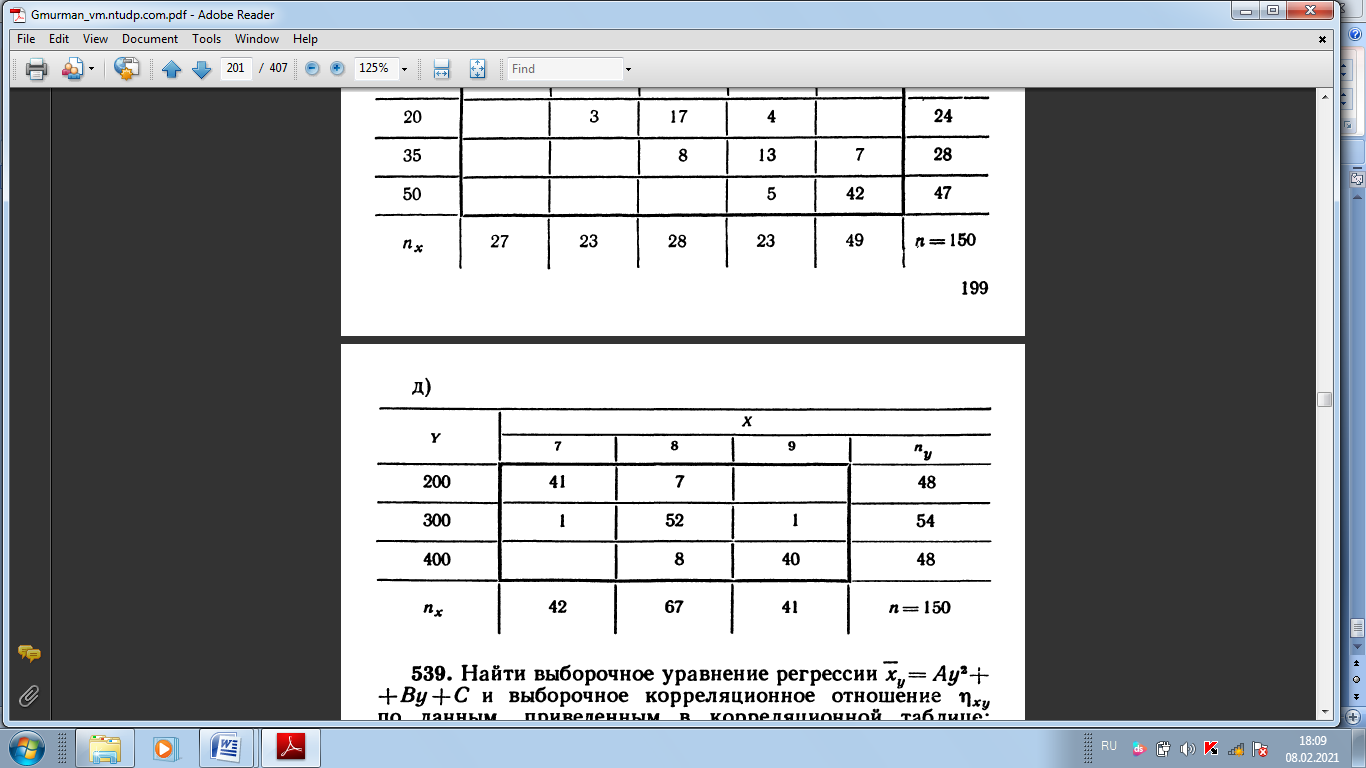






СРС 15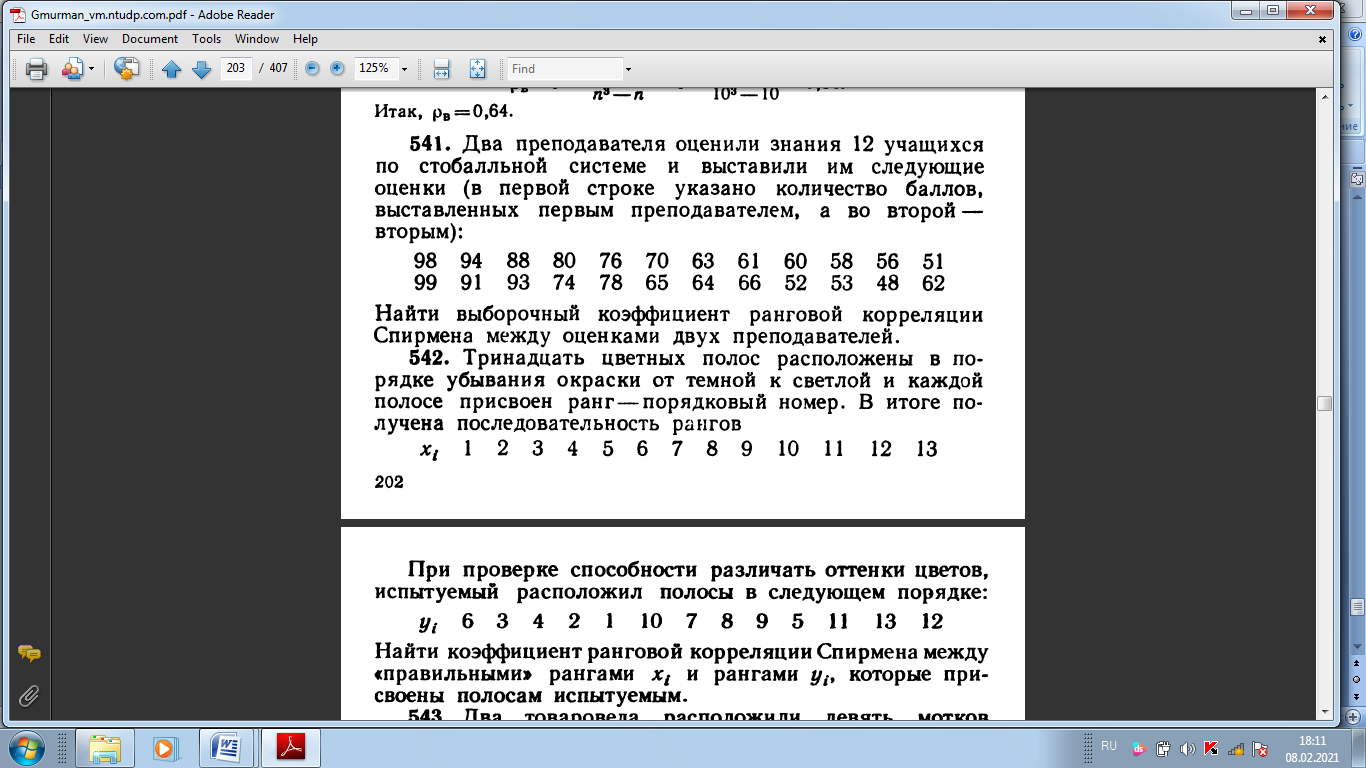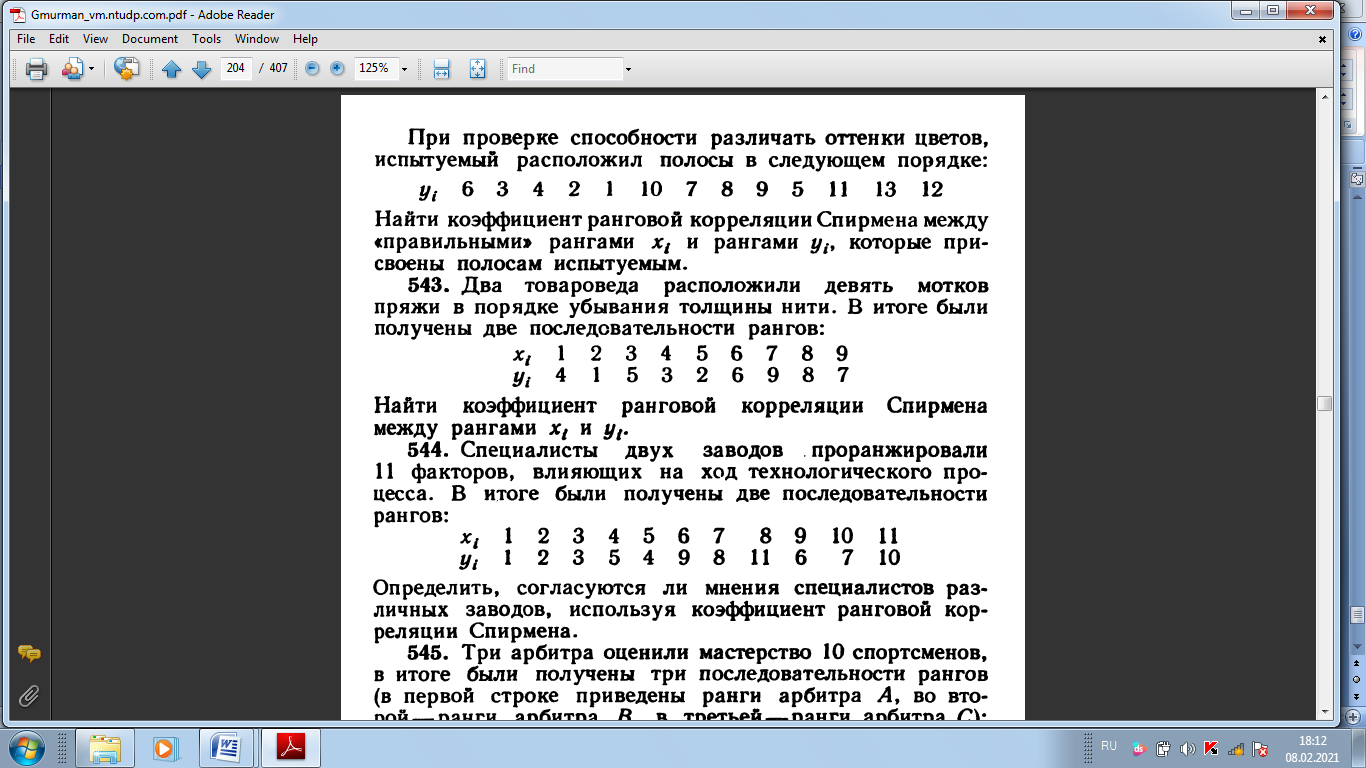