24.Влияние формы и площади загружения на развитие напряжений в грунте.
Построены эпюры нормальных напряжений по вертикальной оси, проходящей через центр квадратного фундамента при (кривая 1), ленточного фундамента (кривая 2), и тоже, шириной (кривая 3).
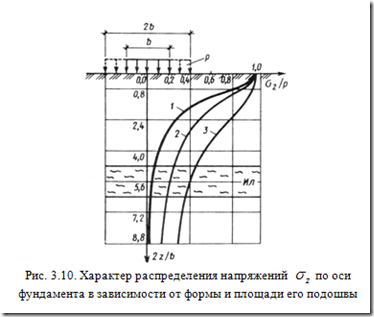
В случае пространственной задачи (кривая 1) напряжения с глубиной затухают значительно быстрее, чем для плоской задачи (кривая 2). Увеличение ширины, а, следовательно, и площади фундамента (кривая 3) приводит к ещё более медленному затуханию напряжений с глубиной.
25.Распределение напряжений при треугольной нагрузке.
Эпюры нормальных напряжений в грунте при действии треугольной нагрузки
Максимальные напряжения возникают в сечении, близком к центру тяжести эпюры интенсивности распределенной нагрузки.
30) создает распределенную нагрузку, изменяющуюся по закону равнобедренного треугольника с максимальной интенсивностью q (см.
Эпюры нормальных напряжений в грунте при действии нагрузки, распределенной по форме равнобедренного треугольника
Максимальная интенсивность распределенной нагрузки q (табл.
Эпюры нормальных напряжений в грунте при действии распределенной трапецеидальной нагрузки
Расчетная схема к определению напряжений в грунте при действии комбинированной полосовой нагрузки
Максимальная интенсивность распределенной нагрузки 2?
Данную эпюру распределенной нагрузки удобно представить в виде двух равнобедренных треугольников BCD и DEF и равнобедренной трапеции ABFG с максимальной интенсивностью q.
Соответственно искомое напряжение в точке М будет складываться из напряжений от выделенных фрагментов эпюры распределенной нагрузки.
Вычисляем относительные координаты и напряжение в точке М от треугольника нагрузки BCD по формуле (45) : х^ = \а + х\ = = |6 - 3| = 3 м; а - ]*,|/я = 3/6= 0,5; /3„ , = z,/a = 12/6 = 2.
Вычисляем относительные координа'ты и напряжение в точке М от треугольника нагрузки DEF: х2 = \а - х\ = |6 + 3| =9 м; а4 = = *2 \а = 9/6 = 1,5; (34 2 = z2/3 = 12/6 = 2.
Условие перехода грунта в предельное напряженное состояние при действии внешней нагрузки имеет вид
Главные напряжения а^ и а2 при действии равномерно распределенной нагрузки <7*вычисляют соответственно по формулам: где q* = q
7.
Схемы к определению главных грунте от угла отклонения в и ориен- напряжений при действии полосовой тации площадки нагрузки
При действии нагрузки, распределенной по закону равнобедренного треугольника и приложенной к поверхности земли, главные напряжения а{ и о2 соответственно определяют по формулам где АЬ и В 6 — коэффициенты, принимаемые по табл.
Соответственно для треугольной нагрузки sin -*б> q(A6 + В6) + 2 + 2 с ctg
Внешнюю равномерно распределенную нагрузку, при которой область предельно напряженного состояния грунта в основании сооружения распространяется на глубину до z.
, называют критической нагрузкой:
Аналогично, внешнюю нагрузку, при действии которой в основании сооружения не возникают области пластической деформации грунта,
1 0,06 0,05 0,048 0,047 0,045 0,006 за исключением краевых точек основания, называют критической краевой нагрузкой:
Максимальная глубина распространения области предельно напряженного состояния грунта при заданной внешней нагрузке q
Оценка прочности грунта в основании сооружений заключается в сопоставлении заданной нагрузки с критической, определении максимальной глубины распространения области предельного состояния грунта и построении контура этой области.
Определить критические нагрузки в основании заглубленного ленточного фундамента шириной 2а, глубиной заложения /, передающего на грунт равномерно распределенную нагрузку интенсивностью q (рис.
Из сопоставления критических нагрузок с заданной: q > q и q > q следует, что в основании фундамента будут наблюдаться пластические деформации грунта.
Размеры сетки по вертикали следует принимать исходя из zmax-Число узлов сетки по горизонтали (1-18) может быть в каждом слое различным в зависимости от расчетных значений 0тах- Ввиду симметричности нагрузки расчеты достаточно выполнять для одной половины сетки.
Расчетная нагрузка q* = q -rec/ =230,44-22,1 • 1,6= 195,08 кПа.
При соединении полученных в результате интерполяции точек между собой плавной линией получим искомую область основания фундамента, внутри которой грунт будет находиться в предельном состоянии под действием внешней нагрузки.
Вычислим вначале параметры треугольника нагрузки.
Максимальная интенсивность распределенной нагрузки, создаваемой грунтовой насыпью, q = = fh =20,5 • 10 = 205к11а.
При наличии распределенной нагрузки, приложенной к поверхности связного грунта, где 7 - удельный вес грунта; г - расстояние от поверхности грунта до рассматриваемого сечения; q — интенсивность распределенной нагрузки; <0 - угол внутреннего трения грунта; с - сцепление грунта.
При расположении распределенной нагрузки на некотором удалении а от бровки откоса активное давление
При наличии распределенной нагрузки, приложенной к поверхности грунта,?
В связи с тем что грунт однородный несвязный, а внешняя нагрузка отсутствует, для построения линейной эпюры активного и пассивного давлений достаточно определить к\ значения на уровне подошвы подпорной стенки.
|
 Скачать 1.01 Mb.
Скачать 1.01 Mb.