Для моделирования обслуживания клиентов в банке предложена следующая модель:
за 1 минуту в банк входит случайное число клиентов, от 0 до 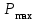 (распределение равномерное); (распределение равномерное);
на обслуживание клиентов требуется от 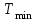 до до 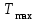 минут; время обслуживания минут; время обслуживания 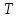 определяется для каждой рабочей минуты случайным образом (распределение равномерное); определяется для каждой рабочей минуты случайным образом (распределение равномерное);
моделирование выполняется для интервала времени 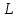 , равного 8-часам (рабочая смена). , равного 8-часам (рабочая смена).
число клиентов, находящихся в помещении банка, вычисляется по формуле
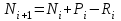
где 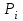 – количество клиентов, вошедших за – количество клиентов, вошедших за 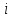 -ую минуту, а -ую минуту, а 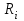 – количество клиентов, обслуженных за это время; – количество клиентов, обслуженных за это время;
если кассир обслуживает клиента за 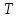 минут, то можно считать, что за 1 минуту он сделает часть работы, равную минут, то можно считать, что за 1 минуту он сделает часть работы, равную 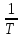 ; если предположить, что скорость работы кассиров одинакова, то ; если предположить, что скорость работы кассиров одинакова, то 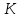 касс за 1 минуту обслужат касс за 1 минуту обслужат 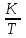 клиентов; клиентов;
если считать, что 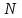 клиентов равномерно распределяются по клиентов равномерно распределяются по 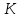 кассам, так что средняя длина очереди равна кассам, так что средняя длина очереди равна 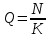 , а среднее время ожидания в течение этой минуты равно , а среднее время ожидания в течение этой минуты равно
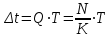
достаточным считается число касс, при которых среднее время ожидания 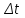 превышает установленный предел превышает установленный предел 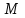 не более, чем 5% рабочего времени в течение дня. не более, чем 5% рабочего времени в течение дня.
Используя эту вероятностную модель работы банка, напишите программу, с помощью которой определите минимальное необходимое количество касс при следующих исходных данных:
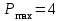 , , 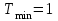 , , 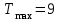 , , 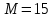 . .
import random
wt = 100 #рабочее время в процентах
K = 0 #количество кассиров
while wt > 0.05:
N = 0 #начальное число посетителей банка
Pmax = 4 #максимальное число входящих за 1 минуту
Tmin = 1 #минимальное время обслуживания
Tmax = 9 #максимальное время обслуживания
M = 15 #допустимое время ожидания
count = 0 #счётчик минут, выше чем 15+0.05%
L = 480 #период моделирования в минутах (рабочая смена 8 часов)
K = K + 1 #количество кассиров
for i in range(L):
P = random.randint(0, Pmax) #случайное количество входящих
T = random.randint(Tmin, Tmax) #случайное время обслуживания
R = K // T #число клиентов, обслуженных за минуту
N += P - R #число клиентов в банке
if N < 0:
N = 0
dT = N * K / T
if dT > M: #время ожидания
count = count + 1
wt = count / L
print(K)
Ответ: 10 |
 Скачать 41.49 Kb.
Скачать 41.49 Kb.