Дз Управаленеие в технических системах. 16-17, Управление в тех. системах. 16. Построение логарифмических частотных характеристик

• Название: 16. Построение логарифмических частотных характеристик
• Анкор: Дз Управаленеие в технических системах
• Дата: 19.04.2021
• Размер: 33.78 Kb.
• Имя файла: 16-17, Управление в тех. системах.docx
• Тип: Документы; #196189

16. Построение логарифмических частотных характеристик.

[Ниже написал всякие свойства и особенности именно ЛАЧХ и ЛФЧХ . На практике же, мы пользуемся тем, что систему можно представить в виде параллельно включенных типовых динамических звеньев, для которых эти графики уже известны]

Логарифмическая амплитудно-частотная характеристика (логарифмическая амплитудная характеристика, ЛАХ) L(w) определяется путем преобразования амплитудно-частотной характеристики (АЧХ) Aw):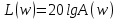



и имеет единицу измерения – децибел (дБ).

При построении рассматриваемых характеристик для горизонтальной оси (оси частот) используется логарифмический масштаб, другими словами, в обычном линейном масштабе по горизонтальной оси откладываются не сами частоты w, а значения lg w. Угловая частота, как и обычно, измеряется в 1/с (рад/с), но в силу применяемого масштаба единицей измерения по оси абсцисс является декада.

Отметим следующие обстоятельства, характерные для используемого логарифмического масштаба: 1. Отрицательные частоты не рассматриваются.

2. Отметка частоты w=0 на оси отсутствует. При 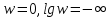, и соответствующие отметки частоты смещаются по горизонтальной оси влево в бесконечность.

3. Вертикальная ось проводится через отметку частоты, соответствующую нижней границе диапазона существенных частот для изображаемых характеристик.

4. Изменению значения частоты в k раз соответствует отрезок оси постоянной длины независимо от его расположения на оси (то есть абсолютных значений частот).

5. Отрезок горизонтальной оси, соответствующий десятикратному изменению частоты, называется декадой. Длина декады, очевидно, постоянна независимо от ее расположения на оси.

Логарифмическая фазо-частотная характеристика строится совместно с ЛАХ, причем горизонтальная ось у обеих характеристик полностью совпадает, а вертикальная ось для ЛФЧХ совмещается с вертикальной осью ЛАХ следующим образом:

1.Направление положительного отсчета значений ЛФЧХ – вниз.

2. С отметкой 0 дБ для ЛАХ (пересечение с горизонтальной осью) совмещается отметка -180° для ЛФЧХ (рис.1).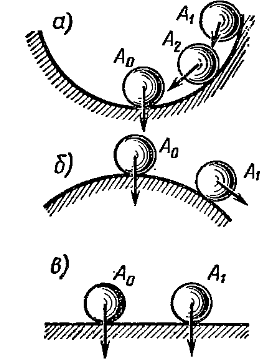

17. Устойчивость линейных систем. Понятие устойчивости.

• 
  Устойчивая система – это динамическая система, обладающая ограниченной реакцией на ограниченный входной сигнал.
  

На картинке a) устойчивое равновесие б) неустойчивое в) безразличное.

• 
  Определяется так:
  

у₁^*(t), y₂^*(t), …, y_n^*(t) - невозмущенное движение, у₁(t), y₂(t), …, y_n(t) - возмущенное движение, при этом:

у₁(t)y₁^*(t), у₂(t)y₂^*(t), … , у_n(t)y_n^*(t).

Заданное невозмущенное движение будет устойчивым, если после приложения внешних сил (возмущений), которые затем снимают, возмущенное движение по истечении некоторого времени войдет в заданную область y_i(t) – y_i^*(t)_i, где _i = const – заданные величины, i = 1, 2, …, n.

• 
  Невозмущенное движение называют устойчивым по отношению к переменным x_i, если при всяком произвольно заданном положительном числе , как бы мало оно ни было, можно выбрать другое такое положительное число (), что при всяких возмущениях x_i0, удовлетворяющих условию: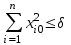
  

и при любом t  t₀ будет выполняться неравенство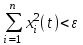



в противном случае движение неустойчиво.