|
|
18. Метод математической индукции
22. Числовые характеристики графа: цикломатическое число, хроматическое число. Раскраска графов.
Цикломатическим числом ν(G) графа G наз. наименьшее число ребер, удаление которых приводит к графу без циклов; ν(G) =m-n+k. где т - число ребер, n - число вершин, k - число компонент связности графа G.
Хроматическим числом χ(G) наз. наименьшее количество цветов, которыми можно раскрасить вершины графа G так, чтобы любые смежные вершины были окрашены разными цветами.
Правила раскраски графов:
Раскрашиваем вершины графа
2 смежные вершины – разного цвета
Экономим краски.
Начинаем раскрашивать с….
10. Упорядоченные мн-ва, определения, примеры.
Два эл-та aM и bM являются сравнимыми в данном порядке TMM, если про них можно сказать, что (a,b)T или (b,a)T, или a=b.
Мн-во М с введенным порядком Т является упорядоченным (линейно упорядоченным), если любые два эл-та этого мн-ва являются сравнимыми.
Про мн-во М, на котором просто введен некоторый порядок Т, т.е. в котором существуют сравнимые эл-ты, говорят, что оно частично упорядоченно.
Св-вом упорядоченности обладает мн-во всех точек на действительной числовой прямой R, т.к. любые два действительных числа можно сравнить между собой.
Для отношения «быть собственным подмн-вом» это св-во не имеет места, т.к. по отношению включения можно сравнить далеко не все подмн-ва. Например, числовой интервал (-2,5) нельзя сравнить с отр-ком [0,7] по отношению включения. Таким образом, это мн-во является частично упорядоченным.
Среди линейно упорядоченных мн-в выделяют вполне упорядоченные мн-ва. Для его определения введем определение усл-вия минимальности.
Говорят, что мн-во М удовлетворяет усл-вию миним-ти для некот отн-ния порядка Т, если в люб его непуст подмн-ве XM существует такой эл-т a, что x xX, имеет место: аТх.
Итак, мн-во назыв вполне упоряд-ым, если оно явл лин упоряд-ым и удовлетворяет усл-вию миним-ти. Например, мн-во натур чисел явл вполне упоряд-ым, а мн-во действит чисел не явл вполне упорядоченным, т.к. для интервалов не сущ-ет минимального эл-та.
Обратим внимание на то, что одно и то же мн-во может быть линейно упорядоченным относительно одного порядка и лишь частично упорядоченным относительно другого. Например, мн-во людей с введенным отн-ем старшинства явл лин упоряд-ным (роль рав-ва играет отн-ние «быть ровесниками»), а это же мн-во с отн-нием «быть предком» не явл лин упоряд-ным, т.к. про любых 2х людей нельзя сказать, что один явл-ся предком другого.
|
34 Операции над бинарными отношениями
Так как отношения на Х задаются подмножествами rНXґY, для них определимы те же операции, что и над множествами:
Объединение r1Иr2: r1Иr2={(х, у)| (х, у)Оr1 или (х, у)Оr2}.
Пересечение r1Зr2: r1Зr2={(х, у)| (х, у)Оr1 и (х, у)Оr2}.
Разность r1\r2: r1\r2={(х, у)| (х, у)Оr1 и (х, у)П r2}.
Дополнение 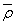 : : 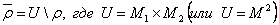 . .
Обратное отношение r -1: х r -1 у тогда и только тогда, когда уrх, r -1={(x, y)| (y, x)Оr}.
Пример 13.
Если r - «быть моложе», то r -1 – «быть старше».
6. Составное отношение (композиция) r1 · r2. Пусть заданы множества М1, М2 и М3 и отношения R1 Н М1 ґ М2 и R2 Н М2 ґ М3. Составное отношение действует из М1 в М2 посредством R1, а затем из М2 в М3 посредством R2, то есть (a, b) О R1·R2, если существует такое с О М2, что (а, с) О R1 и (a, c) О R2.
7. Транзитивное замыкание r°. Транзитивное замыкание состоит из таких и только таких пар элементов а и b из М, то есть (a, b)Оr°, для которых в М существует цепочка из (k+2) элементов М, kі 0, что а, с1, с2, …ck, b, между соседними элементами которой выполняется r. Другими словами а r с1, с1 r с2, …, сk r b.
Пример 14.
Для отношения «быть сыном» транзитивным замыканием является отношение «быть прямым потомком по мужской линии».

|
11. Деревья, лексикографический порядок, определения, примеры.
Имеем некот алфавит. Заметим, что его мощность должна быть не меньше, чем макс число ветвлений в некот вершине дерева. Не ограничивая области, возьмем латин алфавит. Дерево в мате-ке строится сверху вниз. Пусть корень (начальная вершина) дерева назыв a. Тогда в 1ом ярусе самая лев вер-на есть аа, след – ab, затем – ac и т.д., во 2ом ярусе вер-ны, выход из вер-ны aa, имеют названия aaa, aab, aac и т.д., вер-ны, выход из вер-ны ab, имеют названия aba, аbb, аbc и т.д. Таким образом, вер-на, находящаяся в n-м ярусе, имеет названия длины n. Если из вер-ны не выходит ни одной ветви, то она называется концевой.
Пример. В дереве естественным образом устанавливается отн-ние предшествования: одна вер-на предшествует др, если ее имя явл префиксом имени 2ой вер-ны. Так, вершина aa предшествует вер-не aabab. В этом порядке сравнимые вер-ны на 1ой ветви: та, которая находится выше, предшеств той, кот находится ниже. Такой порядок графич иллюстрирует соотн-ние между людьми «быть предком»; вер-ны, располож выше, изображают предка, а вер-ны, располож ниже, - потомков. Если рассматривать дерево на рис как генеал-кое, то аа есть прадед aabab. Разумеется, в этом порядке вер-ны дерева не представляют собой упоряд мн-ва, а лишь частич упоряд мн-во, т.к. вер-ны aaa и ababb не сравнимы.
если имя 1ой является префиксом имени 2ой.
Е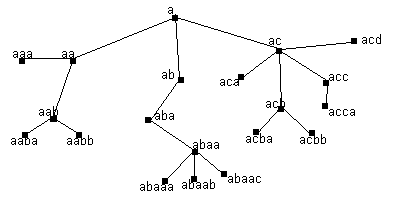 сли все буквы, кроме последней, в них совпадают, а последняя буква в 1ом слове расположена в алфавите раньше, чем последняя буква во 2ом слове. сли все буквы, кроме последней, в них совпадают, а последняя буква в 1ом слове расположена в алфавите раньше, чем последняя буква во 2ом слове.
В дереве на рис вер-на ab предш-ет вер-не ababb, а вер-на ababaa предш-ет вер-не ababab.
В этом порядке число вер-н по-прежнему не явл упоряд-ым мн-вом; к примеру, вер-ны aabb и abab не явл сравнимыми, но теперь можно сравнивать вер-ны, выходящие из одной и той же вер-ны. В отн-ях между людьми это можно интерпретировать как отношение «быть или предком, или старшим братом». Иногда такой порядок называют «деревянным».
Если для некот целей нужно, чтобы все вер-ны дерева были упорядоченными, то порядок можно определить следующим образом. Одна вершина предшествует другой в 2х случаях:
если имя первой явл префиксом имени 2ой
выделяется макс общ префикс 2х имен и далее, если след за макс общ префиксом буква имени 1ой вер-ны расположена раньше, чем такая же буква имени 2ой вершины.
Этот порядок называется лексикографическим, алфавитным или словарным.
|
23. Задачи о кратчайших путях: путь с наим. числом дуг, (путь кратчайшей длины).
Путь наз кратчайшим, если он содержит наименьшее число дуг из всех возможных.
Алгоритм построения наименьшего пути от верш а к верш b.
Присвоить верш а метку 0
Если вершина Х ≠ а и верш Х – смежна с а, то присвоить верш Х метку 1.
Пусть V(m) – мн-во верш, им-х метку m. Тогда V(m+1) – мн-во верш
{x | y, y V(m)} где х и у смежны.
Процесс присвоения прекратить, как только метку получила вершина b.
Рассм послед-ть вершин от верш b {Xi1V(n); Xi2 смежн с Х i1 и Xi2V(n-1);…а=Хim},
{a=Хim, Х(im-1)… Хi1=b} – путь из вершины а в вершину b
|
12. Св-ва отображения, ф-ции графики. Ф-ции как част случай бинар отношений.
Функцией называется функциональное соответствие. Если функция устанавливает соответствие между множествами А и В, то говорят, что функция имеет тип АВ (обозначается АВ). Каждому элементу а из области определения функция ставит в соответствие элемент b из области значений. Это обозначается (а)=b. Элемент а – аргумент функции, элемент b – значение функции на а.
Отображением. А в называется всюду определённая функция. __ АВ.
Отображением А на В называется всюду определённое и при этом сюръективное функциональное соответствие АВ.
Отображением типа АА часто называют преобразованием множества А. Функция типа АА, являющаяся отображением А на А, называется перестановкой на А.
Функции и g равны, если:
Их области определения – одно и то же множество А
Для любого аА (а)=g(а).
Функция типа А1А2…Аn назывется n-местной. В этом случае принято считать, что функция имеет n аргументов: (а1……аn)=b, где а1А1,……..,аnAn, bB.
Если соответствие, обратное к функции АВ, является функциональным, то оно называется функцией, обратной к (обозначается -1). Для функции АВ обратная функция существует тогда и только тогда, когда является взаимно однозначным соответствием между своими областями определения и значений.
Способы задания функции:
Графиком
Таблицей
Формулой, описывающей функцию, как суперпозициюдругих (исходных) функций.
Рекурсивной вычислительной процедурой. Например, функция (х)=1*2*3….*(х – 1)*х=х! Описывается рекурсивной вычислительной процедурой, задаваемой следующими правилами: (0)=1; (х+1)= (х)*(х+1)
Если элемент а принадлежит множеству М, то соответствующий ему элемент d=(a) называется его образом. Каждый элемент а может иметь единственный образ, при этом для b может существовать не один элемент из М, образом котрого он является.
Совокупност всех тех эл-тов а из М, образом которых является данный элемент b из N, называется прообразом или полным прообразом элемента b и обозначается -1(b).
|
24. Теорема об эйлеровом цикле.
Эйлеров цикл – сод-т все ребра графа и ни по одному нельзя пройти 2-ды.
Теоp.Эйлеров цикл в связном графе когда все вершины имеют четную степень.
Док-во. Необход-ть условия очевидна, так как при каждом прохожд цикла через к-либо вершину использ. 2 ребра - по 1 из них маршрут входит в верш, по др вых-т из нее (это относ. и к старт верш - в ней ведь маршрут должен закон-ся). Достаточность.
Пусть G - связн граф, в кот-м > 1 верш и степени всех вершин четны. Значит, степень каждой вершины >= 2, поэтому по теореме (критер прост цикла) в графе G имеется цикл Z1. Если удалить все ребра этого цикла из графа G, то пол-ся граф G1, в кот-м степени вершин также четны. Если в G1 нет ни одного ребра, то Z1- эйлеров цикл. В прот случае, применяя ту же теорему к графу, получ из G1 удалением всех изолир-х верш, заключаем, что в G1 имеется цикл Z2. Удалив из G1 все ребра цикла Z2, получим граф G2. Продолжая действовать т. о., пока не придем к пустому графу, получим в итоге систему циклов Z1….Zk, причем каждое ребро графа в точности одному из них. Покажем теперь, что из этих циклов можно составить один цикл. Действительно, из того, что исходный граф связен, следует, что хотя бы один из циклов Z1…Zk-1 имеет общую вершину с Zk. Допустим, для определенности, что таков цикл Zk-1. Пусть 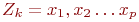 , , 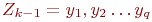 , и Xi =Yj для некоторых i и j. Тогда посл-ть вершин , и Xi =Yj для некоторых i и j. Тогда посл-ть вершин 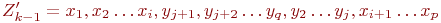 очевидно, является циклом, а множество ребер этого цикла есть объединение множеств ребер циклов Zk-1 и Zk. Таким образом, получаем систему из меньшего числа циклов, по-прежнему обладающую тем свойством, что каждое ребро графа в точности одному из них. Действуя далее таким же образом, в конце концов, получим один цикл, который и будет эйлеровым. очевидно, является циклом, а множество ребер этого цикла есть объединение множеств ребер циклов Zk-1 и Zk. Таким образом, получаем систему из меньшего числа циклов, по-прежнему обладающую тем свойством, что каждое ребро графа в точности одному из них. Действуя далее таким же образом, в конце концов, получим один цикл, который и будет эйлеровым.
|
13. Свойства функций: инъективность, сюрьективность, биективность.
1.Функция f называется инъективной (или, коротко, инъекция), если разным элементам множества X сопоставлены разные элементы множества Y. Более формально, функция f инъективна, если для любых двух элементов X1, X2 X таких, что f(x1) = f(x2), непременно выполняется x1 = x2.
Другими словами, сюръекция — это когда «у каждого образа есть прообраз», а инъекция — это когда «разные — в разные». То есть, при инъекции не бывает так, чтобы два или больше разных элементов X отображались в один и тот же элемент Y. А при сюръекции не бывает так, чтобы какой-то элемент Y не имел прообраза.
2.Функция f называется сюръективной (или, коротко, сюръекция), если каждому элементу множества прибытия может быть сопоставлен хотя бы один элемент области определения. Другими словами, функция f сюръективна, если образ множества X при отображении совпадает с множеством Y: f[X] = Y.
Такое отображение называется ещё отображением на.
Если условие сюръективности нарушается, то такое отображение называют отображением в.
3.Если функция является и сюръективной, и инъективной, то такую функцию называют биективной или взаимно однозначной.
|
24 Алгоритм построения эйлерова цикла.
Цикл называется эйлеровым, если ему принадлежат все ребра (и ни по одному ребру нельзя пройти дважды)
выбрать произвол вел-ну а
выбрать произвольно некоторое ребро, инцидентное а, и присвоить ему №1
каждое пройденное ребро вычеркивать и присваивать ему номер, на единицу больший номера предыдущего ребра
находясь в некоторой вер-не х, не выбирать ребра, инцидентного а, если есть возможность другого выбора
находясь в вер-не х, не выбирать мостов
После того, как все ребра занумерованы ={1,2,…,n} – есть путь, образующий эйлеров цикл.
|
|
|
|
 Скачать 3.85 Mb.
Скачать 3.85 Mb.