18. Метод математической индукции

• Название: 18. Метод математической индукции
• Анкор: DISKRETKA_ShPORY_end.doc
• Дата: 25.04.2017
• Размер: 3.85 Mb.
• Имя файла: DISKRETKA_ShPORY_end.doc
• Тип: Документы; #4841
• страница: 3 из 4

7. Декартово пр-ние мн-в и его св-ва. Геометр интерпретация декарт пр-ний.

Декартовым или прямым пр-нием мн-в А и В называют мн-во АВ всех упорядоченных пар эл-тов (a,b), где aA, bB, т.е. АВ=С=. Эл-ты a и b называют при этом компонентами или координатами пары (a,b). Соответственно, a называют 1ой координатой пары, а b – 2ой корд-той пары.

Если одно из мн-в А или В пусто, то произв-нием АВ будет пустое мн-во.

Известным примером явл-ся мн-во декартовых координат в прямоугольной сис-ме корд-т.

Св-ва декартова пр-ния:

1. 
   декартово пр-ние не коммутативно: АВВА
   
2. 
   декартово пр-ние не ассоциативно: ((АВ)С)(А(ВС)).
   

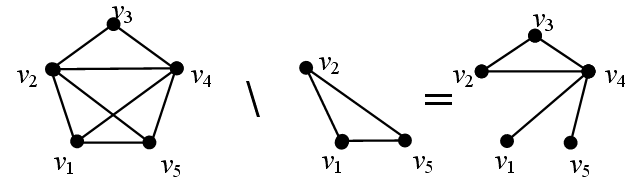
Для док-ва этих фактов достаточно привести примеры, когда коммутативность и ассоциативность не выполняются:

Пример 1. Пусть A={1}, В={2,3}, тогда АВ={(1,2),(1,3)}, BA={(2,1),(3,1)}. Обратим внимание, что в случае, когда А=В, переместительный закон имеет место.

Пример 2. Пусть A={1}, B={2}, C={3}, тогда ((AB)C)={(1,2),3}, т.е. декартово пр-ние состоит из одной пары, 1ая коорд-та которой есть пара (1,2), а 2ая – эл-т 3. В то же время (A(BC))={1,(2,3)}, т.е. декартово пр-ние состоит из одной пары, 1ой коорд-той которой явл число 1, а 2ой – пара (2,3)

Декартовым произведением явл плоскость. Например, А=[0,1] и В=[1,2), тогда АВ:

Если А=В, то АВ =А². Если одно из множеств является , то АВ=

21. Компоненты связности, мосты. Критерий моста.

Граф G наз связным, если для любых 2-х его вершин сущ путь, связ-й их, иначе граф наз несвязным.  несвязн граф распад-ся на связные подграфы,кажд из кот явл компонентой связности. Компонента связности – максимально связный подграф.

Подграфом G1=(V1, А1) графа G=(V, А) наз часть графа, кот сама явл графом.

G=(V, А). Пусть V1 V и А1 А ; G1=(V1,А1). G1 явл подграфомдля  (Xi, Xj)А1

 верш, инцид ему и  V1. Несвязный граф облад. таким св-вом, что люб. верш. не связана ни с одной верш. другой компоненты никаким путем.

Мостом наз такое ребро, при удалении кот-го число комп. связности увел-ся.

Т(критерий моста): Ребро графа G явл мостом  оно не  ни 1 из циклов.

Док-во => от противного. Предпол. что сущ цикл, кот  ребро (Хi,Хj) явл. мостом. При удал. (Хi,Хj) число комп. связн. увелич. (по опр. моста), и  для Хk, Хn из разных комп-т нет пути, их соединяющего, а до удал. (Хi,Хj) путь был,  содержал (Хi,Хj) и имел путь: {(Xк, Xк+1)…(Xi,Xj)… (Xn-1, Xn)}).  заменив (Хi,Хj) на обходной путь (т.к. ребро  циклу) получ новый путь из Хk в Хn. Получ. противоречие.

Док-во <= Предполож, что  такое ребро (Хi,Хj), кот не явл-ся мостом и не  ни одному из циклов. Тогда удалим (Хi,Хj). Т.к. (Хi,Хj) – не мост, то число компонент связности не изменилось,   путь из Хi в Хj {Xi,Xi+1,…Xj-1,Xj}. Восстановив ребро (Хi,Хj) получ. цикл. Противоречие. Ч.т.д.

8. Понятие бинарного отношения, способы задания отношений интерпритация графа, как бин отн-гий, задание графа с помощью матрицы

Отношение – бинарное отношение – любое подмножество вида АА.

Пусть A=R, в этом случае отношение “<” означает множество пар декартовой плоскости, расположенное левее биссектрисы 1 и 3 координатных углов.

пример

А{123456}, R{(ai;aj)(ai:.aj)}

	1	2	3	4	5	6
1	1	0	0	0	0	0
2	1	1	0	0	0	0
3	1	0	1	0	0	0
4	1	1	0	1	0	0
5	1	0	0	0	1	0
6	1	1	1	0	0	1

8. св-ва бинарных отношений: рефлексивность, симметричность, интисимметричность, транзитивность.

Свойства:

1. 
   R – рефлексивно, если а: (а;а)R
   

Тогда в матрице отношения R на главной диагонали стоят только единицы: i c_ii=1

2. 
   R – не рефлексивно, если а: (а;а)R
   

На главной диагонали матрицы есть хотя бы один ноль.

3. 
   R – антирефлексивно, если а: (а;а)R
   

Тогда на главной диагонали матрицы стоят только нули: i c_ii=0.

4. 
   R – симметрично, если а,b: (a;b)R  (b;a)R.
   

Тогда в матрице отношения i,j: c_ij=с_ji=1_. Значит, матрица симметрична относительно главной диагонали.

5. 
   R – не симметрично, если a,b: (a;b)R и (b;a)R
   
6. 
   R – антисимметрично, если ab. (a;b)R  (b;a)R, т.е. ни для каких различных a и b (ab) не выполняется одновременно (a;b)R и (b;a)R. Если же (a;b)R и (b;a)R, то a=b. Тогда в соответствующей матрице отношения ни для каких i,j: ij не выполняется Cij=Cji=1. Таким образом, отсутствуют единицы, симметричные относительно главной диагонали.
   
7. 
   R – транзитивно, если того, что a,b,c: (a,b)R и (b,c)R следует, что (a,c)R.
   

В матрице такого отношения должно выполняться след условие: если c_ij=1 и c_jk=1 i, j, k

Говорят, что в М задано бинарное отношение Т, если ММ есть декартово произведение и в ММ выделено произвольное подмн-во Т. Таким образом, произвольное подмн-во ТММ есть бинарное отношение.

Мы будем говорить, что эл-т a находится в отношении Т к эл-ту b в том и только в том случае, когда пара (а,b) принадлежит мн-ву Т. Для этого возможны два равносильных способа обозначения: аТb или (а,b)Т.

21. Понятие подграфа. Реберно-порожденный подграф. Основные операции над графами.

Подграфом G1=(V1, А1) графа G =(V, А) наз часть графа, кот сама явл графом. G =(V, А). Пусть V1 V и А1 А; G1=(V1, А1). G1 явл подграфомдля  (Xi, Xj)А1  верш, инцид ему и  V1

Граф G1=(V1, А1) наз реберно-порожд. подграфом графа G, когда V1 содержит все вершины графа G, инцидентные ребрам из А1.

Операции над графами:

1) Объединение двух графов G1=(V1, A1) и G2=(V2, A2) есть граф S=(V1V1,A1A2).На рисунке 1 показано объединение двух графов.

2) Пересеч. двух графов G1=(V1, A1) и G2=(V2,A2) есть граф S=(V1∩V2,A1∩A2).

3) Кольцевая сумма двух графов G1G2 есть граф, не имеющий изолированных вершин и состоящий только из ребер, присутствующих либо в G1, либо в G2, но не в обоих графах одновременно. Т.о. это Е1Е2 реберно-порожденный граф. G1G2=(G1 \ G2)(G2 \ G1)

4) Разностью графов G1=(V1, А1) и G2=(V2, А2) наз-ся граф G =(V, А) где А=А1 А2 и G явл реберно-порожд. подграфом графа G1.

5) Дополнение графа G наз-ся граф G1 с теми же вершинами, что и граф G и с ребрами, кот-е надо добавить к графу G чтобы получить полный граф. Полный граф – все его вершины смежны между собой.

9. Отношение эквивалентности, определения, примеры. Теоремы о связи разбиения множества и отношением эквивалентности на нем

Бинарное отношение ТММ называется отношением эквивалентности, заданном на мн-ве М, тогда и только тогда, когда оно удовлетворяет следующим трем усл-виям:

a, aM  (a,a)T, т.е. отношение Т удовлетворяет усл-вию рефлексивности

ab, aM, bM если (a,b)T, то (b,a)T, т.е. отношение Т удовлетворяет усл-вию симметричности

abc, aM, bM, cM если (a,b)T и (b,c)T, то (a,c)T, т.е. отношение Т удовлетворяет усл-вию транзитивности

Таким образом, эквивалентность есть бинарное отношение, удовлетворяющее усл-виям рефлексивности, симметричности и транзитивности.

Отношение равенства чисел есть отношение эквивалентности, т.к. является рефлексивным, симметричным и транзитивным.

А бинарное отношение «<» для чисел не явл отношением эквивалентности, т.к. оно не удовлетворяет условию симетричности.

Разбиение множества. Пусть А — произвольное множество. Семейство  непустых и попарно не пересекающихся множеств называют разбиением множества А, если объединение множеств семейства  равно А, то есть

 Для любого отношения эквивалентности на множестве А множество классов эквивалентности образует разбиение множества А. Обратно, любое разбиение множества А задает на нем отношение эквивалентности, для которого классы эквивалентности совпадают с элементами разбиения.

отношение эквивалентности P на множестве A определяет некоторое разбиение этого множества. Убедимся вначале, что любые два класса эквивалентности по отношению P либо не пересекаются, либо совпадают.
Пусть два класса эквивалентности [X]p  и [Y]p имеют общий элемент . Тогда  и . В силу симметричности отношения P имеем , и тогда  и . В силу транзитивности отношения P получим X P Y. Пусть , тогда . Так как , то  и, следовательно, .

Обратно, если , то в силу симметричности  получим  и в силу транзитивности — , то есть . Таким образом, .

Итак, любые два не совпадающих класса эквивалентности не пересекаются. Так как для любого  справедливо  (поскольку ), т.е. каждый элемент множества A принадлежит некоторому классу эквивалентности по отношению P, то множество всех классов эквивалентности по отношению P образует разбиение исходного множества A. Таким образом, любое отношение эквивалентности однозначно определяет некоторое разбиение.

Теперь пусть  — некоторое разбиение множества . Рассмотрим отношение P, такое, что  имеет место тогда и только тогда, когда X и Yпринадлежат одному и тому же элементу  данного разбиения:

Очевидно, что введенное отношение рефлексивно и симметрично. Если для любых  и  имеет место  и , то  и  в силу определения отношения  принадлежат одному и тому же элементу  разбиения. Следовательно,  и отношение P транзитивно. Таким образом, P — эквивалентность на A.


31Отношения нестрогого порядка, определения, примеры.

Говорят, что отношение нестрогого порядка задано на мн-ве М, если Т есть бинарное отношение, подчиненное следующим трем усл-виям:

1. 
   а, аМ  (а,а)Т, т.е. отношение Т удовлетворяет условию рефлексивности
   
2. 
   ab, aМ, bМ, если (a,b)Т и (b,a)Т, то a=b, т.е. отношение Т удовлетворяет условию антисимметричности
   
3. 
   abc, aМ, bМ, cМ, если (a,b)Т и (b,c)Т, то (a,c)Т, т.е. отношение Т удовлетворяет условию транзитивности
   

Таким образом, отношение нестрогого порядка есть бинарное отношение, удовлетворяющее усл-виям рефлексивности, антисимметричности и транзитивности.

Пример 1. Отношение «» для чисел есть отношение нестрогого порядка. Действительно, для любых действительных чисел a,b,c выполняются все три условия: аа; если аb и ba, то a=b; если ab и bc, то ac.

Пример 2. Отношение «быть подмн-вом» также явл отношением нестрогого порядка, т.к. любое мн-во явл подмн-вом самого себя, а также, если АВ и ВА, то А=В, и, наконец, если АВ и ВС, то АС.

Отношения строгого порядка, определения, примеры.

Говорят, что на мн-ве М задано отношение строгого порядка Т, если есть бинарное отношение, подчиненное следующим трем усл-виям:

1. 
   a, aM  (a,a)T, т.е. отношение Т удовлетворяет усл-вию антирефлексивности
   
2. 
   ab, (a,b) и (b,a) не могут принадлежать Т одновременно, т.е. отношение Т удовлетворяет усл-вию несимметричности
   
3. 
   abc, aM, bM, cM если (a,b)T и (b,c)T, то (a,c)T, т.е. отношение Т удовлетворяет усл-вию транзитивности
   

Таким образом, отношение строгого порядка есть бинарное отношение, удовлетворяющее усл-виям антирефлексивности, несимметричности и транзитивности.

Пример 1. Отн-е «<» для чисел есть отн-е строг порядка. Так, про любое действит число a нельзя сказать, что a
Пример 2. Отн-е между людьми «один старше др» также явл отн-ем строгого порядка.