18. Метод математической индукции.
В математике при доказательстве утверждений часто используется метод математической индукции. Индукция бывает полной и неполной.
Неполная математическая индукция возможно только в том случае, если осуществим полный перебор. Иначе применяют принцип полной математической индукции.
Неполная индукция. Например: n, 2≤n≤15, что n явл простым или пр-нием не более 3х простых чисел; док-во: 2 – прост, 3 – прост, 4=22, 5 – прост, 6=23, 7 – прост, 8=222, 9=333 и т.д.
Полная индукция:
1. база индукции (проверка предположения)
Ф(1) – проверяем истинность утверждения при n=1
2. индукционное предположение
Ф(к) – предпожим, что утверждение истино при n=k
3. индукционный шаг
Ф(к)Ф(к+1). Докажем, что из истинности предполож-я при n=k истинность при n=k+1
4. индукционный вывод
Т.к. предполож. истинно при n=1 а из истинности при n=k истинность при n=k+1истинно при n=2,3,4… истинно для n
|
14. Декарт пр-ние n мн-в, n-арные отн-ния, классич операции над отношениями.
Кортеж или n-ка – посл-ть эл-тов, т.е. мн-во, в котором каждый эл-т занимает определенное место. Обозначается кортеж как: (a1,a2,…,an), а a1,a2,…,an суть его эл-ты, которые называются компонентами кортежа, их число – длина кортежа.
Декар пр-ние A1A2…An мн-в A1,A2,…,An представляет собой мн-во всех упоряд n-к эл-тов (a1,a2,…,an), где a1A1, a2A2, …, anAn. В этом случае а1 назыв 1ой корд-той и т.д.
В частности, декартово пр-ние RRR, где R – мн-во действительных чисел, определяет трехмерное геометрич пр-во, где эл-ты a=(x,y,z) явл точками трехмер евклидового пр-ва.
N-арным (или n-местным) отношением называется любое подмн-во Т декартова пр-ния n-й степени: TMn. Точками отношения T являются посл-ти вида (a1,a2,…,an), где aiM.
Для n-арных отношений операции вводятся аналогично бинарным отношениям.
Таким образом, если T и S суть n-местные отношения в мн-ве M, то n-местными отношениями в М будут также следующие подмн-ва: TS, TS,  =M\T, T\S, TS. =M\T, T\S, TS.
|
1. Понятие множества, подмножества, пустого множества. Диаграммы Венна.
Мн-во – неопределенное понятие, которое характеризуют перечисление его свойств.
Подмн-во А мн-ва В – мн-во, состоящее из элементов, обладающих следующим св-вом:  , т.е. АВ. Если мн-во А явл. подмн-вом В и мн-во В явл подмн-вом А, то А=В. Если мн-во А явл подмн-вом В и при этом они не равны, то мн-во А называют собственным подмн-вом мн-ва В. , т.е. АВ. Если мн-во А явл. подмн-вом В и мн-во В явл подмн-вом А, то А=В. Если мн-во А явл подмн-вом В и при этом они не равны, то мн-во А называют собственным подмн-вом мн-ва В.
Мн-во, которое не содержит эл-тов, называется пустым мн-вом и обозначается символом .
Диаграммы Венна —инструмент, позволяющий изображать множества и иллюстрировать операции над ними. Множества в диаграммах Венна изображаются внутренними частями кругов, их пересечениями, объединениями и
т.д. Прямоугольник изображает универсальное множество.
Рисунки вида  называются диаграммами Венна. Они графически отображают множества. называются диаграммами Венна. Они графически отображают множества.
|
15. Реляционные операции над отн-ми: операции выбора, проекции и соединения.
В реляционных операциях рассматриваются только одноэлементные отношения.
Пусть Т – отношение над множеством А со схемой отношений М={M1,M2,…Mn }.
А) Выбор по атрибуту Мi со значением а осуществляется следующим образом: те стоки, в которых в i-ом столбце нет элемента а, вычёркивается.
Свойства операции выбора:
Операция выбора является унарной операцией
Она не меняет схемы отношений ( и следовательно его формата)
При применении операции выбора арность не увеличивается
σ Мi=b (σ Мi=a (T))= σ Мi=a(σ Мi=b (T)) i j ij
Операция обобщённого выбора:
σ mx(T) осуществляется выбором тех строк, у которых значение атрибута Мi линий в выбранном подмножестве х, при этом остальные строки зачёркиваются.
Б) операция проекции хR(T) (где R – схема отношения) осуществляется выбором столбцов, принадлежащих х, при этом остальные столбцы вычёркиваются и при этом из одинаковых строк остаётся лишь одна. Таким образом формат отношения при операции проекции уменьшается, а не увеличивается.
В) Операция соединения – бинарная операция, т.е. она применяется к 2 отношениям и в результате получаем новое отношение. Оно обозначается T►◄S. Пусть схема отношения Т равна R1, а схема отношения S равна R2, тогда схема отношения T►◄S есть R=R1UR2.
Соед-ем отн-ний T и S будет мн-во таких картежей q, что для q существует два картежа qT и qS, что если вычеркнем из картежа q атрибуты, не входящие в Т, то получим картеж qT, а если вычеркнем из картежа q атрибуты. Не входящие в S, то получим картеж qS.
|
2. Оп-ции об-ния, перес-ния мн-в, опр-ние и св-ва ком-ти и ассоц-ти.
Объединением 2х мн-в А и В называется мн-во С, состоящее из всех элементов, принадлежащих хотя бы одному из мн-в А и В, т.е. АВ=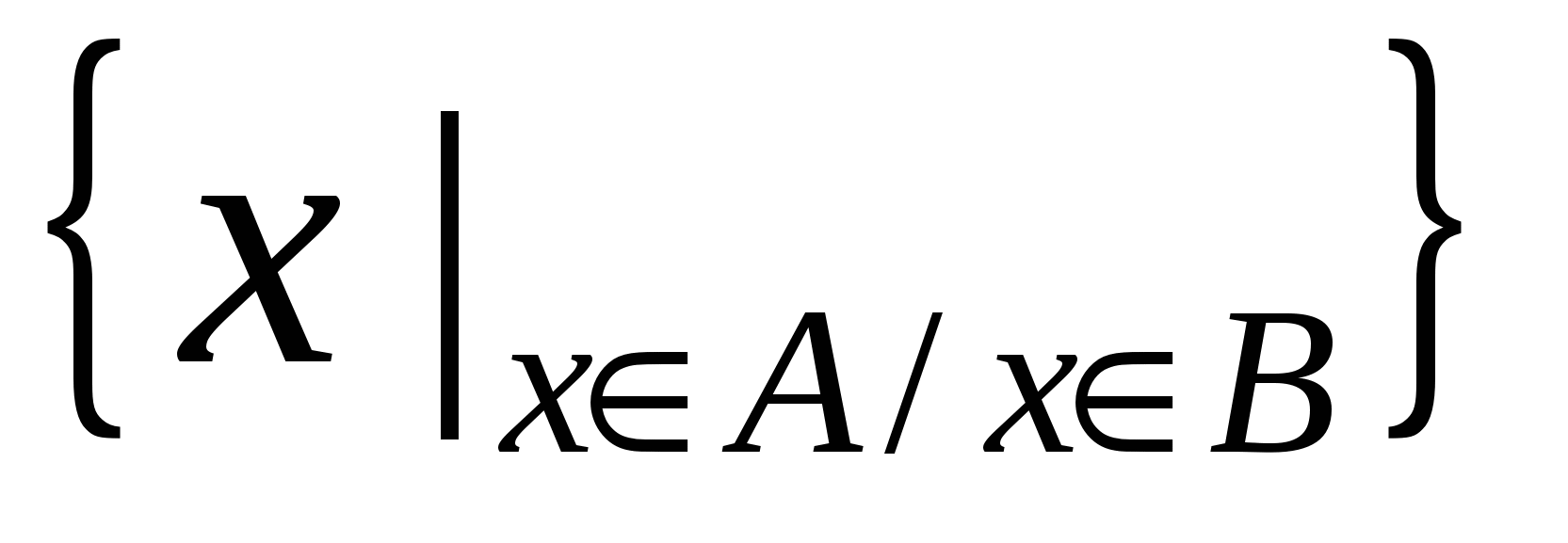
Пересечением 2х мн А и В наз-ся мн С, сост из всех эл-тов, принадл-их как мн А, так и мн-ву В, т.е. АВ= . мн А и В не имеют общ эл-тов их перес-ем явл пуст мн. . мн А и В не имеют общ эл-тов их перес-ем явл пуст мн.
Аналогично определяется об-ние и перес-ние любого (конеч или бесконеч) числа мн-в. Если Ai – произвол мн-ва, то их сумма (объединение) А – есть совокупность элементов, каждый из которых принадлежит хотя бы одному из мн-в Ai. Это обозначается  . .
Пересечением любого (конеч или бесконеч) числа мн-в Ai называется совокупность А элементов, принадлежащих каждому из мн-в Ai. Это обозначается 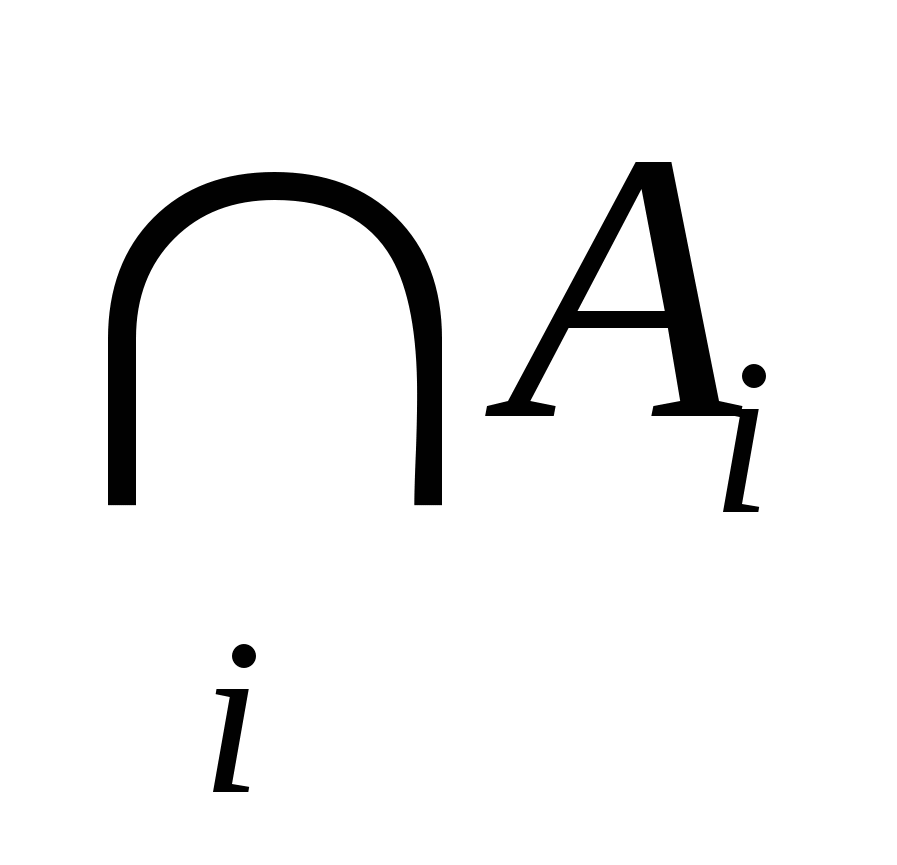 . .
Оп-ции объед-ния и перес-ния ком-ны, т.е. для них выполняется переместит закон:
АВ=ВА АВ=ВА
Также эти операции ассоциативны, т.е. для них выполняется сочетательный закон:
(АВ)С=А(ВС) (АВ)С=А(ВС)
Эти св-ва операций следуют из их определения.
Взаимная дистрибутивность операций пересечения и объединения.
Операции пересечения и объединения взаимно дистрибутивны, т.е. для них выполняется распределительный закон:
(АВ)С=(АС)(ВС) (1)
(АВ)С=(АС)(ВС) (2)
Док-ва этих теоретико-множественных равенств проводятся в обе стороны, т.е. для док-ва того, что А=В, показывают, что с одной стороны АВ, а с другой стороны АВ.
Док-во (1). (АВ)С (АС)(ВС), x, x(АВ)С xA или хВ и хС (хА и хС) или (хВ и хС) хАС или х ВС х(АС)(ВС); (АВ)С (АС)(ВС) док-ся аналогично, все стрелки можно обернуть.
Док-во (2). (АВ)С (АС)(ВС), x, x(АВ)С xA и хВ или хС (хА или хС) и (хВ или хС) хАС и х ВС х(АС)(ВС); (АВ)С (АС)(ВС) док-ся аналогично, все стрелки можно обернуть.
|
12.Логика высказ. Лог связки. Ф-лы логики высказ. Подформула, Ранг формулы.
Логика высказываний — это формальная теория, основным объектом которой служит понятие логического высказывания. Несмотря на свою важность и широкую сферу применения, логика высказываний является простейшей логикой и имеет очень ограниченные средства для исследования суждений
Высказыванием наз повеств предложение, про кот. можно сказать истинно оно или ложно.
Определение. Формулами логики высказываний называются выражения вида (F)^(G), (F) ˅ (G), не(F), (F)-> (G), (F)<>(G)
Подформулой формулы А называется любое подслово А, само являющееся формулой.
Например, формула F=X&Y->X˅Z имеет шесть подформул: X,Y,Z,X&Y, X˅Z, X&Y->X˅Z.
Ранг – это число высказывательных операций.
Логические операции:
Отрицанием высказывания А наз такое высказывание, к-рое истинно, когда А-ложно и ложно, когда А-истинно. А – «не А».
Конъюнкцией высказываний А и В наз высказывание, к-рое истинно, когда А-истинно и В-истинно и ложно во всех ост случаях. A&B, AB, AB – «А и В».
Дизъюнкцией высказываний А и В наз высказывание, к-рое ложно, когда А-ложно и В-ложно и истинно во всех ост случаях. АВ, А+В – «А или В».
Импликацией высказываний А и В наз высказывание, к-рое ложно, когда А-истинно, а В-ложно и истинно во всех ост случаях. АВ, АВ – «из А следует В».
Эквиваленцией высказываний А и В наз высказывание, к-рое истинно, когда А и В принимают одинаковое значение и ложно во всех ост случаях. АВ, АВ – «А эквивалент В».
Штрих Шеффера, обычно обозначаемый |, эквивалентен операции И-НЕ и задаётся следующей таблицей истинности:равен нулю только при 11.
С  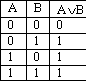   трелка Пирса, обычно обозначаемая ↓, эквивалентна операции ИЛИ-НЕ и задаётся следующей таблицей истинности: равно единице только при 00. трелка Пирса, обычно обозначаемая ↓, эквивалентна операции ИЛИ-НЕ и задаётся следующей таблицей истинности: равно единице только при 00.
|
3. Операция вычитания мн-в, отсутствие коммутативности и ассоциативности.
Разностью 2х мн-в А и В называется совокупность тех эл-тов мн-ва А, кот. не содер-ся в мн-ве В, т.е. С=А\В={x | xA, x не В }. В не может быть подмн-вом мн-ва А. Операция вычитания некоммутативная и неассоциативная, подобно операции вычитания чисел в арифметике. Если отсутствие коммутативности практически очевидно: 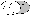 и и  , то отсутствие ассоциативности нуждается в док-ве. Покажем, что (А\В)\СА\(В\С). Мн-во, стоящее в лев части, состоит из эл-тов мн-ва А, не являющихся при этом эл-тами ни мн-ва В, ни мн-ва С, т.е. совпадает со мн-вом А\(ВС) , то отсутствие ассоциативности нуждается в док-ве. Покажем, что (А\В)\СА\(В\С). Мн-во, стоящее в лев части, состоит из эл-тов мн-ва А, не являющихся при этом эл-тами ни мн-ва В, ни мн-ва С, т.е. совпадает со мн-вом А\(ВС)  . Мн-во, стоящее в прав части, состоит из эл-тов мн-ва А, не являющихся при этом эл-тами мн-ва В, но при этом эл-ты, являющиеся пересечением мн-в А, В и С, входят в это мн-во, т.е. это мн-во совпадает с мн-вом А\В(АВС) . Мн-во, стоящее в прав части, состоит из эл-тов мн-ва А, не являющихся при этом эл-тами мн-ва В, но при этом эл-ты, являющиеся пересечением мн-в А, В и С, входят в это мн-во, т.е. это мн-во совпадает с мн-вом А\В(АВС)  . .
|
13.Таблица истинности. Равносильность формул. Тавтологии.
Две формулы алгебры логики A и B называются равносильными, если они принимают одинаковые логические значения при любом наборе значений входящих в формулы элементарных высказываний (переменных).
Обозначение. A≡B. Пример . . .
Ф-ла наз ТИ-высказыванием (или тавтологией) она принимает значение «1» набора выск-х переменных. Ф-ла наз ТЛ-высказыванием она принимает значение «0» набора выск-х переменных.
Ф-ла наз выполнимой набор выск-х переменных, при к-ром она принимает значение «1». Ф-ла наз невыполнимой она принимает значение «0» набора выск-х переменных.
Основные равносильности.
 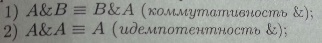 
|
4. Симметрическая разность, определения и св-ва.
Симметрической разностью 2х мн-в А и В называется сумма разностей А\В и В\А  , т.е. С=АВ=(А\В)(В\А). Заметим, что АВ=(АВ)\(АВ), т.к. симметрическая разность состоит из тех эл-тов мн-в А и В, которые не принадлежат А и В одновременно. , т.е. С=АВ=(А\В)(В\А). Заметим, что АВ=(АВ)\(АВ), т.к. симметрическая разность состоит из тех эл-тов мн-в А и В, которые не принадлежат А и В одновременно.
Док-во: АВ (АВ) \ (АВ), x, x(А\В)(В\А) xA\B или хВ\А (хА и хВ) или (хВ и хА) 1) хА и хАВ, 2) хВ и хАВ х(АВ)\(АВ); в обратную сторону аналогично.
Операция является и коммутативной, и ассоциативной: АВ=ВА, (АВ)С=А(ВС).
|
5. Операция дополнения мн-в, принцип двойственности.
Дополнением к мн-ву А является мн-во  (не А), которое дополняет мн-во А до универсума (основного мн-ва S), т.е. (не А), которое дополняет мн-во А до универсума (основного мн-ва S), т.е.  . .
Принцип двойственности для 2х мн-в:
1) 
2) 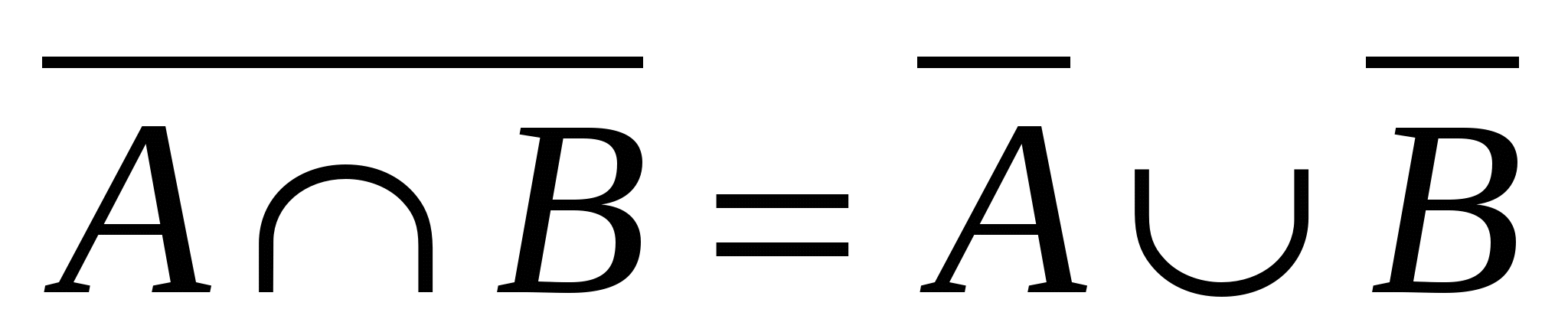
Док-во (2): 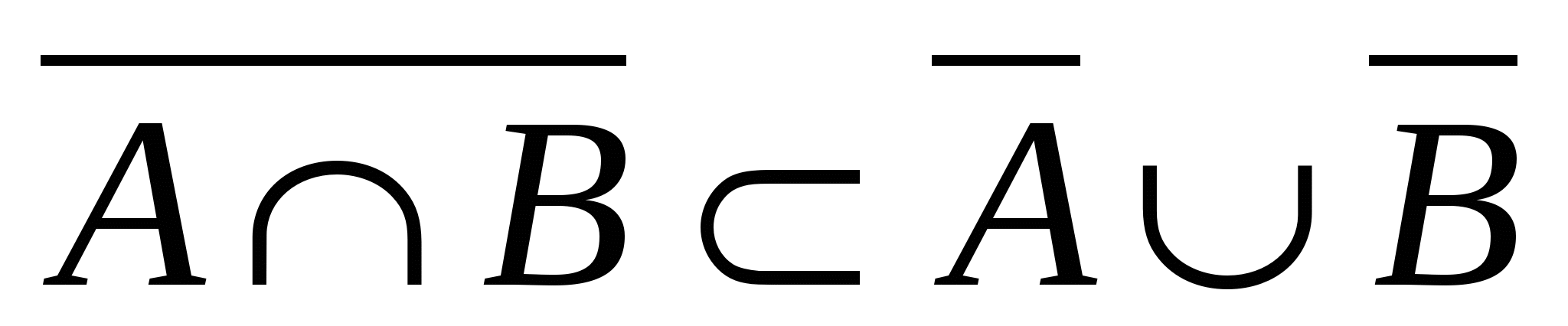 , х, х , х, х хАВ х А и В одновременно хА или хВ х хАВ х А и В одновременно хА или хВ х или х или х х х 
Док-во (1) аналогично.
Принцип двойств-ти состоит в том, что из люб рав-ва, состоящего из с-м подмн-в осн мн-ва С, может быть получено двойственное рав-во путем замены кажд рассматриваемого мн-ва его дополнением, объединений мн-в – их пересечениями, а пересечений – объединениями.
|



Принцип двойственности

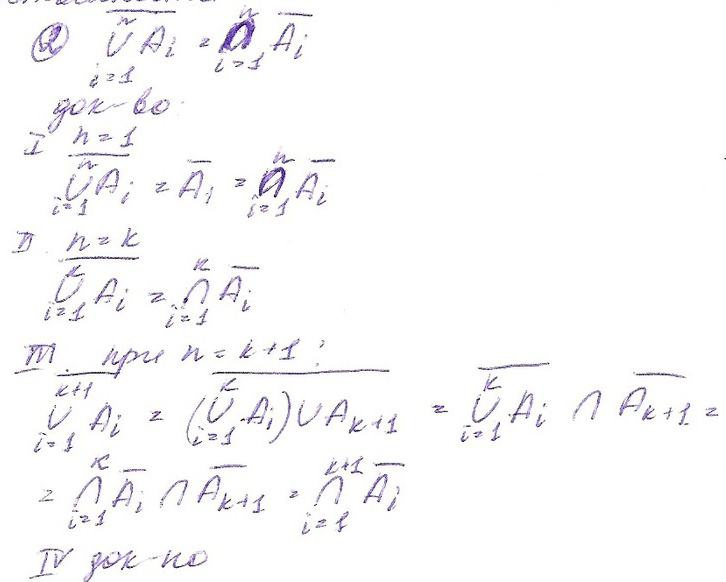
|
14. Полные и не полные системы пропозициональных операций примеры с док-ом Теорема о приведенной форме ( с доказательством).
14 Полные и неполные системы пропозициональных операций. Примеры полных и неплоных систем(с док-вом) Теорема о приведенной форме
Def Формула имеет приведенную форму она не содержит импликаций(->) и эквиваленций,а знак отрицания может стоять только над высшей переменной.
Теорема о приведенной форме:
Любая формула эквивалента некоторой приведенной форме.
Док-во
Из 16) (A->B)(-A\/B)=>импликация может быть устранена
Из 19) (AB)((-A\/B)/\(A\/-B))=>эквивваленция также может быть устранена
Пользуясь законами де Моргана,постепенно снимаем отрицание с подформул,пока оно не будет стоять над высказывательной переменной.
Система высказывательных переменных назыв. Полной если любая формула эквивалента некоторой формуле,в которую входят высказывательные операции(Базис). В этом случае говорят, что система высказ-х операция обретает базис
Теорема системы операций
< --, /\, \/> явл. Полным (образуют базис)
Док-во
< --, /\, \/>,т.к из 16,19 законов устраняются импликация и эквивалентность
< --, \/> т.к (A/\B) --(-A\/-B) => устраняется /\
Утверждение системы < /\, \/> не явл. Полным
Док-во
Если формула А зависит от выск.переменных
А(х1,х2,х3…хn) и все выск-е переменные системы имеют значение 1, то А(x1,x2…xn)=1 из ТИ /\ и \/
А в формуле,содержащей отрицание может получиться 0, то и все х1,х2,..хn имеют значение 1
Например, х1 -x2
| |
 Скачать 3.85 Mb.
Скачать 3.85 Mb.