18. Метод математической индукции
 Скачать 3.85 Mb.
|
=> Эта формула не может быть выражена без -- . х\/--x=1 Утверждение < -- > не явл.полной системой Док-во: т.кс помощью – могут быть выражены только формулы,содержащие выск.переменную Существуют операции,образующие полную систему. Одна из них штрих Шеффера,а другая стрелка Пирса Ф-ла наз приведенной она не содержит импликации и эквиваленции, а отрицание может стоять только над высказ-й переменной. Теорема. ф-лы А эквивалентная ей приведенная ф-ла. Док-во: 1)избавляемся от всех и по 16 и 19 законам. Получили А А 2)докажем теорему индукцией по rank(A’) I база индукции: r(A’)=0 => A'=Xi – высказ переменная явл приведенной. II индукц предположение: предположим, что утвержд теоремы истинно A’ rank(A’)<=k III индукц шаг: док-м, что из истинности т-мы при rang(A’)<=k => истинность т-мы при при rang(A’)=k+1 Возможны случаи: A’=B, A’=B&C, A’=BvC, (rank(B)<=k и rank(С)<=k) по инд-му предположению B и C суть приведенной ф-лы (B&C), (BvC) – прив-е ф-лы. Док-м случай A’=B => rank(B)=k => к B применимо индукц предположение. B=C => C – высказ переменная B=Xi => A’=B=Xi =Xi – приведен. B=C&D, B=CvD => A=B= (C&D) = C v D rank(A)=k+1, rank(B)=k B=C&D =>rank(C)<=k-1, rank(D)<=k-1 => rang(C)=k, rank(D)=k => к C и D применимо инд-е предположение => C и D – м.б.приведенные => C v D - также приведенные. |   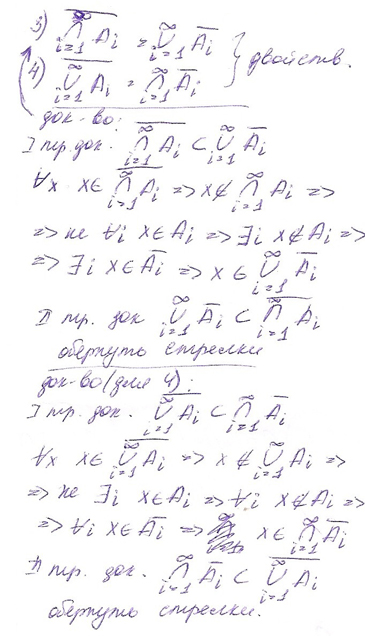 | 15.Элементарные конъюнкции и дизъюнкции. Теоремы о тождественной истинности элементарной дизъюнкции и тождественной лжи элементарной конъюнкции. Элементарной дизъюнкцией называется дизция высказывательных переменных или их отрицаний . Элементарной конъюнкцией называется конция высказывательных переменных или их отрицаний . Элементарная дизъюнкция является тождественно истинным высказыванием(принимает значении 0 при любом наборе высказывательных переменных)она наряду с некоторой высказывательной переменным содержит её отрицание <= очевидно . =>от противного ;предположим ,что существует элементарная дизъюнкция, у которой не существует высказывательных переменных, входящих в дизъюнкцию вместе со свои отрицанием. Придадим значение «0» тем выск. Переменным ,которая входит без отрицания и «1» тем выс. Переменным, которые входят с отрицанием получаем 0U0U0U0=>элементарная диз-ция не является ТИ-высказыванием. =>от противного ;предположим ,что существует элементарная конъюнкция, у которой не существует высказывательных переменных, входящих в конъюнкцию вместе со свои отрицанием. Придадим значение «0» тем выск. Переменным ,которая входит без отрицания и «1» тем выс. Переменным ,котороые входят с отрицанием получаем 0U0U0=>элементарная конция не является ТИ-высказыванием. Теорема1.Для того ,чтобы элементарная дизъюнкция была тождественно истинной, необходимо и достаточно ,чтобы в ней содержалась переменная и ее отрицание Для того, чтобы формула алгебры логики А была тождественно истинна, необходимо и достаточно, чтобы любая элементарная дизъюнкция, входящая в КНФ А, содержала переменную и её отрицание. Теорема2.Для того ,чтобы элементарная конъюнкция была тождественно ложной,необходимо и достаточно ,чтобы в ней содержалась переменная и ее отрицание Для того, чтобы формула алгебры логики А была тождественно ложна, необходимо и достаточно, чтобы любая элементарная конъюнкция, входящая в КНФ А, содержала переменную и её отрицание. 16Теоремы о КНФ и ДНФ. КНФ- конъюнкция элементарных дизъюнкций. ДНФ- дизъюнкция элементарных дизъюнкций. Теорема .Любая формула эквивалента некоторой КНФ(ДНФ). По теореме о приведенной форме любая формула эквивалентна приведенной=>считаем формулу приведенной . Доказательство методом математической индукции по рангу приведенной . Ранг – это число высказывательных переменных . I)База r(A)=0 A=xi-КНФ(ДНФ) II)предположим ,Что утверждение истинно при r(A) III)Инд. Шаг ,докажем , что если утв. Теорема истинной при r(A) 1) А = (неВ1), след. В1=х1, т.к. А-приведенная, след. А=(не xi) – КНФ. 2) А = B1/\B2 – КНФ, т.к. B1, B2 – КНФ 3) A=B1\/B2 = (С1/\C2/\...Ce)\/(D1,D2,…Dm) = ((C1\/D1)/\(C1\/D2)/\...(C1\/Dm)/\(C2\/D1)…/\(Ce\/D1)/\(Ce\/D2)…(Ce\/Dm)-КНФ. К формулам В1 и В2 применимо индукционное предположение, значит считаем их КНФ. 17.Полные элементарные конъюнкции и дизъюнкции. Теорема об эквивалентности ПЭК некоторой СДНФ. Полная элементарная конъюнкция – это конъюнкция в которую входит каждая высказывательная переменная системы, либо её отрицание, при этом ровно один раз. Полная элементарная дизъюнкция – это дизъюнкция в которую входит каждая высказывательная переменная системы, либо её отрицание, при этом ровно один раз. Теорема. Всякая элементарная конъюнкция, не являющаяся ТИ высказыванием эквивалентная некоторой СДНФ. Д-во : Пусть X1,Х2,…,Хn=система высказывательных переменных Yi1˅Yi2˅…˅Yik Элементарная конъюнкция, в которую входят k высказывательных переменных или их отрицание ,где k<=n. Не ограничивая общности высказывания, считаем , что одинаковых индексов нет ,т.к. Yij˅YijYij, Yij˅¬Yij=1=>вся конъюнкция оказалась бы ТИ-высказыванием . I)сл. k=n=>Yi1˅…˅Yik-ПЭК→она представляет СДНФ II)сл. k Yi1˅Yi2˅…˅YikYi1˅Yi2˅…˅Yik˅(Ye^¬Ye)(Yi1˅Yi2˅Yik˅Ye)^(Yi1˅Yi2˅…˅Yik˅Ye). Пополн т.о. все всходящие конъюнкции пока в них не войдут все высказывательные переменные сисетмы, получим дизъюнкцию ПЭК, т.е. СДНФ | 6. Разбиение мн-ва, покрытие мн-ва, примеры в математике и информатике. Представление заданного мн-ва в виде объединения системы мн-в, не имеющих попарно общих точек, называется разбиением. Таким образом, если есть мн-во А, такое что  , где для люб Bi и Bj, BiBj=, то с-ма {Bi} есть разбиение мн-ва А . Очевидно, что мн-ва могут обладать различными разбиениями.П  ример. Мн-во цел чисел можно представить в виде об-ния мн-ва чет чисел и мн-ва нечет чисел с одной стороны, а также в виде об-ния мн-ва чисел, кратных трем, мн-ва чисел, имеющих при дел на 3 в остатке 1, и мн-ва чисел, имеющих при делении на 3 в остатке 2.Любое мн-во подмн-в мн-ва А, объединение которых есть мн-во А, называется покрытием мн-ва А. Сл-но, если есть мн-во А, такое что , то система {Bi} есть покрытие мн-ва А  . Таким образом, разбиение есть частный случай покрытия, т.е. это покрытие, в котором мн-ва Вi не пересекаются.Пример. Мн-во натур чисел можно представить в виде об-ния мн-ва нечет чисел, мн-ва чисел, не дел на 3, и мн-ва чисел кратных 6. Очевидно, что эти подмн-ва пересекаются, на пример, число 7 принадлежит и мн-ву нечетных чисел, и мн-ву чисел, не делящихся на 3. | 17.Полные элементарные конъюнкции и дизъюнкции. Теорема об эквивалентности ПЭК некоторой СДНФ. Полная элементарная конъюнкция – это конъюнкция в которую входит каждая высказывательная переменная системы, либо её отрицание, при этом ровно один раз. Полная элементарная дизъюнкция – это дизъюнкция в которую входит каждая высказывательная переменная системы, либо её отрицание, при этом ровно один раз. Теорема. Всякая элементарная конъюнкция, не являющаяся ТИ высказыванием эквивалентная некоторой СДНФ. Д-во : Пусть X1,Х2,…,Хn=система высказывательных переменных Yi1˅Yi2˅…˅Yik Элементарная конъюнкция, в которую входят k высказывательных переменных или их отрицание ,где k<=n. Не ограничивая общности высказывания, считаем , что одинаковых индексов нет ,т.к. Yij˅YijYij, Yij˅¬Yij=1=>вся конъюнкция оказалась бы ТИ-высказыванием . I)сл. k=n=>Yi1˅…˅Yik-ПЭК→она представляет СДНФ II)сл. k Yi1˅Yi2˅…˅YikYi1˅Yi2˅…˅Yik˅(Ye^¬Ye)(Yi1˅Yi2˅Yik˅Ye)^(Yi1˅Yi2˅…˅Yik˅Ye). Пополн т.о. все всходящие конъюнкции пока в них не войдут все высказывательные переменные сисетмы, получим дизъюнкцию ПЭК, т.е. СДНФ 18. Теоремы о СКНФ и о СДНФ. Теорема о СКНФ. Любая формула ^B, не является ТИ-высказыванием, эквивалентным некоторой СКНФ. Док-во. По теореме о КНФ любая формула эквивалентная некоторой КНФ=>считаем, что данная формула А дана в КНФ. Зачеркиваем те элементарные дизъюнкции, которое являются ТИ-высказыванием, т.к. x^1x. По теореме 1 остальные элементарные дизъюнкции эквивалентны некоторой СКНФ. Проведем все элементарные дизъюнкции к СКНФ и получим конъюнкцию ПЭД. Исключив повторяющиеся ПЭД получим СКНФ. Теорема о СДНФ. Любая формула ^B, не является ТИ-высказыванием, эквивалентным некоторой СДНФ. Док-во. По теореме о ДНФ любая формула эквивалентная некоторой ДНФ=>считаем, что данная формула А дана в ДНФ. Зачеркиваем те элементарные конъюнкции, которое являются ТИ-высказыванием, т.к. x^1x. По теореме 1 остальные элементарные конъюнкции эквивалентны некоторой СДНФ. Проведем все элементарные дизъюнкции к СДНФ и получим конъюнкцию ПЭК. Исключив повторяющиеся ПЭК получим СДНФ. | 27-28. Определение слова, подслова, префикса, суффикса, собственного подслова, собственного префикса и суффикса, их свойства. равенства слов, операции приписывания, свойства операции приписывания. Множ-во символов- алфавит; элементы алфавита-буквы def СЛОВО - любая буква есть слово; - если А – слово и В – слово, то АВ – также слово  ;- пустое слово /\ (слово, не содержащее букв) есть слово. Слово В есть подслово слова D, если А С D≡ABC Слово С есть собственное подслово слова А, если сущ-ют такие слова В и D, что А имеет вид ВСD и хотя бы одно В или D не пусто. Сл С называется префиксом сл В С≡АВ Св-ва префикса:
Слово наз собственным префиксом слова С А-префикс С и А≠С Св-ва собственного префикса: Если А и В суть собств префиксы сл С, то А есть собств преф В или В есть собств преф А. Слово А тогда и только тогда есть префикс ВС, когда имеет место одно из двух: А – собственный префикс слова В или А имеет вид ВD, где D – префикс С. Суффиксом(концом) сл С наз сл В А С≡АВ (Сл С-конец сл А, если сл В |А≡ВС) Св-ва суффикса: 1) слово есть суффикс самого себя. (/\ | /\ есть приписыв-е пустого слова и самого себя.) 2) Пустое слово есть суффикс любого слова. (док-во в 1ом св-ве) 3) Если А–суффикс В, а В–суф С, то А–суф С (св-во транзитивности суф). Док-во: если А–суф В, то сл D | B≡DА, т.к. В–суф С, то сл Е |С≡ЕВ, тогда С≡ЕDА и А–суфС. А–собственный суф В, если А – суффикс В и А≠В Св-ва собственного суффикса: 1) Если А и В суть собственные суф сл С, то А есть собств. суф В или В есть собств. суф А. 2) Сл А есть суф ВС когда имеет место 1 из двух: А – собств. суф сл С или А имеет вид DС, где D – суф С. def 2 слова А и В наз. равными в лексикографическом смысле |A|=|B| и i i-ая буква слова А совпадает с i-ой буквой слова B. (Если два слова А и В построены из одинаковых букв, располож. в одинаковом порядке, слова А и В графически равны) Слова строятся с пом. операции приписывания (конкатенации), т.е. к слову А приписывается справа слово В. Св-ва операции приписывания:
| 19. Понятие графа, примеры. Задачи, послужившие основой теории графов (задача о кенигсбергских мостах, задача о четырёх красках). Графом G наз-ся совокупность 2-х мн-в: мн-ва вершин и мн-ва пар вершин, наз-ых ребрами вершин. G =(V, А), где V – мн-во вершин, А – конеч. мн-во ребер. Vj – начало ребра. Vk – его конец. Если пара вершин соедин. 2 и более ребрами, то ребра – кратные. Если ребро нач-ся и закан-ся в одной и той же вершине, то ребро наз-ся петлей. Вершины графа, соедин. 1 ребром, наз-ся смежными. Ребро и любая из 2х его вершин наз-ся инцидентными. Степенью вершины наз-ся число ребер, инцидентных ей. Если вершина имеет степень 1, то она наз-ся висячей, если степень 0 – изолированной. Граф, допус-й кратные ребра– мультиграф. Допускающий кр. ребра и петли– псевдограф. Граф, в котором нет кратных ребер и петель, называется простым. Задача о кенигсбергских мостах (1736 Л. Эйлер) Ж 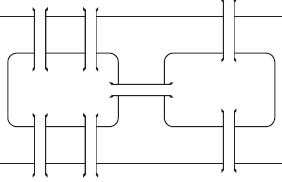 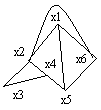 ителям Кен. (Калининград) нрав-сь гулять по дорогам, кот-е включ. семь мостов, соед-х. 2 острова и берега реки Преголя. Люди интерес-сь, могут ли они, начав путь с одного участка суши, обойти все мосты, посетив каждый лишь 1раз, и вернуться в точку начала пути, не переплывая реку. Эйлер построил граф: суша-вершины, а дорожки–ребра.Опираясь на раннее сформулир. и доказаную теор, Эйлер показал, что такого маршрута нельзя построить. Классич. задачи: о 3 домах и 3 колодцах; задача о 4 красках.Зад.о 3 дома и 3кол.. Имеется 3 дома и 3 колодца, располож. на пл-ти. Провести от каждого дома к каждому колодцу тропинку,так, чтобы они не пересекались. Задача была решена (показано, что решения не существует) К Куратовским в 1930. Задача о 4 красках. Разбиение плоскости на непересек-ся области наз-ся картой. Области карты называются соседнимиони имеют общую границу. Задача состоит в раскраш. карты так, чтобы никакие 2 области не были закрашены одним цветом, а теорема состояла в том, что любая карта, не имеющая анклавов (территория, окруж.со всех сторон террит. другого гос-ва) может быть раскрашена 4 красками. | 29 Определение кода. Пусть П={a1,a2,…,am}-алфавит; мн-во слов {b1,b2,…,bn}в этом алфавите наз кодом -й перестанови любого подмнож-ва множ-ва символов {1,2,..,n} не bi1bi2…bik≡bj1bj2…bjl где {i1, i2,..,ik},{j1, j2,..jl}<{1,2,..,n} (Мн-во слов {b1,b2,…,bn} в алфавите П={a1,a2,…,am} называется кодом, если не сущ-ет такой перестановки {i1,i2,…,in} символов {1,2,…,n}, что b1b2…bn=bi1bi2…bin.) B={ab; abb} – код. B={a; b; ab}, (где a=b1, b=b2, ab=b3) – не код, т.к. b1b2b3b3b1b2. Теорема для кодировки -го конечного алфавита код, использующий две буквы. Док-во: пусть используемым алфавитом явл {0;1} i a1 = 0…01, где 0..0 – i раз. Заданное отображение является биекцией | 20. Ориентированный граф, двудольный граф, примеры. Пути и циклы в графах. Критерий простого цикла. 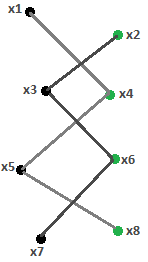 Если пары (Хi,Хj) упорядоч. (не допускается перестановка вершин), то граф наз. ориентированным и пара вершин наз. дугой. Vj – начало ребра. Vk – его конец. Путем наз послед-ть ребер, в кот 2 координата предыдущ. ребра совпад. с 1 коорд. последующ. ребра и ни одно ребро не встречается дважды. Если путь не проходит дважды через 1 и ту же вершину, то он наз простым. Длиной пути наз кол-во ребер в нем. Циклом наз путь, кот. начин. и заканч-ся в 1 и той же верш. Если цикл не проходит дважды через 1 и ту же верш., то он наз простым. Длиной цикла наз кол-во ребер в нем. Т1 (Критерий простого цикла) Чтобы граф G представлял собой простой цикл каждая его вершина имела степень 2. =>Для его вершины Xi в нее 1 раз вошли, и 1 раз вышли => deg(Xi)=2 <=Докажем индукц. по кол-ву вершин. 1 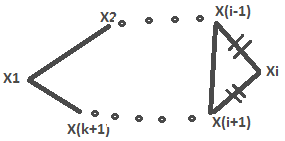 шаг. База инд. 3. При n=3 – верно (рисуем треугольник)2 шаг. Предп-им, что теор верна при кол-ве вершин = k 3 шаг. Док-м что из истин-ти утверж. при n=k след-т истин-ть n=k+1: Для люб. Xi –удалим Xi. Имеем, для люб. j≠i±1 deg(Xj)=2, а для Xi-1 и Xi+1 степень стала равна 1. Соедин. Xi-1 и Xi+1 новым ребром, тогда deg(X i±1)=2 Получ. граф G1, удовлетв. инд. предпол., след-о он представл. собой простой цикл ({X1…Xi-1,Xi+1… Xк+1},{(X1,Х2);(Х2,Х3);…(Xi-1, Xi+1)…(Xк+1,Х1)})- G1 Восстанов. Xi и после восстановл. имеем: ({X1…Xi-1,Xi,Xi+1… Xк+1};{(X1,Х2);(Х2,Х3);…(Xi-1, Xi),(Xi, Xi+1)… … (Xк+1,Х1)}) – простой цикл. 4 шаг. Предл. истин. при n=3, а из истин-ти предл. при n=k след-т истин-ть n=k+1, значит истинно при n=4,5… | |