высшая математика. 2 13 Случайная величина распределена нормально с параметрами 3 и 2(N3,2). Ее математическое ожидание и дисперсия равны mx 3 dx 4
 Скачать 0.84 Mb. Скачать 0.84 Mb.
|
|
экономические процессы и специальные математические методы По степени агрегирования экономических объектов различают макроэкономические Два предпринимателя используют для пошива одежды одинаковую ткань из двух магазинов. Потребность каждого из них соответственно составляет 120 и 190 м. Предложение магазинов 140 и 170 м. Тарифы перевозок (руб.) известны и задаются матрицей 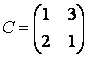 . Целевая функция задачи имеет вид . Целевая функция задачи имеет видПо фактору неопределённости различают модели стохастические, детерминированные Из двух сортов бензина образуются две смеси. Первая состоит из 70% бензина первого сорта и 30% бензина второго сорта; вторая — из 20% бензина первого сорта и 80% второго сорта. Цена первой смеси — 30 у.е., второй — 10 у.е. за тонну. Найти, сколько смеси первого и второго вида можно изготовить из 28 тонн первого сорта и 30 тонн второго сорта, чтобы получить максимальный доход. Система ограничений задачи имеет вид 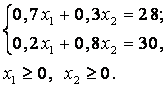 Из двух сортов бензина образуются две смеси. Первая состоит из 70% бензина первого сорта и 30% бензина второго сорта; вторая — из 30% бензина первого сорта и 70% второго сорта. Цена первой смеси — 30 у.е., второй — 10 у.е. за тонну. Сколько смеси первого и второго вида можно изготовить из 28 тонн первого сорта и 30 тонн второго сорта, чтобы получить максимальный доход? Критерием эффективности задачи является функция Математическая модель, содержащая блоки,где в принятии решений может выступать база данных, называется имитационной моделью Состояния экономического объекта в конкретный текущий момент описывают статические модели Совокупность уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических условий, называется … системой ограничений Для минимизации затрат времени на ожидание в очереди создаются модели модели систем массового обслуживания. По типу математического аппарата различают модели корреляционно-регрессионные, теории массового обслуживания Тренд — это длительная тенденция Экзогенными называют независимые переменные Предприятие выполняет 2 проекта. Выходные результаты каждого проекта являются входными данными для следующего проекта. В качестве исполнителей рассматриваются 2 отдела. Время, необходимое каждому для реализации проектов (мес.) приведено в матрице 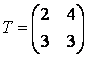 . Считается . Считается 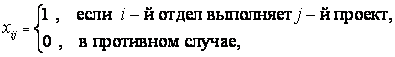 нужно выбрать исполнительский отдел для каждого проекта так, чтобы суммарное время выполнения всех проектов было минимальным. Система ограничений задачи имеет вид нужно выбрать исполнительский отдел для каждого проекта так, чтобы суммарное время выполнения всех проектов было минимальным. Система ограничений задачи имеет вид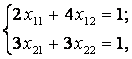 Взаимодействие структурных и функциональных составляющих экономики как предприятия и фирмы описывают модели. Микроэкономические Предприятие изготавливает и продает краску двух видов: для внутренних и внешних работ. Для производства краски используется два исходных продукта A и B. На одну тонну краски для внутренних работ используется 1 т продукта А и 3 т продукта В. Расходы на производство одной тонны краски для внешних работ составляют: 2 т продукта A и 1 т продукта В. Запасы продуктов на складе ограничены (по три тонны продукта А и продукта В). Продажная цена за 1 тонну краски для внутренних работ составляет 2 тыс. рублей, краска для наружных работ продается по 1 тыс. рублей за 1 тонну. Требуется определить, какое количество краски каждого вида следует производить предприятию, чтобы получить максимальный доход. Система ограничений математической модели задачи имеет вид 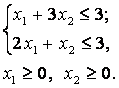 Эндогенными называют зависимые переменные Фирма, обслуживающая туристов, должна разместить их в 4-х отелях: “Морской”, “Солнечный”, “Слава” и “Уютный”, в которых забронировано соответственно 5, 15, 15 и 10 мест. Пятнадцать туристов прибывают по железной дороге, 25 прилетают очередным рейсом в аэропорт, а 5 человек прибудут на теплоходе. Транспортные расходы при перевозке из пунктов прибытия в отели заданы матрицей 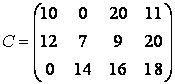 . Требуется определить такой план перевозки туристов из пункта прибытия в отели, при котором суммарные транспортные расходы будут минимальны и все туристы будут размещены в отелях. Правильное ограничение для отеля “Солнечный” имеет вид . Требуется определить такой план перевозки туристов из пункта прибытия в отели, при котором суммарные транспортные расходы будут минимальны и все туристы будут размещены в отелях. Правильное ограничение для отеля “Солнечный” имеет вид По цели создания и применения различают модели эконометрические, балансовые В управлении проектами наиболее широко применяют модели сетевые По степени математической идеализации детерминированные модели подразделяют на линейные и нелинейные Найти из множества возможных (альтернативных) вариантов наилучший вариант производства, распределения или потребления позволяют модели оптимизационные Фирма, обслуживающая туристов, должна разместить их в 4-х отелях: “Морской”, “Солнечный”, “Слава” и “Уютный”, в которых забронировано соответственно 5, 15, 15 и 10 мест. Пятнадцать туристов прибывают по железной дороге, 25 прилетают очередным рейсом в аэропорт, а 5 человек прибудут на теплоходе. Транспортные расходы при перевозке из пунктов прибытия в отели заданы матрицей 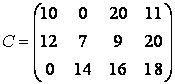 . Требуется определить такой план перевозки туристов из пункта прибытия в отели, при котором суммарные транспортные расходы будут минимальны. Правильное ограничение для вывоза туристов, прибывающих на железнодорожный вокзал имеет вид . Требуется определить такой план перевозки туристов из пункта прибытия в отели, при котором суммарные транспортные расходы будут минимальны. Правильное ограничение для вывоза туристов, прибывающих на железнодорожный вокзал имеет вид Функционирование экономики как единого целогоописывают модели макроэкономические; Вариант, максимальный по обобщенному критерию, если весовые коэффициенты для его составления: a = 0,4 ( ), b = 0,6 ( ), равен 3 Вариант, минимальный по обобщенному критерию, если весовые коэффициенты для его составления: a = 0,4 ( ), b = 0,6 ( ), равен 4 После сужения этого множества при нижних границах , Парето-оптимальное множество примет вид 3 После субоптимизации этого множества по при Парето-оптимальное множество примет вид 3 После лексиографической оптимизации этого множества при Парето-оптимальное множество примет вид 3 В приведенной матрице выигрышей после исключения доминируемых альтернатив, множество сравнимых альтернатив равно (2, 3, 4) Для приведенной матрицы выигрышей множество доминируемых альтернатив равно (1, 5) Оптимальный проект по критерию Лапласа равен А4 Оптимальный проект по критерию Вальда (максимина) равен А2 Оптимальный проект по критерию Гурвица(показатель пессимизма a=½) равен А3 Оптимальный проект по критерию Сэдвижа,преобразовав матрицу выигрышей в матрицу рисков равен А1,А3, А4 Проект с минимальными затратами по критерию Лапласа равен А2 Проект с минимальными затратами по критерию Вальда (минимакса) равен А2 Проект с минимальными затратами по критерию Гурвица(показатель оптимизма a=1/3) равен А2 Оптимальным решением задачи нелинейного выпуклого программирования на минимум функции f называется такая точка Дана функция Метод нелинейного программирования, который рационально использовать при решении ЗНП с n переменными, если целевая функция нелинейная, а система ограничений содержит только уравнения – это Метод множителей Лагранжа Оптимальным решением задачи нелинейного выпуклого программирования на максимум функции f называется такая точка из множества допустимых значений, для которой справедливо неравенство Дана функция Дана функция Метод нелинейного программирования, который рационально использовать при решении ЗНП с двумя переменными, если целевая функция нелинейная, а система ограничений содержит только неравенства – это Графический метод Дана функция Для задачи максимизации вогнутой вниз функции на выпуклом множестве любая точка локального экстремума является и точкой Глобального минимума Градиентом функции n переменных называется Вектор, компоненты которого равны частным производным функции по соответствующим переменным Стоимость перевозок для плана, полученного методом Фогеля (вычеркивания) равна 630 Система уравнений для расчета потенциалов поставщиков и потребителей имеет вид U1 + V1 = 4, U2 + V1 = 6, U2 + V2 = 3, U3 + V2 = 4 Разности потенциалов, которые необходимо рассчитать при проверке данного плана на оптимальность ∆12, ∆31 Стоимость перевозок по данному плану равна 418 Матрица перевозок для данного плана равна 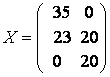 Если после получения оптимального решения мы внесем в нее сделанное ранее ограничение: x22 ≥ 5, то матрица перевозок примет вид 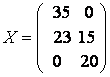 При проверке плана на невырожденность следует план вырожденный Разности потенциалов, которые необходимо рассчитать при проверке данного плана на оптимальность раны ∆11, ∆13, ∆23, ∆31, ∆33 Составить цикл для заполнения клетки (1, 2) можно, если поставить в какую-либо клетку таблицы вместо объема перевозок 0 Тогда баланс транспортной модели равен 470 Правильное ограничение для второй строки транспортной таблицы равно Баланс транспортной модели равен 37 Целевая функция данной задачи равна Правильное ограничение для первого столбца транспортной таблицы имеет вид Целевая функция задачи равна Стоимость перевозок для плана, полученного методом северо-западного угла равна 446 Стоимость перевозок для плана, полученного методом минимального элемента равна 146 Задача линейного программирования называется канонической (или основной), если система ограничений включает в себя только равенства Если в задаче линейного программирования допустимое множество не пусто и целевая функция ограничена, то существует хотя бы одно оптимальное решение Задача линейного программирования называется стандартной, если система ограничений включает в себя только неравенства Симплекс-метод предназначен для решения задачи линейного программирования, записанной в __________ виде каноническом Любой n-мерный вектор X=(x1,x2,…,xn)удовлетворяющий системе ограничений и условиям неотрицательности, называется допустимым решением Все линии уровня параллельны друг другу Если линии уровня перемещать в направлении их нормали, то они параллельны друг другу При нахождении минимума целевой функции графическим методом нужно перемещать линию уровня до опорной прямой в направлении, противоположном направлению нормали Неизвестные в допустимом виде системы ограничений ЗЛП, которые выражены через остальные неизвестные, называются базисными Система ограничений ЗЛП, записанной в канонической форме, имеет бесчисленное множество решений, если число неизвестных больше числа уравнений Полученноесимплекс-методом решение оптимально, если все элементы последней строки неотрицательны При составлении основной задачи линейного программирования ограничение-неравенство вида « » преобразуют в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной Линия уровня является опорной прямой, если имеет общую точку с многоугольником решений, перпендикулярна нормали, многоугольник решений находится в одной из полуплоскостей по отношению к ней Выбор переменной, выводимой из списка базисных, в симплекс-методе осуществляется нахождением минимального положительного отношения элементов столбца свободных членов к элементам разрешающего столбца Если в найденном методом искусственного базиса оптимальном плане расширенной задачи значения искусственных переменных равны нулю, то получен оптимальный план исходной задачи Матрица коэффициентов при неизвестных в системе ограничений двойственной задачи получают из аналогичной матрицы исходной задачи транспонированием Если -тое соотношение в системе ограничений двойственной задачи является уравнением, то переменная исходной задачи неопределенна В симметричной паре двойственных задач ограничениями являются равенства, переменные могут принимать только неотрицательные значения Если целевая функция одной из пары двойственных задач не ограничена, то другая задача не имеет решения  имеет вид имеет вид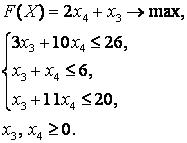 Основная форма задачи 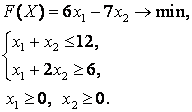 имеет вид имеет вид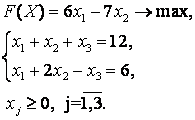 расширенной задачей является 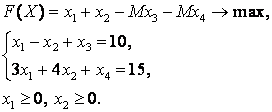 является X0=(0,0,–5,–2,–7) в первой итерации разрешающим элементом будет симплекс-методом будет X0=(1,0,3,2,0) |
