высшая математика. 2 13 Случайная величина распределена нормально с параметрами 3 и 2(N3,2). Ее математическое ожидание и дисперсия равны mx 3 dx 4
 Скачать 0.84 Mb. Скачать 0.84 Mb.
|
|
303. Разложить в ряд Тейлора функцию по степеням (х+2) 304. Разложить в ряд Фурье функцию 305. Разложить в ряд Тейлора функцию в окрестности х0=1 306. Разложить в ряд Фурье функцию 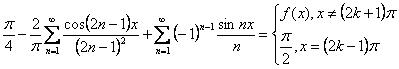 307. Разложить в ряд Фурье функцию ; ; 308. Разложить в ряд Фурье функцию ; ; ( - нецелое); 309. Разложить в ряд Фурье функцию ; ; 310. Разложить в ряд Тейлора функцию f(x)= по степеням х 311. Разложить в ряд Тейлора функцию f(x)= по степеням х+2 312. Разложить в ряд Тейлора функцию f(x)= степеням х 313. Определить интервал сходимости ряда 314. Найти область сходимости ряда 315. Найти область сходимости ряда 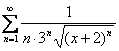 316. Найти область сходимости ряда 317. Найти область сходимости ряда 0;+ ) 318. Определить интервал сходимости ряда 319. Определить радиус сходимости ряда 320. Определить интервал сходимости ряда 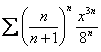 321. Определить радиус сходимости ряда 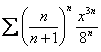 R= R= 322. Определить интервал сходимости ряда 323. Определить радиус сходимости ряда R= 324. Определить интервал сходимости ряда (-1/10;1/10) 325. Определить радиус сходимости ряда R=1/10 326. Определить интервал сходимости ряда (-6;0) 327. Определить радиус сходимости ряда R=3 238. Определить интервал сходимости ряда 239. Определить радиус сходимости ряда R=1/3 240. Определить интервал сходимости ряда расходится всюду 341. Определить интервал сходимости ряда ; 342. Определить интервал сходимости ряда 343. Определить радиус сходимости ряда R= 344. Определить интервал сходимости ряда ; 345. Определить интервал сходимости ряда 346. Определить интервал сходимости ряда 347. Определить интервал сходимости ряда (2-е; 2+е) 348. Пользуясь необходимым признаком сходимости ответить на вопрос о сходимости или расходимости ряда ряд расходится; 349. Исследовать на сходимость ряд сходится; 350. Исследовать на сходимость ряд ряд сходится 351. Пользуясь необходимым признаком сходимости ответить на вопрос о сходимости или расходимости ряда ряд расходится 352. Исследовать на сходимость ряд ряд расходится 353. Пользуясь необходимым признаком сходимости ответить на вопрос о сходимости или расходимости ряда ряд расходится 354. Исследовать на сходимость ряд ряд сходится 355. Пользуясь необходимым признаком сходимости ответить на вопрос о сходимости или расходимости ряда ряд расходится 356. Исследовать на сходимость ряд ряд сходится 357. Исследовать на сходимость ряд ряд сходится условно 358. Исследовать на сходимость ряд ряд сходится условно 359. Исследовать на сходимость ряд 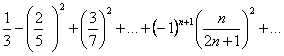 ряд расходится 360. Исследовать на сходимость ряд ряд сходится условно 361. Исследовать на сходимость ряд ряд сходится абсолютно 362. Исследовать на сходимость ряд ряд расходится 363. Исследовать на сходимость ряд ряд сходится абсолютно 364. Исследовать на сходимость ряд ряд сходится 365. 19. Исследовать на сходимость ряд ряд сходится 366. Исследовать на сходимость ряд ряд расходится 367. Исследовать на сходимость ряд ряд сходится 368. Исследовать на сходимость ряд ряд сходится 369. Исследовать на сходимость ряд ряд сходится 370. Исследовать на сходимость ряд ряд расходится 371. Исследовать на сходимость ряд ряд расходится вопрос о сходимости остается открытым 372. 393. Дан вариационный ряд выборки объема n = 8: -2, 0, 3, 4, 6, 9, 12, 16. Выборочное среднее для этого ряда равно 6 373. Формула D (-X) = D(X): верна 374. Дана выборка объема n: х1, х2 , …, хn . Если каждый элемент выборки увеличить в 5 раз, то выборочное среднее возрастет в 5 раз, а выборочная дисперсия S 2 увеличится в 25 раз 375. Автомашина пришла из Минска в Могилев со скоростью 40 км/ч и сразу же повернула обратно. Скорость ее на обратном пути была на 20 км больше. Средняя скорость автомобиля равна 48 км/ч 376. С помощью метода наименьших квадратов по этим точкам строится прямая регрессии. Эта прямая для прибыли в марте дает значение (Указание. Определить это значение без построения прямой регрессии) 1056 377. Всегда ли верна формула М (Х+Y)= M(X) + M(Y)? только для независимых случайных величин Х и Y 378. Плотность распределения f(x) можно найти по функции распределения F(x) по формуле 379. Для 2-х нормальных независимых величин с одинаковыми дисперсиями получены выборки объема nx = 42 и nу = 20 с такими характеристиками: = 64, Sх 2 = 16, = 59, Sy 2 = 25. При уровне значимости α = 0,05 проверяется гипотеза о равенстве генеральных средних μx = μ y (конкурирующая гипотеза μx μ y). Опытное значение статистики Т, применяемой для проверки гипотезы Н0, равно 4,17. Гипотеза Мx = М y не проходит 380. Случайная величина Х распределена равномерно на отрезке [0, 1]. Случайная величина Y = X + 2 будет иметь равномерное распределение на отрезке [2, 3] 381. Случайная величина распределена равномерно на отрезке [0, 5]. Р1 – вероятность, что случайно брошенная точка попадет на отрезок [0, 1]. Р2 – вероятность, что случайно брошенная точка попадет на отрезок [3, 4]. Тогда можно утверждать, что Р1=Р2 382. Для того чтобы изучить функциональную тенденцию изменения наблюдаемой величины во времени, следует построить график 383. В таблице статистического распределения, построенного по выборке, на одно число попала клякса х j 10 20 30 40 р j 0,1 0,2 х 0,5 Это число 0,2 384. Дано выборочное распределение хi 1250 1275 1280 1300 ni 20 25 50 5 Значение полигона, построенного по данному выборочному распределению, в точке 1280 и моды равны 50; 1280 385. Дана выборка значений 1, 5, 4, 2, 3 . Найти медиану. 3 386. Значение кумуляты, построенной по таблице, в точке 170, и медианы равны 0,8; 166 387. В таблице статистического распределения, построенного по выборке, одна цифра написана неразборчиво х j 1 2 3 4 n j 0,13 0,27 0,2х 0,35 5 388. Дан вариационный ряд выборки объема n = 8: -2, 0, 3, 4, 6, 9, 12, 16. Выборочная медиана d для этого ряда равна d = 5; 389. Вариационный ряд выборки: -7, 2, 4, 0, 3, 2, 1, -5 имеет вид -7, -5, 0, 1, 2, 2, 3, 4 390. Было проведено выборочное обследование доходов жителей. Оказалось, что половина жителей имеет доходы от 0 до 400 рублей, а половина – от 400 до 2000 рублей. По этим данным построили гистограмму. Она имеет вид 391. Вариационный ряд выборки: -7, 2, 4, 0, 3, 2, 1, -5 имеет вид -7, -5, 0, 1, 2, 2, 3, 4 392. Дано статистическое распределение выборки объема n = 50 Варианты х j 1 4 6 Относит. частоты р j 0,2 0,3 0,5 Эмпирическая функция распределения для этого ряда имеет вид 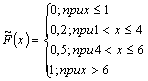 393. Дана конкретная выборка объема n = 10: 2, 2, 5, 5, 4, 3, 4, 2, 2, 5. Статистическое распределение этой выборки имеет вид Варианты х j 2 3 4 5 Частоты р j 0,4 0,1 0,2 0,3 394. Дан вариационный ряд выборки объема n = 10: -2, 0, 3, 3, 4, 5, 9, 11, 12, 15. Выборочная медиана для этого ряда – d равна 4,5 395. Дана выборка объема n= 7: 3, 5, -2, 1, 0, 4, 3. Вариационный ряд для этой выборки и размах вариационного ряда -2, 0, 1, 3, 3, 4, 5; размах равен 7 396. Дан вариационный ряд выборки объема n = 9: -2, 0, 3, 3, 4, 5, 9, 11, 12. Выборочная медиана для этого ряда – d равна 4 397. Дан вариационный ряд выборки объема n = 7: -5, -3, 0, 1, 1, 4, 16. Выборочная медиана d и выборочное среднее для этого ряда равны d = 1; = 2 398. Дана выборка объема n = 5: -4, -2, 2, 6, 8. Выборочная дисперсия равна 20,8 399. Самое маленькое значение в выборке 0, самое большое 8, медиана 2. По этой выборке построена гистограмма 400. По выборке 1, 0, 4, 3, 2 построен полигон 401. Дана выборка объема n= 7: 3, 5, -2, 1, 0, 4, 3. Вариационный ряд для этой выборки и размах вариационного-2, 0, 1, 3, 3, 4, 5; размах равен 7 402. Построить гистограмму и полигон распределения роста школьников по таблице  403. Дана выборка: 0, 5, 2, 8, 2, 6, 1, 5. Вариационный ряд для этой выборки и размах вариационного ряда 0, 1, 2, 2, 5, 5, 6, 8; размах выборки 8 404. Дан вариационный ряд выборки объема n = 7: -5, -3, 0, 1, 1, 4, 16. Выборочное среднее для этого ряда равно 2 405. Дано статистическое распределение выборки Варианты х j -3 1 3 11 Частоты р j 0,4 0,2 0,3 0,1 Выборочное среднее равно. 1 406. Медиана выборки х j -1 - 0 0 - 1 1 - 2 2 - 3 m j 30 70 80 20 1,5 407. Дана выборка объема n = 10: 0, 2, 3, 5, 5, 6, 6, 7, 8, 9. Выборочное среднее равно = 5,1 408. Процедура сопоставления высказанной гипотезы с выборочными данными называется Проверкой гипотезы 409. Если отвергается основная гипотеза, тогда как на самом деле она верна, то Допускается ошибка первого рода 410. Если принимается основная гипотеза, тогда как на самом деле она неверна, то Допускается ошибка второго рода 411. Если отвергается основная гипотеза, тогда как на самом деле верна альтернативная гипотеза, то Принято верное решение 412. Если принимается основная гипотеза, тогда как на самом деле неверна альтернативная гипотеза, то Принято верное решение 413. При проверке гипотезы о числовом значении математического ожидания нормального распределения при известной дисперсии надо пользоваться таблицами Нормального распределения 414. При проверке гипотезы о числовом значении математического ожидания нормального распределения при неизвестной дисперсии надо пользоваться таблицами Распределения Стьюдента 415. При проверке гипотезы о числовом значении дисперсии нормального распределения надо пользоваться таблицами Распределения Пирсона 416. При проверке гипотезы о равенстве математических ожиданий двух нормальных распределений с известными дисперсиями надо пользоваться таблицами Нормального распределения 417. При проверке гипотезы о равенстве математических ожиданий двух нормальных распределений с неизвестными, но равными дисперсиями надо пользоваться таблицами Распределения Стьюдента 418. При проверке гипотезы о равенстве дисперсий двух нормальных распределений надо пользоваться таблицами Распределения Фишера 419. При проверке гипотезы о числовом значении вероятности события надо пользоваться таблицами Нормального распределения 420. Критерии, с помощью которых проверяется гипотеза о модели закона распределения, называются Критерием сог ласия |
