Интервальные оценки параметров распределения - определение и вычисление с примерами решения. Интервальные оценки 3 Характеристики вариационного ряда 3
 Скачать 0.57 Mb.
|
1 2 Содержание Интервальные оценки 3 Характеристики вариационного ряда 3 Вариационные ряды 3 Построение интервального вариационного ряда 6 Графическое изображение вариационных рядов 7 Средние величины 9 Свойства эмпирической дисперсии 13 Эмпирические центральные и начальные моменты 15 Эмпирические асимметрия и эксцесс 18 Интервальные оценки параметров распределений 20 Доверительный интервал для математического ожидания случайной величины X при известной дисперсии 21 Доверительный интервал для математического ожидания нормальной случайной величины Х при неизвестной дисперсии 23 Доверительный интервал для дисперсии или нормальной случайной величины Х 26 Список использованной литературы 29 1 Интервальные оценки При статистической обработке результатов наблюдений необходимо знать не только точечную оценку  параметра но и уметь оценить точность этой оценки.Характеристики вариационного ряда Вариационные ряды Установление закономерностей, которым подчиняются массовые случайные явления, основано на изучении статистических данных ‒ сведений о том, какие значения принял в результате наблюдений интересующий исследователя признак. Пример. Исследователь, интересующийся тарифным разрядом рабочих механического цеха, в результате опроса 100 рабочих получил следующие сведения:  Здесь признаком является тарифный разряд, а полученные о нём сведения образуют статистические данные. Для изучения данных прежде всего необходимо их сгруппировать. Расположим наблюдавшиеся значения признака в порядке возрастания. Эта операция называется ранжированием статистических данных. В результате получим следующий ряд, который называется ранжированным: (1, 1, 1, 1) ‒ 4 раза; (2, 2, 2, 2, 2, 2) ‒ 6 раз; (3, 3, ..., 3) ‒ 12 раз; (4, 4, ..., 4) ‒ 16 раз; (5, 5, ..., 5) ‒ 44 раза; (6, 6, ..., 6) ‒ 18 раз. Из ранжированного ряда следует, что признак (тарифный разряд) принял шесть различных значений: первый, второй и т.д. до шестого разряда. В дальнейшем различные значения признака условимся называть вариантами, а под варьированием ‒ понимать изменение значений признака. Если признак по своей сущности таков, что различные его значения не могут отличаться друг от друга меньше, чем на некоторую конечную величину, то говорят, что это дискретно варьирующий признак. Тарифный разряд ‒ дискретно варьирующий признак: его различные значения не могут отличаться друг от друга меньше, чем на единицу. В примере этот признак принял 6 различных значений ‒ 6 вариантов: вариант 1 повторился 4 раза, вариант 2 ‒ 6 раз и т.д. Число показывающее, сколько раз встречается вариант л* в ряде наблюдений, называется частотой варианта 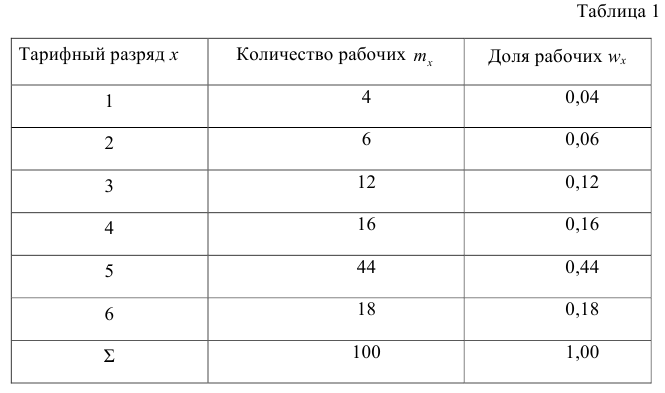 Ранжированный ряд представим в виде табл. 1. Вместо частоты варианта x можно рассматривать её отношение к общему числу наблюдений n, которое называется частостью варианта х и обозначается  Так как общее число наблюдений равно сумме частот всех вариантов  то справедлива следующая цепочка равенств:   Таблица, позволяющая судить о распределении частот (или частостей) между вариантами, называется дискретным вариационным рядом. В примере 1 была поставлена задача изучить результаты наблюдений. Если просмотр первичных данных не позволил составить представление о варьировании значений признака, то, рассматривая вариационный, ряд, можно сделать следующие выводы: тарифный разряд колеблется от 1‒го до 6‒го; наиболее часто встречается 5‒й тарифный разряд; с ростом тарифного разряда (до 5‒го разряда) растёт число рабочих, имеющих соответствующий разряд. Наряду с понятием частоты используют понятие накопленной частоты, которую обозначают 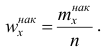 Накопленная частота показывает, во скольких наблюдениях признак принял значения, меньшие заданного значения х. Отношение накопленной частоты к общему числу наблюдений называют накопленной частостью и обозначают Очевидно, что  В дискретном вариационном ряду накопленные частоты вычисляются для каждого варианта и являются результатом последовательного суммирования частот (частостей). Накопленные частоты (частости) для вариационного ряда, заданного в табл. 1, вычислены в табл. 2. 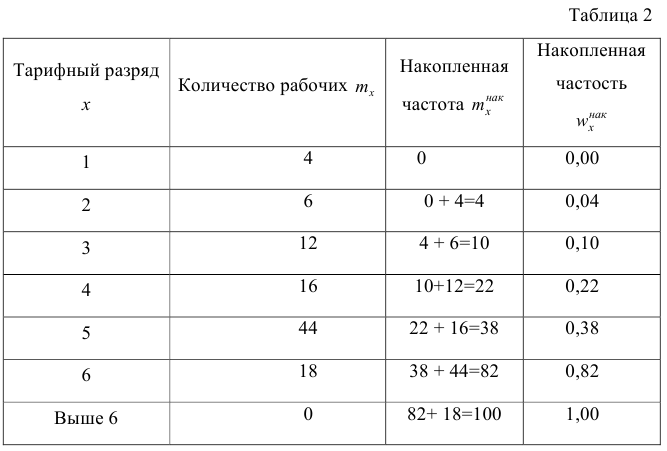 Например, варианту 1 соответствует накопленная частота, равная нулю, так как среди опрошенных рабочих не было таких, у которых тарифный разряд был бы меньше 1‒го; варианту 5 соответствует накопленная частота 38, так как было 4+6+12+16 рабочих с тарифным разрядом, меньшим 5‒го, накопленная частость для этого варианта равна 0,38 (38: 100); если тарифный разряд выше 6‒го, то ему соответствует накопленная частота 100, так как тарифный разряд всех опрошенных рабочих не выше 6‒го. 1.1.2 Построение интервального вариационного ряда Для построения интервального вариационного ряда необходимо определить величину интервала, установить полную шкалу интервалов, в соответствии с ней сгруппировать результаты наблюдений. В примере 2 при выборе величины интервала учитывались требования наибольшего удобства отсчётов. Интервал был принят равным 10% и оказался удачным. Построенный интервальный ряд позволил выявить закономерности варьирования значений признака. Для определения оптимального интервала h, т.е. такого, при котором построенный интервальный ряд не был бы слишком громоздким и в то же время позволял выявить характерные черты рассматриваемого явления, можно использовать формулу Стэрджеса:  где  ‒ соответственно максимальный и минимальный варианты.Если h ‒ дробное число, то за величину интервала следует взять либо ближайшее целое число, либо ближайшую несложную дробь. За начало первого интервала рекомендуется принимать величину 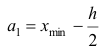 начало второго интервала совпадает с концом первого и равно начало третьего интервала совпадает с концом второго и равно  Построение интервалов продолжают до тех пор, пока начало следующего по порядку интервала не будет больше  После установления шкалы интервалов следует сгруппировать результаты наблюдений. Границы последовательных интервалов записывают в столбец слева, а затем, просматривая статистические данные в том порядке, в каком они были получены, проставляют чёрточки справа от соответствующего интервала. В интервал включается данные, большие или равные нижней границе интервала и меньшие верхней границы. Целесообразно каждые пятое и шестое наблюдения отмечать диагональными черточками, пересекающими квадрат из четырёх предшествующих. Общее количество чёрточек, проставленных против какого‒либо интервала, определяет его частоту. 1.1.3 Графическое изображение вариационных рядов Графическое изображение вариационного ряда позволяет представить в наглядной форме закономерности варьирования значений признака. Наиболее широко используются следующие виды графического изображения вариационных рядов: полигон, гистограмма, кумулятивная кривая. Полигон, как правило, служит для изображения дискретного вариационного ряда. Для его построения в прямоугольной системе координат наносят точки с координатами  где x ‒ вариант, а  ‒ соответствующая ему частота. Иногда вместо точек  строят точки (х;  . Затем эти точки соединяют последовательно отрезками. Крайние левую и правую точки соединяют соответственно с точками, изображающими ближайший снизу к наименьшему и ближайший сверху к наибольшему варианты. Полученная ломаная линия называется полигоном.Гистограмма служит для изображения только интервального вариационного ряда. Для её построения в прямоугольной системе координат по оси абсцисс откладывают отрезки, изображающие интервалы варьирования, и на этих отрезках, как на основании, строят прямоугольники с высотами, равными частотам (или частостям) соответствующего интервала. В результате получают ступенчатую фигуру, состоящую из прямоугольников, которую и называют гистограммой. Если по оси абсцисс выбрать такой масштаб, чтобы ширина интервала была равна единице, и считать, что по оси ординат единица масштаба соответствует одному наблюдению, то площадь гистограммы равна общему числу наблюдений, если по оси ординат откладывались частоты, и эта площадь равна единице, если откладывались частости. Иногда интервальный ряд изображают с помощью полигона. В этом случае интервалы заменяют их серединными значениями и к ним относят интервальные частоты. Для полученного дискретного ряда строят полигон. Кумулятивная кривая (кривая накопленных частот или накопленных частостей) строится следующим образом. Если вариационный ряд дискретный, то в прямоугольной системе координат строят точки с координатами  где х ‒ вариант,  ‒ соответствующая накопленная частота. Иногда вместо точек строят точки  Полученные точки соединяют отрезками.Если вариационный ряд интервальный, то по оси абсцисс откладывают интервалы. Верхним границам интервалов соответствуют накопленные частоты (или накопленные частости); нижней границе первого интервала ‒ накопленная частота, равная нулю. Построив кумулятивную кривую, можно приблизительно установить число наблюдений (или их долю в общем количестве наблюдений), в которых признак принял значения, меньшие заданного. Построение вариационного ряда ‒ первый шаг к осмысливанию ряда наблюдений. Однако на практике этого недостаточно, особенно когда необходимо сравнить два ряда или более. Сравнению подлежат только так называемые однотипные вариационные ряды, т.е. ряды, которые построены по результатам обработки сходных статистических данных. Например, можно сравнивать распределения рабочих по возрасту на двух заводах или распределения времени простоев станков одного вида. Однотипные вариационные ряды обычно имеют похожую форму при графическом изображении, однако могут отличаться друг от друга, а именно: иметь различные значения признака, вокруг которых концентрируются наблюдения (меры этой качественной особенности называется средними величинами); различаться рассеянием наблюдений вокруг средних величин (меры этой особенности получили название показателей вариации). Средние величины и показатели вариации позволяют судить о характерных особенностях вариационного ряда и называются статистическими характеристиками. К статистическим характеристикам относятся также показатели, характеризующие различия в скошенности полигонов и различия в их островершинности. 1.2 Средние величины Средние величины являются как бы «представителями» всего ряда наблюдений, поскольку вокруг них концентрируются наблюдавшиеся значения признака. Заметим, что только для качественно однородных наблюдений имеет смысл вычислять средние величины. Различают несколько видов средних величин: средняя арифметическая, средняя геометрическая, средняя гармоническая, средняя квадратическая, средняя кубическая и т.д. При выборе вида средней величины необходимо прежде всего ответить на вопрос: какое свойство ряда мы хотим представить средней величиной или, иначе говоря, какая цель преследуется при вычислении средней. Это свойство, получившее название определяющего, и определяет вид средней. Наиболее распространенной средней величиной является средняя арифметическая. Пусть  ‒ данные 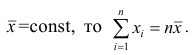наблюдений; ‒ средняя арифметическая. Свойство, определяющее среднюю арифметическую, формулируется следующим образом: сумма результатов наблюдений должна остаться неизменной, если каждое из них заменить средней арифметической: Так как  Отсюда получаем следующую формулу для вычисления средней арифметической по данным наблюдений: Если по наблюдениям построен вариационный ряд, то средняя арифметическая  где x ‒ вариант, если ряд дискретный, и центр интервала, если ряд интервальный;  ‒ соответствующая частота.Частоты в формуле (4) называют весами, а операцию умножения x на ‒ операцией взвешивания. Среднюю арифметическую, вычисленную по формуле (4), называют взвешенной в отличие от средней арифметической, вычисленной по формуле (3).Очевидно, что если по данным наблюдений построен дискретный вариационный ряд, то формулы (3) и (4) дают одинаковые значения средней арифметической. Если же по наблюдениям построен интервальный ряд, то средние арифметические, вычисленные по формулам (3) и (4), могут не совпадать, так как в формуле (4) значения признака внутри каждого интервала принимаются равными центрам интервалов. Ошибка, возникающая в результате такой замены, вообще говоря, очень мала, если наблюдения, распределены равномерно вдоль каждого интервала, а не скапливаются к одноименным границам интервалов. Среднюю арифметическую для вариационного ряда можно вычислять по формуле  которая является следствием формулы (4). Действительно, 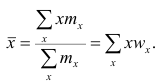 Свойство, определяющее среднюю арифметическую, сводилось к требованию неизменности суммы наблюдений при замене каждого из них средней арифметической. При решении практических задач может оказаться необходимым вычислить такую среднюю  при замене которой каждого наблюдения, осталась бы неизменной сумма степеней наблюдений, т.е. чтобы где q ‒ положительное или отрицательное число. Среднюю называют степенной средней q‒го порядка. Из определяющего свойства (6) получим следующую формулу для вычисления по данным наблюдений:  Сравнивая формулы (7) и (3), можно сделать вывод, что степенная средняя первого порядка есть не что иное, как средняя арифметическая, т.е.  При q=-l из формулы (7) получаем выражение для средней гармонической, при q=2 ‒ для среднеквадратической, при q=3 ‒ для средней кубической и т.д. Средней геометрической 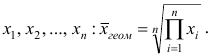 называют корень n‒й степени из произведения наблюдений  Можно доказать, что средняя геометрическая является предельным случаем степенной средней q‒го порядка при q=0, т.е.  Рассмотрим основные свойства средней арифметической. 1. Сумма отклонений результатов наблюдений от средней арифметической равна нулю. 2. Если все результаты наблюдений уменьшить (увеличить) на одно и то же число, то средняя арифметическая уменьшится (увеличится) на то же число. (Доказательство свойств 2 и 3 проведём в предположении, что по результатам наблюдений построен вариационный ряд и средняя арифметическая ‒ взвешенная). 3. Если все результаты наблюдений уменьшить (увеличить) в одно и то же число раз, то средняя арифметическая уменьшится (увеличится) во столько же раз. 4. Если ряд наблюдений состоит из двух групп наблюдений, то средняя арифметическая всего ряда равна взвешенной средней арифметической групповых средних, причём весами являются объёмы групп. Пусть 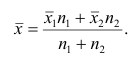 число наблюдений соответственно в 1‒й и 2‒й группах; ‒ средняя арифметическая для всего ряда  наблюдений; ‒ средние арифметические соответственно для 1‒й и 2‒й групп наблюдений. Требуется доказать, что: 5. Средняя арифметическая для сумм (разностей) взаимно соответствующих значений признака двух рядов наблюдений с одинаковым числом наблюдений равна сумме (разности) средних арифметических этих рядов. Пусть  ‒ один ряд наблюдений, ‒ его средняя арифметическая;  ‒ другой ряд наблюдений, ‒ его средняя арифметическая  ‒ ряд сумм соответствующих наблюдений,  ‒ его средняя арифметическая. Требуется доказать, что  Вычисление средней арифметической вариационного ряда непосредственно по формуле (4) приводит к громоздким расчётам, если числовые значения вариантов и соответствующие им частоты велики. Поэтому часто используют следующий способ, основанный на свойствах 3° и 2° средней арифметической: среднюю вычисляют не по первоначальным вариантам л‒, а по уменьшенным на не которое число с, а затем разделённым на некоторое число k т.е. для вариантов  Зная среднюю арифметическую для измененного ряда, легко вычислить среднюю арифметическую для первоначального ряда: Действительно, принимая во внимание свойства 3° и 2° средней арифметической, получаем  откуда следует, что Очевидно, что от выбора числовых значений с и к зависит, насколько простым будет вычисление средней арифметической для измененного ряда. Значения с и k обычно выбирают так, чтобы новые варианты  были небольшими целыми числами. Если ряд дискретный, то в качестве с берётся вариант, занимающий серединное положение в вариационном ряду (если таких вариантов два, то за k принимается тот, которому соответствует большая частота); за k принимают наибольший общий делитель вариантов (х‒с). Если ряд интервальный, то его заменяют дискретным; тогда с ‒ центр серединного интервала (если таких интервала два, то берётся тот, которому соответствует большая частота); за к принимают длину интервала h.1.2.1 Свойства эмпирической дисперсии Рассмотрим основные свойства эмпирической дисперсии, знание которых позволит упростить её вычисление. 1. Дисперсия постоянной величины равна нулю. Доказательство этого свойства очевидно вытекает из того, что дисперсия является показателем рассеяния наблюдений вокруг средней арифметической, а средняя арифметическая постоянной равна этой постоянной. 2. Если все результаты наблюдений уменьшить (увеличить) на одно и то же число с, то дисперсия не изменится. 3. Если все результаты наблюдений уменьшить (увеличить) в одно и то же число k раз, то дисперсия уменьшится (увеличится) в  раз.Это свойство позволяет эмпирическую дисперсию вычислять не по данным вариантам, а по уменьшенным (увеличенным) в одно и то же число k раз. Если дисперсию, вычисленную для измененного ряда, увеличить (уменьшить) в  раз, то получим дисперсию для первоначального вариационного ряда.4. Если ряд наблюдений состоит из двух групп наблюдений, то дисперсия всего ряда равна сумме средней арифметической групповых дисперсий и средней арифметической квадратов отклонений групповых средних от средней всего ряда, причем при вычислении средних арифметических весами являются объемы групп. Пусть 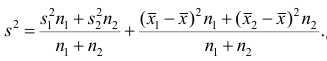 ‒ число наблюдений соответственно в 1‒й и 2‒й группах;  ‒ средние арифметические для 1‒й и 2‒й групп наблюдений; ‒ дисперсии для 1‒й и 2‒й групп наблюдений;  ‒ средняя арифметическая и дисперсия для всего ряда  наблюдений. Требуется доказать, что Свойство 4° можно обобщить на случай, когда ряд наблюдений состоит из любого количества  групп наблюдений. Введём понятия межгрупповой и внутригрупповой дисперсий.Если ряд наблюдений состоит из k групп наблюдений, то межгрупповой дисперсией 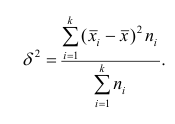 называют среднюю арифметическую квадратов отклонений групповых средних от средней всего ряда наблюдений причём весами являются объёмы групп т.е. Средней групповых дисперсий или внутригрупповой дисперсией 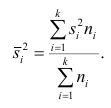 называют среднюю арифметическую групповых дисперсий причём весами являются объёмы групп  Следствие (свойства 4°). Если ряд наблюдений состоит из k групп наблюдений, то дисперсия всего ряда s2 равна сумме внутригрупповой и межгрупповой дисперсий, т.е.  Вычисление дисперсии вариационного ряда непосредственно по формуле (16) приводит к громоздким расчётам, если числовые значения вариантов и соответствующие им частоты велики. Поэтому часто дисперсию вычисляют не по первоначальным вариантам х, а по вариантам  Зная  (дисперсию для измененного ряда), легко вычислить дисперсию для первоначального ряда: Действительно, принимая во внимание свойства 3° и 2° дисперсии, получаем 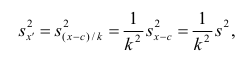 откуда следует, что  Требования к с и k предъявляют те же, что и в упрощенном способе вычисления средней арифметической. 1.2.2 Эмпирические центральные и начальные моменты Средняя арифметическая и дисперсия вариационного ряда являются частными случаями более общего понятия о моментах вариационного ряда. Эмпирическим начальным моментом  порядка q называют взвешенную среднюю арифметическую q‒x степеней вариантов, т.е. Эмпирический начальный момент нулевого порядка: 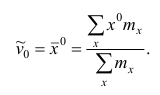 Эмпирический начальный момент первого порядка  Эмпирический начальный момент второго порядка и т.д. Эмпирическим центральным моментом  порядка q называют взвешенную среднюю арифметическую q‒x степеней отклонений вариантов от их средней арифметической, т.е. Эмпирический центральный момент нулевого порядка: 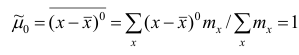 Эмпирический центральный момент первого порядка: 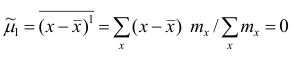 (в силу свойства 1° средней арифметической). Эмпирический центральный момент второго порядка: 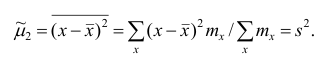 В дальнейшем для краткости величину  часто будем называть просто центральным моментом (начальным моментом), не употребляя термин «эмлирический».Используя формулу бинома Ньютона, разложим в ряд выражение для центрального момента q‒го порядка: 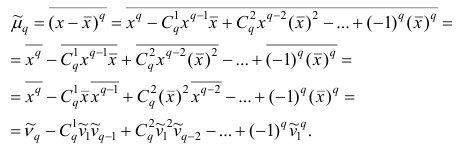 В проведенных тождественных преобразованиях использованы свойства 5° и 3° средней арифметической; 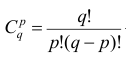 ‒ число сочетаний из q элементов по р элементов  Итак, центральный момент q‒го порядка выражается через начальные моменты следующим образом:  Полагая q = 0, 1, 2,..., можно получить выражения центральных моментов различных порядков через начальные моменты: 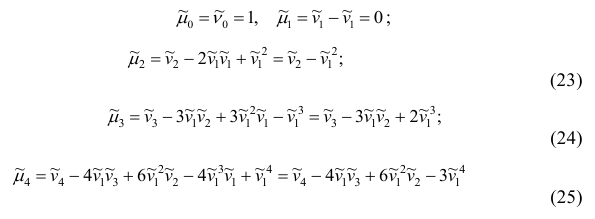 Заметим, что формула (23) для центрального момента второго порядка, как и следовало ожидать, аналогична формуле (18) для дисперсии. Рассмотрим свойства центральных моментов, которые позволят значительно упростить их вычисление. 1. Если все варианты уменьшить (увеличить) на одно и то же число с, то центральный момент q‒го порядка не изменится. 2. Если все варианты уменьшить (увеличить) в одно и то же число k раз, то центральный момент q‒го порядка уменьшится (увеличится) в  раз. Доказательство. Если все варианты уменьшить в одно и то же число k раз, то средняя арифметическая для измененного вариационного ряда равна 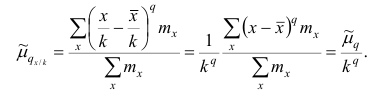 поэтому центральный момент q‒го порядка Аналогично можно показать, что  Для облегчения расчётов центральные моменты вычисляют не по первоначальным вариантам х, а по вариантам  Зная (центральный момент q‒го порядка для измененного ряда), легко вычислить центральный момент q‒го порядка для первоначального ряда: внимание свойства центрального момента, получаем 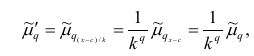 откуда следует, что  1.2.3 Эмпирические асимметрия и эксцесс Эмпирическим коэффициентом асимметрии называют отношение центрального момента третьего порядка к кубу среднеквадратического отклонения: 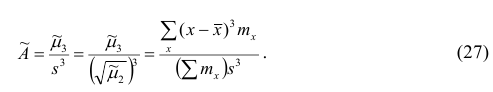 Если полигон вариационного ряда скошен, т.е. одна из его ветвей, начиная от вершины, зримо длиннее другой, то такой ряд называют асимметричным. Из формулы (27) следует, что если в вариационном ряду преобладают варианты, меньшие то эмпирический коэффициент асимметрии отрицателен; говорят, что в этом случае имеет место левосторонняя асимметрия. Если же в вариационном ряду преобладают варианты, большие то эмпирический коэффициент асимметрии положителен; в этом случае имеет место правосторонняя асимметрия. При левосторонней асимметрии левая ветвь полигона длиннее правой. При правосторонней, более длинной является правая ветвь. Эмпирическим эксцессом или коэффициентом крутости называют уменьшенное на 3 единицы отношение центрального момента четвертого порядка к четвертой степени среднеквадратического отклонения:  За стандартное значение эксцесса принимают нуль‒эксцесс так называемой нормальной кривой (см. рис. 1).  Кривые, у которых эксцесс отрицательный, по сравнению с нормальной менее крутые, имеют, более плоскую вершину и называются «плосковершинными» Кривые с положительным эксцессом более крутые по сравнению с нормальной кривой, имеют более острую вершину и называются «островершинными». 1 2 |