Интервальные оценки параметров распределения - определение и вычисление с примерами решения. Интервальные оценки 3 Характеристики вариационного ряда 3
 Скачать 0.57 Mb.
|
1 2 2 Интервальные оценки параметров распределений Доверительный интервал, доверительная вероятность: Точечная оценка неизвестного параметра , найденная по выборке объема из генеральной совокупности, не позволяет непосредственно узнать ошибку, которая получается, когда вместо точного значения неизвестного параметра принимается некоторое его приближение (оценка)  Поэтому чаще пользуются интервальной оценкой, основанной на определении некоторого интервала, накрывающего неизвестное значение параметра с определенной вероятностью. На рис. 10.1 изображен интервал длиной , внутри которого в любом месте может находиться неизвестное значение параметра . 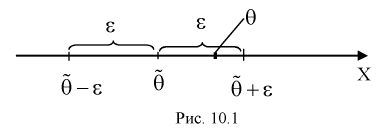 Чем меньше разность  тем лучше качество оценки. И если записать  то будет характеризовать точность оценки.Доверительной вероятностьюоценки называется вероятность  выполнения неравенства  . Доверительную вероятность р обычно задают заранее: 0,9; 0,95; 0,9973. И доверительная вероятность показывает, что с вероятностью р параметр будет накрываться данным интервалом  или (10.1)Из (10.1) видно, что неизвестный параметр находится внутри интервала  .Доверительным интерваломназывается интервал  накрывающий неизвестный параметр 0 с заданной доверительной вероятностью  Длина его (см. рис. 10.1) . Параметр ‒ уровень значимости. 2.1 Доверительный интервал для математического ожидания случайной величины X при известной дисперсии Пусть эксперимент Е описывается нормальной случайной величиной X. Плотность распределения 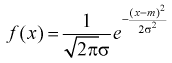 . Предположим, что известна дисперсия  ‒ неизвестна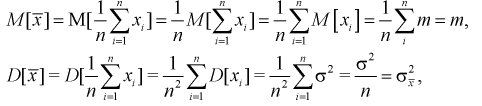. Тогда точечную оценку математического ожидания можно получить из выборки объемом ‒ и она определится так: Рассматривая выборку как независимых случайных величин, имеющих одно и тоже нормальное распределение, определим числовые характеристики  откуда получим 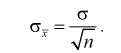 (10.2)Для определения доверительного интервала рассмотрим разность между оценкой и параметром: Нормируем ее (сделаем безразмерной), т.е. разделим на 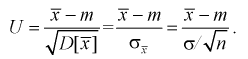 и обозначим как случайную величину U: (10.3)Покажем, что случайная величина U имеет нормированный нормальный закон распределения. Найдем ее числовые характеристики: 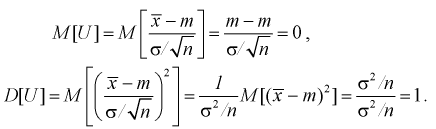 Таким образом  ‒ это значи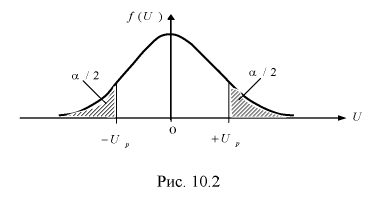т, что U имеет нормированное нормальное распределение, график которого изображен на рис. 10.2.  Зная плотность распределения случайной величины U, легко найти вероятность попадания случайной величины U в интервал  (см. рис. 1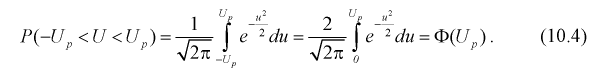0.2):  Левая часть этого уравнения представляет собой доверительную вероятность  Тогда из (10.4) и (10.5) следует уравнение  Решая уравнение (10.6), по таблицам функции Лапласа для заданной доверительной вероятности 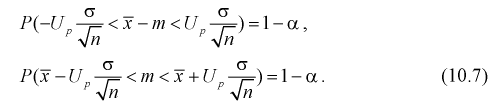 можно найти границы доверительного интервала для U, т. е. квантили . Считая, что квантили известны, преобразуем правую часть уравнения (10.5), подставляя в нее (10.3): Считая, что ‒ известна, из (10.7) следует, что доверительный интервал  накрывает неизвестное математическое ожидание с заданной доверительной вероятностью  Точность оценки математического ожидания или длина доверительного интервала  Замечания по формуле (10.8): при увеличении объема выборки из (10.8) видим, что е уменьшается, значит, уменьшается длина доверительного интервала, а точность оценки увеличивается; увеличение доверительной вероятности  приводит к увеличению длины доверительного интервала (см. рис. 10.2, где квантили увеличиваются), т. е. е увеличивается, а точность оценки падает;если задать точность е и доверительную вероятность , то можно найти объем выборки, который обеспечит заданную точность:  2.2 Доверительный интервал для математического ожидания нормальной случайной величины X при неизвестной дисперсии Пусть эксперимент описывается случайной величиной X с нормальным распределением с неизвестными параметрами Для определения точечных оценок этих параметров из генеральной совокупности извлечена выборка объемом . Тогда точечные оценки этих параметров определяются так: 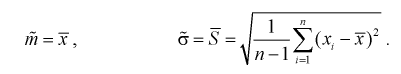 Здесь использовали для оценки дисперсии ‒ модифицированную выборочную дисперсию, несмещенную оценку. Для построения доверительного интервала рассмотрим разность между оценкой и параметром: . Нормируем ее, т. е. разделим на  и обозначим результат как случайную величину t. Ранее мы показали, что  но т.к. здесь неизвестна, возьмем ее оценку и тогда  . Тогда случайная величина t принимает вид Умножим числитель и знаменатель в (10.10) на 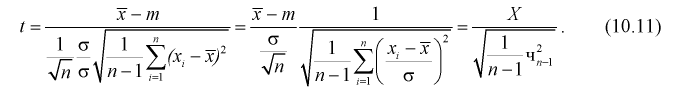 Здесь X ‒ нормированная нормальная случайная величина, знаменатель ‒ распределение с степенями свободы. Поэтому, согласно определению (см. раздел 9.3, формула (9.5)), можно утверждать, что случайные величины определяемые по формулам (10.10) и (10.11), имеют закон распределения Стьюдента с степенями свободы. Зная закон распределения случайной величины t и задавая доверительную вероятность 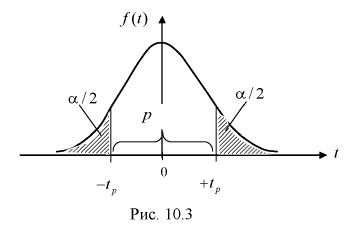 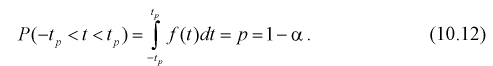, можно найти вероятность попадания ее в интервал (рис. 10.3).  Из таблиц распределений Стьюдента по заданной доверительной вероятности  и числу степеней свободы находим квантили удовлетворяющие условию Подставляя в (10.13) вместо t равенство (10.10), получаем 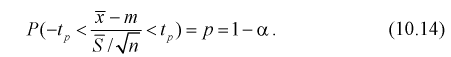 Разрешим неравенство в левой части формулы (10.14) относительно 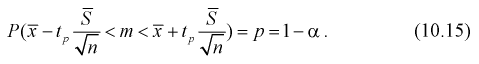 Отсюда непосредственно следует, что доверительный интервал 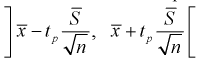 накрывает неизвестный параметр ‒ (математическое ожидание) с доверительной вероятностью Интервал (10.15) несколько шире интервала (10.7), определенного для той же выборки и той же доверительной вероятности. Зато в (10.15) используется меньшая априорная информация ‒ знать не надо. Можно обозначить ширину доверительного интервала или точность через , и из (10.15) следует  Все замечания, сделанные по формуле (10.8), справедливы и для формулы (10.16). 2.3 Доверительный интервал для дисперсии или ст нормальной случайной величины X Рассмотрим вероятностный эксперимент с нормальной моделью, где параметры неизвестны. Предположим, что по выборке найдены точечные оценки этих параметров: 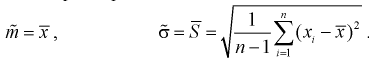 Составим вспомогательную случайную величину  Эта случайная величина имеет распределение 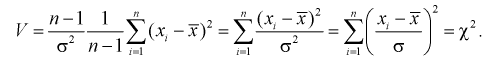 степенями свободы. Покажем это, подставив в (10.17) выражение для  Это и есть распределение хи‒квадрат с степенью свободы. На рис. 10.4 приведен график этого распределения. 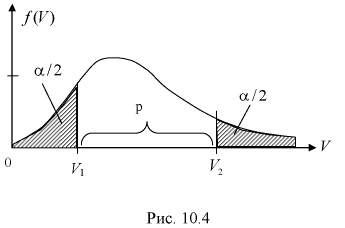 Зная закон распределения случайной величины У, определим вероятность того, что случайная величина попадет в интервал 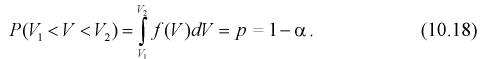  Здесь плотность распределения с степенями свободы. Из рис. 10.4 видно, что кривая для плотности распределения несимметрична относительно центра распределения, поэтому границы доверительного интервала или квантили 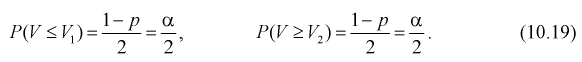 для данной вероятности не определяются однозначно. Чтобы избежать неопределенности будем их находить из условия Это означает, что площади заштрихованных фигур равны. Задавая доверительную вероятность  по таблицам распределения для числа степеней свободы используя условия (10.19), находим квантили  Считая и р известными, перепишем (10.18) в следующем виде:  Подставим в (10.20) значение , определяемое формулой (10.17):  Решаем неравенство в левой части (10.21) относительно 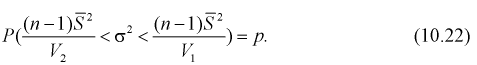 Из (10.22) записываем доверительный интервал для 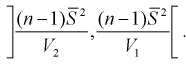 Для среднего квадратического отклонения доверительный интервал имеет следующий вид: 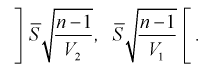 Можно ввести коэффициенты 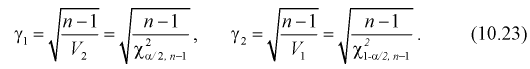 Тогда доверительный интервал для о определится следующим образом:  Коэффициенты  , соответствующие доверительной вероятности и числу степеней свободы , находятся по таблицам распределения . Список использованной литературы Боровков А.А. Математическая статистика. – М.: Наука, 2014. – 472 с. Гихман И.И., Скороход А.В., Ядренко М.И. Теория вероятностей и математическая статистика. – Киев: Вища школа, 2019. – 408 с. Ивченко Г.И., Медведев Ю.И. Математическая статистика: Учеб. пособие для втузов. – М.: Высшая школа, 2020. – 248 с. Климов Г.П. Теория вероятностей и математическая статистика. – М.: Изд-во Моск. ун-та, 2018. – 328 с. Математическая статистика: Учеб. для вузов/ В.Б. Горяинов, И.В. Павлов, Г.М. Цветкова и др. Под ред. В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2001 – 424 с. 1 2 |