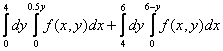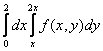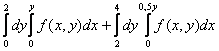Математическое ожидание и дисперсия случайной величины, распределенной равномерно на отрезке [1; 3], равны 2; 1/3
Случайная величина распределена «нормально с параметрами 3 и 2»(N[3,2]). Ее математическое ожидание и дисперсия равны MX = 3; DX = 4
Случайная величина распределена равномерно на отрезке [0, 4]. Вероятность попасть в интервал [1, 3] равна 0,5
Математическое ожидание и дисперсия случайной величины, имеющей плотность распределения , равны 2; 5
Известно, что X N (0, 3), Y
N (0,5, 2), X и Y независимы. S = X+2Y имеет распределение N (1, 7)
Плотность распределения f(x) можно найти по функции распределения F(x) по формуле
Математическое ожидание и дисперсия случайной величины, имеющей плотность распределения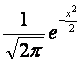 , равны 0; 1 , равны 0; 1
Случайная величина Х распределена равномерно на отрезке [0, 1]. Случайная величина Y = X + 2 будет иметь равномерное распределение на отрезке [2, 3]
Случайная величина распределена равномерно на отрезке [0, 5]. Р1 – вероятность, что случайно брошенная точка попадет на отрезок [0, 1]. Р2 – вероятность, что случайно брошенная точка попадет на отрезок [3, 4]. Тогда можно утверждать, что Р1=Р2
Математическое ожидание и дисперсия случайной величины, распределенной равномерно на отрезке [2, 6], равны 4; 4/3
Функцию распределения F(x) можно найти по плотности распределения f(x) по формуле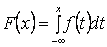
Для плотности распределения f(x) имеет место равенство
Для непрерывной случайной величины вероятность попасть в интервал равна
Случайная величина Х распределена «нормально с параметрами 3 и 2» - (N[3, 2]). Тогда плотность распределения равна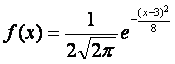
0,25
Страхуется 1600 автомобилей; вероятность того, что автомобиль может попасть в аварию, равна 0.2. По какой формуле можно вычислить вероятность того, что число аварий не превысит 350 интегральной формулой Муавра-Лапласа
События называются независимыми если р(АВ)=р(А)р(В)
Чему равна вероятность невозможного события 0
События А и В называются несовместными, если р(АВ)= 0
5. Вероятность выиграть в рулетку равна 1/38. Игрок делает 190 ставок. По какой формуле можно вычислить вероятность того, что он выиграет не менее 5 раз распределения Пуассона
Вероятность суммы любых случайных событий А и В вычисляется по формуле р(А+В)=р(А)+р((В)-р(АВ)
Вероятность выиграть в кости равна 1/6. Игрок делает 120 ставок. По какой формуле можно вычислить вероятность того, что число выигрышей не будет меньше 15 интегральной формулой Муавра-Лапласа
Производится n независимых испытаний, в которых вероятность наступления события А равна р. Вероятность того, что событие А наступит m раз вычисляется по формуле Бернулли
Если имеется группа из n несовместных событий Нi, в сумме составляющих все пространство, и известны вероятности Р(Нi), а событие А может наступить после реализации одного из Нi и известны вероятности Р(А/Нi), то Р(А) вычисляется по формуле полной вероятности
Если вероятность события А есть р(А), то чему равна вероятность события, ему противоположного 1-р(А)
Вероятность появления события А в испытании равна р. Чему равна дисперсия числа появления события А в одном испытании р(1-р)
Вероятность любого события всегда удовлетворяет следующему условию она не меньше 0 и не больше 1
Условной вероятностью события В при условии, что событие А с ненулевой вероятностью произошло, называется р(В/А)=р(АВ)/р(А)
Имеется группа из n несовместных событий Hi, в сумме составляющих все пространство, и известны вероятности P(Hi), а событне А может наступить после реализации одного из Hi, и заданы вероятности P(A/Нi). Известно, событие А произошло. Вероятность, что при этом была реализована Hi вычисляется по формуле Байеса
Чему равна вероятность достоверного события 1
Вероятность того, что дом может сгореть в течение года, равна 0.01. Застраховано 500 домов. По какой формуле можно вычислить вероятность того, что угорит не более 5 домов распределением Пуассона
В почтовом отделении продаются открытки пяти видов в неограниченном количестве. Сколькими способами можно купить 6 открыток 210
Сколькими способами можно расставить на полке 6 различных книг 720
Сколькими способами три награды могут быть распределены между 10 участниками соревнования 720
Сколько пар можно выбрать из 8 школьников 28
Имеется 10 учебных предметов и 5 разных уроков в день. Сколькими способами можно распределить уроки в день 252
Из состава конференции в 11 человека нужно избрать делегацию из 3 человек. Сколькими способами это можно сделать 165
Сколькими способами можно выбрать три дежурных из группы в 12 человека 220
Сколько четырехзначных чисел можно составить, имея цифры 3456 24
Сколько четырехзначных чисел можно составить, имея цифры 3446 12
Число грузовых машин, проезжающих мимо бензоколонки, относится к числу легковых машин, как 3:2. Известно, что в среднем одна из 30 грузовых и одна из 25 легковых машин останавливается для заправки. Вероятность того, что проезжающая машина будет заправляться равна. Ответ округлите до тысячных. 0,036
Число грузовых машин, проезжающих мимо бензоколонки, относится к числу легковых машин, как 3:2. Известно, что в среднем одна из 30 грузовых и одна из 25 легковых машин останавливается для заправки. Вероятность того, что заправившаяся машина будет легковой. Ответ округлите до тысячных. 0,444
Число грузовых машин, проезжающих мимо бензоколонки, относится к числу легковых машин, как 3:2. Известно, что в среднем одна из 30 грузовых и одна из 25 легковых машин останавливается для заправки. Вероятность того,что заправившаяся машина будет грузовой. Ответ округлите до тысячных. 0,556
С первого станка на сборку поступает 40% деталей, остальные 60% со второго. Вероятность изготовления бракованной детали для первого и второго станка соответственно равна 0.01 и 0.04. Вероятность того, что наудачу поступившая на сборку деталь окажется бракованной равна. Ответ округлите до тысячных. 0.028
В пирамиде 5 винтовок, 3 из которых снабжены оптическим прицелом. Вероятность попадания для стрелка при выстреле из винтовки с оптическим прицелом равна 0.95, из обычной винтовки - 0.7. Стрелок наудачу берет винтовку и стреляет. Вероятность того, что мишень будет поражена равна. 0.85
На некоторой фабрике машина А производит 40% продукции, а машина В - 60%. В среднем 9 из 1000 единиц продукции, произведенных машиной А, и 1 из.250, произведенных машиной В, оказываются бракованными. Вероятность, что случайно выбранная единица продукции окажется бракованной равна. Ответ округлите до тысячных.0,006
В цехе работают 20 станков. Из них 10 марки А, 6 марки В и 4 марки С. Вероятность того, что качество детали окажется отличным для этих станков соответственно равна 0,9; 0,8; 0,7. Вероятность отличных деталей выпускает цех в целом равна 0,83
В цехе работают 20 станков. Из них 10 марки А, 6 марки В и 4 марки С. Вероятность того, что качество детали окажется отличным для этих станков соответственно равна 0,9; 0,8; 0,7. Вероятность, что качественная деталь будет станка марка А равна. Ответ округлите до тысячных. 0,542
В цехе работают 20 станков. Из них 10 марки А, 6 марки В и 4 марки С. Вероятность того, что качество детали окажется отличным для этих станков соответственно равна 0,9; 0,8; 0,7. Вероятность, что качественная деталь будет станка марка В равна. Ответ округлите до тысячных. 0,289
В цехе работают 20 станков. Из них 10 марки А, 6 марки В и 4 марки С. Вероятность того, что качество детали окажется отличным для этих станков соответственно равна 0,9; 0,8; 0,7. Вероятность, что качественная деталь будет станка марка С равна. Ответ округлите до тысячных. 0,169
На склад поступает продукция трех фабрик, причем продукция первой фабрики составляет 20%, второй - 46%, третьей - 34%. Известно, что средний процент нестандартных изделий для первой фабрики равен 3%, для второй - 2%, для третьей - 1%. Вероятность того, что наудачу взятое изделие оказалось нестандартным равна. 0,0186
На склад поступает продукция трех фабрик, причем продукция первой фабрики составляет 20%, второй - 46%, третьей - 34%. Известно, что средний процент нестандартных изделий для первой фабрики равен 3%, для второй - 2%, для третьей - 1%. Вероятность того, что наудачу взятое изделие произведено на первой фабрики, если оно оказалось нестандартным равна. Ответ округлите до тысячных. 0,322
На склад поступает продукция трех фабрик, причем продукция первой фабрики составляет 20%, второй - 46%, третьей - 34%. Известно, что средний процент нестандартных изделий для первой фабрики равен 3%, для второй - 2%, для третьей - 1%. Вероятность того, что наудачу взятое изделие произведено на второй фабрики, если оно оказалось нестандартным равна. Ответ округлите до тысячных.0,495
На склад поступает продукция трех фабрик, причем продукция первой фабрики составляет 20%, второй - 46%, третьей - 34%. Известно, что средний процент нестандартных изделий для первой фабрики равен 3%, для второй - 2%, для третьей - 1%. Вероятность того, что наудачу взятое изделие произведено на третей фабрики, если оно оказалось нестандартным равно. Ответ округлите до тысячных.0,183
Предположим, что 5% всех мужчин и 2,5% всех женщин дальтоники. Вероятность, что наугад выбранное лицо страдает дальтонизмом равна. (считать, что мужчин и женщин одинаковое число). Ответ округлите до тысячных. 0,0375
Предположим, что 5% всех мужчин и 2,5% всех женщин дальтоники. Наугад выбранное лицо страдает дальтонизмом. Вероятность того, что это мужчина равна. (считать, что мужчин и женщин одинаковое число). Ответ округлите до тысячных. 0,666
Предположим, что 5% всех мужчин и 2,5% всех женщин дальтоники. Наугад выбранное лицо страдает дальтонизмом. Вероятность того, что это женщина равна. (считать, что мужчин и женщин одинаковое число). Ответ округлите до тысячных. 0,333
В мешке имеются 5 красных и 4 белых шара. Последовательно извлекается 3 шара. Вероятность того, что все они будут белыми. Ответ округлите до тысячных. 0,048
В мешке имеются 5 красных и 4 белых шара. Последовательно извлекается 3 шара. Вероятность того, что все они будут красными равна. Ответ округлите до тысячных. 0,119
В урне имеется 3 белых и 5 черных шаров. Из урны наугад выбираются 2 шара. Вероятность того, что среди этих шаров 1 белый и 1 черный равна. Ответ округлите до тысячных. 0,536
Из колоды карт в 36 карт одновременно извлекают две карты. Вероятность того, что одна карта дама, другая валет равна. Ответ округлите до тысячных. 0,025
Из колоды карт в 36 карт одновременно извлекают две карты. Вероятность того, что обе карты дамы равна. Ответ округлите до тысячных. 0,010
Из колоды карт в 36 карт одновременно извлекают две карты. Вероятность того, что обе карты валет равна. Ответ округлите до тысячных. 0,010
Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Вероятность того, что при аварии сработает только один сигнализатор равна 0,14
Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Вероятность того, что при аварии сработают оба сигнализатора равна 0,885
Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Вероятность того, что при аварии не сработает ни один сигнализатор равна 0,005
Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Вероятность того, что при аварии сработает хотя бы один сигнализатор равна 0,995
Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания для первого стрелка равна 0,75; для второго – 0,8; для третьего – 0,9. Вероятность того, что все три стрелка одновременно попадут в цель равна 0,54
Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания для первого стрелка равна 0,75; для второго – 0,8; для третьего – 0,9. Вероятность того, что никто из стрелков не попадет в цель равна 0,005
Рабочий обслуживает три станка. Вероятность того, что в течение часа станок потребует внимания рабочего, равна для первого станка 0.1, для второго - 0.2 и для третьего - 0.15. Вероятность того, что в течение некоторого часа хотя бы один из станков потребует внимания рабочего равна 0,388
Два стрелка стреляют по мишени. Вероятность попадания в цель у одного стрелка 0.6, у другого - 0.7. Вероятность того, что цель будет поражена двумя пулями равна 0,42
Станок производит изделия трех сортов. Первого сорта - 80%, второго - 15%. Вероятность того, что наудачу взятое изделие будет или второго, или третьего сорта равна 0,2
В группе 25 студентов, из которых отлично учится 5 человек, хорошо - 12, удовлетворительно - 6 и слабо - 2. Преподаватель вызывает студента. Вероятность того, что вызванный студент или отличник или хорошист равна 0,68
Три стрелка производят по одному выстрелу. Вероятности попадания 1-го, 2-го и 3-го стрелков соответственно равны: 0,2; 0,3 и 0,4. Вероятность получения одного попадания равна 0,452
Завод в среднем дает 27% продукции высшего сорта и 70% - первого сорта. Вероятность того, что наудачу взятое изделие не будет высшего или первого сорта равна 0,03
Лампочки изготавливаются независимо друг от друга. В среднем одна лампочка из тысячи оказывается бракованной. Вероятность того, что из двух взятых наугад лампочек окажутся исправными обе равна. Ответ округлите до тысячных 0,998
Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента при включении прибора - 0.05, второго - 0.08. Вероятность того, что при включении прибора оба элемента будут работать равна 0,874
Изделия изготавливаются независимо друг от друга. В среднем одно изделие из ста оказывается бракованным. Вероятность того, что в двух взятых наугад изделий окажутся неисправными оба равна 0,0001
Два стрелка стреляют по мишени. Вероятность попадания в цель у одного стрелка 0.7, у другого - 0.8. Найти вероятность того, что цель будет поражена. 0,94
В среднем каждое сотое изделие, производимое предприятием, дефектное. Взяли два изделия. Вероятность, что оба окажутся исправными равна 0,98
Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента при включении выбора –0,03, второго –0,06. Вероятность того, что при включении прибора откажет только второй элемент равна 0,0582
Экзаменационный билет содержит 3 вопроса. Вероятности того, что студент ответит на 1 и 2 вопросы равна 0,9 на 3 вопрос 0,8. Вероятность того, что студент сдаст экзамен, если для этого необходимо ответить хотя бы на 2 вопроса. 0.954
Электрическая схема имеет вид. Вероятность выхода из строя блоков p1=0.1; p2=0.2; p3=0.3. Вероятность работы цепи равна. 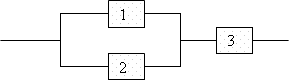 0,686 0,686
Произведен залп из двух орудий по мишени. Вероятность попадания из первого орудия равна 0.85 , из второго - 0.91. Вероятность поражения цели равна 0,9865
В электрическую цепь последовательно включены три элемента, работающие независимо один от другого. Вероятность отказов первого, второго и третьего элементов соответственно равны: p1=0.1, p2=0.15, p3=0.2. Вероятность того, что ток в цепи будет равна0,612
В магазин трикотажных изделий поступили носки, 60% которых получено от одной фабрики, 25% - от другой и 15% - от третьей. Вероятность того, что купленные покупателем носки изготовлены на второй или третьей фабрике равна 0,4
В электрическую цепь последовательно включены три элемента, работающие независимо один от другого. Вероятность отказов первого, второго и третьего элементов соответственно равны: p1=0.1, p2=0.15, p3=0.2. Вероятность того, что тока в цепи не будет. 0,388
Вратарь парирует в среднем 0.3 всех одиннадцатиметровых штрафных ударов. Вероятность того, что он возьмет ровно два из четырех мячей равна. Ответ округлите до тысячных. 0.265
Стрелок попадает в цель в среднем в 8 случаях из 10. Вероятность, что, сделав три выстрела, он два раза попадет равна. Ответ округлите до тысячных.0,384
Бросается 5 монет. Вероятность того, что три раза выпадет герб равна 0,3125
Вероятность попадания в мишень при 1 выстреле равна 0,9. Вероятность того, что при 6 выстрелах, попаданий будет ровно 4 равна.Ответ округлите до тысячных 0,098
Вероятность изготовления детали высшего сорта на данном станке равна 0,5. Найти наивероятнейшее число деталей высшего сорта среди 24 деталей. 12
Вероятность изготовления детали высшего сорта на данном станке равна 0,7. Найти наивероятнейшее число деталей высшего сорта среди 24 деталей 17
Вероятность, что событие появится три раза в четырех независимых испытаниях равна, если вероятность появления события в одном испытании равна 0,4 0,1536
Игральная кость бросается 5 раз. Вероятность того, что три очка выпадут 2 раза равна. Ответ округлите до сотых. 0,16
В Машбюро стоит 5 пишущих машин. Вероятность того, что каждая из них в течение года потребуется ремонт 1/5. Вероятность того, что в течение года не придется ремонтировать 2 машины равна 0,0512
Игральная кость подброшена 5 раз. Вероятность того, что один раз появится цифра 6 равна. Ответ округлите до тысячных. 0,402
30% изделий данного предприятия – это продукция высшего сорта. Некто приобрел 6 изделий, изготовленных на этом предприятии. Вероятность, что 4 из них высшего сорта равна. Ответ округлите до сотых. 0.06
Игральная кость бросается 5 раз. Вероятность того, что три очка выпадут 4 раза равна. Ответ округлите до тысячных. 0,003
Всхожесть семян пшеницы оценивается с вероятностью, равной 0,8. Вероятность того, что из 8 посеянных семян взойдет семь равна. Ответ округлите до сотых. 0,34
Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,7. Вероятность того, что при этом будет ровно 5 попаданий равна. Ответ округлите до сотых. 0,32
Вероятность того, что саженец яблони приживется, равна 0,9. Вероятность того, что из десяти саженцев приживутся 8 равна. Ответ округлите до сотых. 0.19
Для одной торпеды вероятность попадания в корабль равна 0.5. Вероятность того, что выпущенные 4 торпеды потопят корабль, если для этого достаточно попадания в цель двух торпед. 0,375
Бросается 5 монет. Какова вероятность того, что три раза выпадет герб. 0.3125
Случайная величина Х принимает значения 7, -2, 1, -5, 3 с равными вероятностями. Математическое ожидание равно 0,8
МХ = 5, МY = 2. Используя свойства математического ожидания, найдите М(2Х – 3Y) 4
DХ = 1.5. Используя свойства дисперсии, найдите D(2X+5) 6
Х и Y - независимы. DX = 5, DY = 2. Используя свойства дисперсии, найдите D(2X+3Y) 38
МХ=1.5. используя свойства математического ожидания, найдите М(2Х+5). 8
Куплено 1000 лотерейных билетов. На 80 из них упал выигрыш по 1 руб., на 20 - по 5 руб., на 10 – по 10 руб. Выберите таблицу, которая описывает закон распределения выигрыша
Возможные значения случайной величины Х таковы: х1=2, х2=5, х3 = 8. Известны вероятности: р(Х = 2) = 0.4; р(Х = 5)= 0.15. Вероятность р(Х = 8). 0,45
Задана таблица распределения случайной величины. Величина С равна 0,3
Задана таблица распределения случайной величины. Вероятность р(х<3) равна  0,625 0,625
Требуется найти математическое ожидание дискретной случайной величины X по заданному закону её распределения, заданному таблично (в первой строке таблицы указаны возможные значения, во второй строке – вероятности возможных значений). 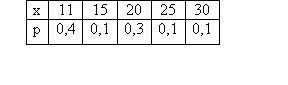 17,4 17,4
Дан закон распределения ДСВ. Дисперсия равна 0,49
Дан закон распределения ДСВ. Средне квадратическое отклонение равно 0,7
Дан закон распределения ДСВ.
x 0 1 2
p 0.2 0.4 0.4
Математическое ожидание равно 1,2
Дан закон распределения ДСВx 0 1 2p 0.2 0.4 0.4. Дисперсия равна 0,56
Дан закон распределения ДСВ
x 0 1 2
p 0.2 0.4 0.4 Средне квадратическое отклонение равно 0,748
Бросаются 2 Монеты. Вероятность того, что выпадут и герб, и решка равна 0,5
Бросаются 2 кубика. Найдите вероятность, что сумма выпавших очков равна 3. Ответ округлите до тысячных. 0,056
В ящике в 5 раз больше красных шаров, чем черных. Найти вероятность р того, что вынутый наугад шар окажется красным. Ответ округлите до тысячных. 0,833
Абонент забыл последнюю цифру номера телефона и поэтому набирает её наугад. Определить вероятность того, что ему придётся звонить не более чем в 3 места. 0,3
Абонент забыл последние 2 цифры телефонного номера, но помнит, что они различны и образуют двузначное число, меньшее 30. С учетом этого он набирает наугад 2 цифры. Найти вероятность того, что это будут нужные цифры. Ответ округлите до тысячных. 0,056
Ребенок имеет на руках 5 кубиков с буквами: А, К, К, Л, У. Вероятность того, что ребенок соберет из кубиков слово "кукла"равна. Ответ округлите до тысячных. 0,017
Брошены три игральные кости. Найти вероятность того, что на двух выпавших гранях появится одинаковое число очков, а на третьей грани - другое число очков. Ответ округлите до тысячных. 0,417
Среди 25 студентов группы, в которой 10 девушек, разыгрывается 5 билетов. Определить вероятность того, что среди обладателей билетов окажутся 2 девушки. Ответ округлите до тысячных. 0,385
На первом этаже семиэтажного дома в лифт зашли 3 человека. Вероятности выхода каждого из лифта на любом этаже одинакова. Найти вероятность того, что все трое вышли из лифта на 4 этаже. Ответ округлите до тысячных. 0,003
Бросают две игральные кости. Определить вероятность того, что на одной кости выпадает 3 очка, на другой 2. Ответ округлите до тысячных. 0,056
Есть колода, состоящая из 52 карт. Из нее случайным образом вынимается четыре карт. Найти вероятность того, что среди них есть две дамы. Ответ округлите до тысячных. 0.025
В группе 15 девушек и 11 парней. Случайным образом выбирают одного студента. Вероятность того, что это юноша равна. Ответ округлите до тысячных. 0,432
Четырёхтомное сочинение расположено на полке в произвольном порядке. Вероятность того, что номера томов идут подряд равна. Ответ округлите до тысячных. 0,083
На экзамен вынесено 60 вопросов, Андрей не выучил 3 из них. Вероятность того, что ему попадется выученный вопрос равна 0,95
В фирме такси в данный момент свободно 20 машин: 10 черных, 2 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Вероятность того, что к ней приедет зеленое такси равна 0,4
В случайном эксперименте симметричную монету бросают дважды. Вероятность того, что орел выпадет ровно один раз равна 0,5
В случайном эксперименте бросают две игральные кости. Вероятность того, что в сумме выпадет 12 очков равна. Ответ округлите до тысячных. 0,028
Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений по одному от каждой страны. В первый день 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Вероятность того, что выступление представителя России состоится в третий день конкура равна. Ответ округлите до тысячных. 0,225
Двойной интеграл в полярных координатах от функции f(r,φ) по области D имеет вид
Тройной интеграл в цилиндрических координатах от функции f(r,φ,z) по области D имеет вид
Тройной интеграл в декартовой системе координат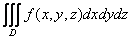
Тройной интеграл в цилиндрической системе координат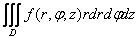
Тройной интеграл в сферической системе координат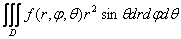
На области D в плоскости XOY задана функция f(x,y)>0, тогда выражает Объём тела, под графиком функции z=f(x,y) над областью D, Массу области D, если считать, что f(x,y) есть плотность вещества на области D
На области D пространства задана функция f(x,y,z)>0, тогда 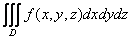 выражает Массу области D, если считать, что f(x,y,z) есть плотность вещества на области D выражает Массу области D, если считать, что f(x,y,z) есть плотность вещества на области D
Квадратная область D в плоскости XOY ограничена прямыми x=0, x=1, y=0,y=1, и разделена прямыми x=0.5, y=0.5 на 4 квадратные части со сторонами Δx=0.5, Δy=0.5. Тогда интегральная сумма для функции f(x,y) на области D может иметь вид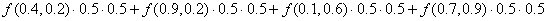 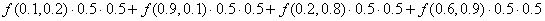 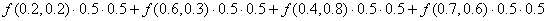
Двойной интеграл есть Число
С помощью двойного интеграла можно находить Площади плоских фигур, Объём трёхмерного тела ,Среднее значение функции двух переменных на области её задания
С помощью двойного интеграла можно находить Массу плоской пластины, Координаты центра масс плоской пластины, Площадь плоской пластины, Объём трёхмерного тела
С помощью тройного интеграла можно находить Массу трёхмерного тела, Объём трёхмерного тела, Среднее значение функции трёх переменных на области её задания
Область D на плоскости XOY является правильной если любая прямая параллельная осям ОХ или ОY и проходящая через внутреннюю точку D пересекает границу D не более чем в двух точках
Изменить порядок интегрирования для  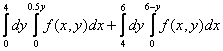
Изменить порядок интегрирования для 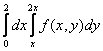
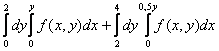
|
 Скачать 0.84 Mb.
Скачать 0.84 Mb.
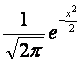 , равны 0; 1
, равны 0; 1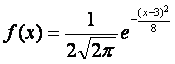
 0,686
0,686  17,4
17,4