высшая математика. 2 13 Случайная величина распределена нормально с параметрами 3 и 2(N3,2). Ее математическое ожидание и дисперсия равны mx 3 dx 4

• Название: 2 13 Случайная величина распределена нормально с параметрами 3 и 2(N3,2). Ее математическое ожидание и дисперсия равны mx 3 dx 4
• Анкор: высшая математика
• Дата: 25.06.2022
• Размер: 0.84 Mb.
• Имя файла: Vysh_Mat_2_kurs_1_semestr.doc
• Тип: Документы; #615116
• страница: 2 из 5

150. Изменить порядок интегрирования для 



151. Изменить порядок интегрирования для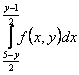 



152. Изменить порядок интегрирования для 



153. Изменить порядок интегрирования для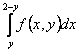  

 

154. Изменить порядок интегрирования для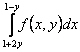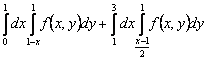 

 

155. Изменить порядок интегрирования для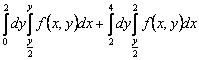 



156. Изменить порядок интегрирования для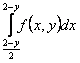 



157. Изменить порядок интегрирования для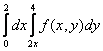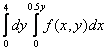 



158. Изменить порядок интегрирования для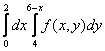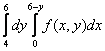 



159. Изменить порядок интегрирования для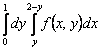  



160. Изменить порядок интегрирования для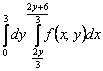 



161. Изменить порядок интегрирования для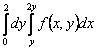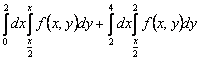 



162. Изменить порядок интегрирования для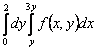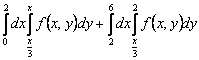 

 

163. Изменить порядок интегрирования для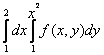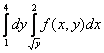 



164. Изменить порядок интегрирования для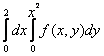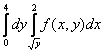 



165. Изменить порядок интегрирования для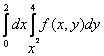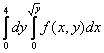 



166. Изменить порядок интегрирования для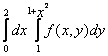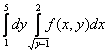 



167.  Изменить порядок интегрирования для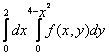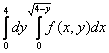 



168.  Изменить порядок интегрирования для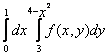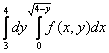 



169. Изменить порядок интегрирования для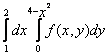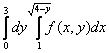 



170. Изменить порядок интегрирования для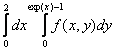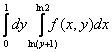 



171. Изменить порядок интегрирования для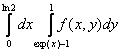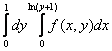 



172.  Изменить порядок интегрирования для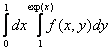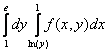 



173. Если D - круг:  , то   равен

174. 
     Если D - круг  , то   равен   
     
175. 
     Если D - круг  , то   равен
     
176. 
     Если D - круг  , то   равен
     
177. 
     Если D - круг  , то   равен
     
178. 
     Если D - круг  , то   равен
     
179. 
     Если D - круг  , то   равен
     
180. 
     Если D - круг  , то   равен
     
181. 
     Если D - круг  , то   равен
     
182. 
     Если D - круг:  , то   равен
     
183. 
     Если D - круг  , то   равен
     
184. 
     Если D - круг  , то   равен
     
185. 
     Если  D-часть  круга:  ,  , то   равен 48
     
186. 
     Если  D- часть круга   , то   равен
     
187. 
     Если  D- часть круга   , то   равен 9
     
188. 
     Если  D - часть круга   , то   равен 45
     
189. 
     Если  D - часть круга   , то   равен 16
     
190. 
     Если  D- часть круга   , то   равен
     
191. 
     Если  D- часть круга   , то   равен
     
192. 
     Если  D- часть круга   , то   равен
     
193. 
     Если  D - кольцо  , то   равен
     
194. 
     Если  D- часть круга   , то   равен
     
195. 
     Если  D- часть круга   , то   равен   
     
196. 
     Если  D- часть кольца   , то   равен 3
     
197. 
     Если область  D ограничена линиями:  x = 0, y =  ,  y=x , то  равен -2
     
198. 
     Если область  D ограничена линиями: x = 0,  y = 2 ,  y = x, то   равен
     
199. 
     Если область  D ограничена линиями: y = x + 4 , x = 4, y = 4-x, то  равен
     
200. 
     Если область  D ограничена линиями: y+ x =2 ,   x=4, y=4 ,то  равен
     
201. 
      Если область  D ограничена линиями:   x=1,  x=4,  y=x,  y=2x, то   равен
     
202. 
     Если область  D ограничена линиями: x=1, y=x², y= 0, то   равен
     
203. 
     Если область  D ограничена линиями: x=2,  y=x²,  y= 0, то   равен   
     
204. 
     Если область  D ограничена линиями: x=1,   y=x³,   y=0, то   равен   
     
205. 
     Если область  D ограничена линиями: x=0, x= , y=0,y=1, то   равен 1
     
206. 
     Если область  D ограничена линиями: x=1, y=x², y=0, то   равен
     
207. 
     Если область  D ограничена линиями: x=1,   x=2, y=x³,   y=0, то   равен 255
     
208. 
     Если область  D ограничена линиями:  1 x 3,     y , то   равен 12
     
209. 
     Если область  D ограничена линиями:  x=1,  x=3,  y= ,  y= , то   равен -1
     
210. 
     Если область  D ограничена линиями:  x=2,   y=x,   y=2x, то   равен
     
211. 
     Если область  D ограничена линиями:     y=0,   y=  , то   равен
     
212. 
     Если область  D ограничена линиями:   y=4x,   x=1, y=x, то   равен 5
     
213. 
     Если область  D ограничена линиями:   y=2x,   x+y=0,   x=3 , то   равен 4,5
     
214. 
     Если область  D ограничена линиями:   x=1,   y=0,   y=2x, то   равен
     
215. 
     Если область  D ограничена линиями:   y=2,   x = y,   x  =0, то   равен
     
216. 
     Если область  D ограничена линиями:   0 ,   0  , то   равен   
     
217. 
     Если область  D ограничена линиями:   x=0,   y=2,   y= x+1,то   равен
     
218. 
     Если область  D ограничена линиями: x=2,  y=x,  y=2x, то   равен 3
     
219. 
     Если область  D ограничена линиями: x=0,  x=2,  y= ,  y=  , то   равен 1
     
220. 
     Если область  D ограничена линиями:  1 x 2,     y , то   равен 6
     
221. 
     Повторный интеграл     равен 0
     
222. 
     Повторный интеграл    равен 4
     
223. 
     Повторный интеграл    равен 0
     
224. 
      Повторный интеграл    равен 1
     
225. 
     Повторный интеграл    равен 1
     
226. 
     Повторный интеграл 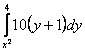   равен 159
     
227. 
     Повторный интеграл    равен 11
     
228. 
     Повторный интеграл    равен 271
     
229. 
     Повторный интеграл    равен 2
     
230. 
     Повторный интеграл     равен 88
     
231. 
     Повторный интеграл     равен 2
     
232. 
     Повторный интеграл    равен 11
     
233. 
     Повторный интеграл     равен 14
     
234. 
     Повторный интеграл    равен 1
     
235. 
     Повторный интеграл     равен 5
     
236. 
     Повторный интеграл    равен 125
     
237. 
     Повторный интеграл    равен 16
     
238. 
     Повторный интеграл    равен 1
     
239. 
     Повторный интеграл    равен 7
     
240. 
     Повторный интеграл    равен 40
     
241. 
     Повторный интеграл    равен 13
     
242. 
     Повторный интеграл    равен 1
     
243. 
     Повторный интеграл    равен 3
     
244. 
     Повторный интеграл    равен 3
     

245.Повторный интеграл    равен 3

246.Из нижеперечисленных выберите признак Даламбера  , ряд сходится при   и расходится при  .

247. Числовым рядом называется выражение вида…



248. Выберите из нижеперечисленных достаточный признак расходимости ряда.

         

249. Из нижеперечисленных выберите достаточный признак сходимости знакопеременного ряда. если сходится ряд, составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд.

250. Из нижеперечисленных выберите формулу радиуса сходимости ряда

251. Функцианальным рядом называется выражение вида…

252. Выберите из нижеперечисленных необходимый признак сходимости ряда

253. Из нижеперечисленных выберите признак сравнения 3.  ,        ,      ,  если В сходится, то А сходится; если А расходится, то и В расходится.

254. Знакопеременный ряд называется абсолютно сходящимся, если… ряд, составленный из модулей его членов, сходится

255. Из нижеперечисленных выберите верные утверждения. «Ряды применяются для…» приблеженного вычисления значения функции, приближенного решения дифференциальных уравнений, приближенного вычисления определенных интегралов

256. Степенным рядом называется выражение вида

257. Из нижеперечисленных выберите достаточные признаки сходимости ряда ,

258. Из нижеперечисленных выберите радикальный признак Коши , ряд сходится при   и расходится при  .

259. Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей  его членов, расходится

260. Из нижеперечисленных выберите достаточные признаки расходимости ряда ,,,,, ,,,,,

261. Из нижеперечисленных выберите интегральный признак Коши : если   сходится (расходится), то и ряд   сходится (расходится).

262. Из нижеперечисленных выберите формулу радиуса абсолютной сходимости степенного  ряда

263. Из нижеперечисленных выберите признак Лейбница Если U₁>U₂>U₃…>U_n>…        и  , то ряд  сходится

264. Знакочередующимся рядом называется выражение вида…

265. Из нижеперечисленных выберите достаточные признаки сходимости признак сравнения, признак Даламбера, радикальный признак Коши, интегральный признак Даламбера

266. Из нижеперечисленных выберите формулу радиуса сходимости ряда

267. Выберите из ниже перечисленных знакопеременный ряд  ;

268. Выберите из ниже перечисленных знакоположительный ряд:

269. Выберите из ниже перечисленных степенной ряд:

270. Выберите из ниже перечисленных ряд Фурье

271. Выберите из ниже перечисленных функциональный ряд:  

272. К какому типу относится данный ряд  ряд Фурье 

273. К какому типу относится данный ряд  степенной ряд 

274. К какому типу относится данный ряд  знакопеременный ряд

275. К какому типу относится данный ряд  степенной ряд ,,,,,функциональный ряд

276. В ряд Фурье разлагаются функции, описывающие … периодические процессы

277. Рядом Фурье называется выражением вида… 4. 

278. Для того чтобы ряд Тейлора сходился в точке х, необходимо  и достаточно, чтобы…

279. Из нижеперечисленных выберите формулу, по которой вычисляется коэффициент a_n для ряда Фурье с периодом 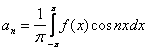<sub>¤    

280.</sub> Из нижеперечисленных выберите формулу, по которой вычисляется коэффициент b_n для ряда Фурье с периодом 2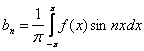

281. Формула Тейлора имеет вид

282. Ряд Тейлора имеет вид

283. Если раскладываемая в ряд Фурье функция является четной, то коэффициент а₀ равен:

284. Если раскладываемая в ряд Фурье функция является нечетной, то коэффициент а₀ равен:

285. Если раскладываемая в ряд Фурье функция является функцией общего вида, то коэффициент а₀ равен: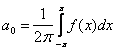

286. Если раскладываемая в ряд Фурье функция является четной, то коэффициент а_n равен: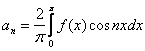

287. Если раскладываемая в ряд Фурье функция является нечетной, то коэффициент а_n равен:

288. Если раскладываемая в ряд Фурье функция является функцией общего вида, то коэффициент а_n равен: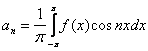

289. Если раскладываемая в ряд Фурье функция является четной, то коэффициент b_n равен:

290. Если раскладываемая в ряд Фурье функция является нечетной, то коэффициент b_n равен: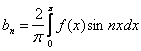

291. Если раскладываемая в ряд Фурье функция является функцией общего вида, то коэффициент b_n равен: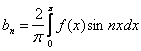

292. Если раскладываемая в ряд Фурье функция является функцией общего вида, то ее разложение в тригонометрический ряд имеет вид:

293. Если раскладываемая в ряд Фурье функция является нечетной, то ее разложение в тригонометрический ряд имеет вид:

294. Если раскладываемая в ряд Фурье функция является четной, то ее разложение в тригонометрический ряд имеет вид:

295. Разложить в ряд Тейлора функцию f(x)=xln(1+x²)  по степеням х

296. Разложить в ряд Фурье функцию 

297. Разложить в ряд Маклорена функцию  

298. Разложить в ряд Фурье функцию  

299. Разложить в ряд Маклорена функцию   

300. Разложить в ряд Фурье функцию 

301. Разложить в порядке Тейлора функцию 

302. Разложить в ряд косинусов функцию