2.А._пк2. 2. А. П фирма фирма. Цели фирмы Производственная функция и ее характеристики Равновесие (оптимум) фирмы
 Скачать 1.96 Mb. Скачать 1.96 Mb.
|
Рынок трудаЗадача 1 Фирма продает некий продукт на совершенно конкурентном рынке по 10 руб. за штуку. Производственная функция имеет вид: Q = 145L –0,75L2 , где Q – объем производства, L – количество работников. Ставка заработной платы W = 1000руб. в месяц. Определить оптимальное количество работников. Решение:Находим MRPL = Р*МPL = 10*(145 - 2*0,75L) =1450 - 15L = W = 1000; L = 30Задача2.В фирме “Надувательство”, по надуванию воздушных шариков работают 3 человека, причем каждый надувает в среднем 198 шариков в день. После того как фирма наняла еще одного работника, общее количество надуваемых шариков возросло на 66. Что произошло со средней производительностью труда?Решение:Поскольку предельный продукт труда (66 дополнительных шариков) меньше среднего продукта труда (198 шариков), то средняя производительность труда понижается.Задача 3.В некоторой малой фирме работают двое рабочих, получающих в месяц по 4 тыс. руб. и президент, получающий 10 тыс.руб. в месяц. Как изменилась средняя зарплата на фирме после того, как наняли бухгалтера, работающего за 6 тыс.руб. в месяц?Решение:Средняя зарплата в фирме ранее была равна (2.4+10)/3 = 6 тыс.руб.После найма бухгалтера средняя зарплата стала (2*4+6+10)/4 = 6 тыс.руб.Таким образом, средняя зарплата не изменилась.Задача4. Фирма “Перпетум мебели” уволила 30% работников, а оставшимся подняла зарплату на 30%. При этом объем производства мебели вырос на 40%.
Решение:
Число работников сократилось на 30%, то есть L2 =0,7L1 Производительность труда стала равнойQ2/L2 =(1,4Q1/ 0,7L1) = 2 Q1/ L1, то есть выросла в 2 раза.b) Зарплата каждого работника увеличилась на 30%, то естьW2 = 1,3 W1.Затраты фирмы на оплату труда стали равными L2 W2 =0,7L 1*1,3W 1 =0,91L1 W1 , то есть сократились на 9%Ответ: производительность труда выросла в 2 раза, а затраты фирмы на оплату труда сократились на 9%Рынок капиталаФормулы, применяемые при решении задач: Ставка процента –i = I/K , где i - ставка ссудного процента, I – годовой доход от кредита, K – первоначальная сумма кредита. 2. Простые ставки ссудных процентов: S = P (1+n i), где Р - первоначальная сумма кредита, i - ставка ссудного процента, n – период начисления. 3. Дисконтирование – по наращенной сумме S, периоду начисления n и простой процентной ставке i нужно определить первоначальную сумму P, т.е. P = S : (1+n i). 4. Сложные ставки ссудных процентов: S = P (1+ i) n . 5 Дисконтирование – по наращенной сумме S, периоду начисления n и сложной процентной ставке i нужно определить первоначальную сумму P, т.е. P = S : (1+ i)n . 6. Методы оценки инвестиционных решений : А) метод чистой приведенной стоимости : 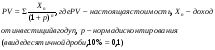 Б) метод нормы внутренней отдачи: норма дисконтирования, при которой настоящая стоимость инвестиций равна 0. Задача1. Первоначальная сумма Р = 5000руб. Помещена в банк на n=2 года под i = 15% годовых (простые проценты). Найти наращенную сумму. Решение: наращенная сумма после двух лет S = P (1+n i) = 5000 (1 + 2*0.15) = 6500 Задача2. Первоначальная сумма Р = 3000 руб., наращенная сумма S = 4500руб., i = 20% годовых (простые проценты). Найти период начисления. Решение: Из формулы S = P (1+n* i) находим n = (S – P) : (i *P) = (4500 – 3000) : 0,2*3000 = 2,5 года. Задача 3. Первоначальная сумма Р = 2000 руб., наращенная сумма S = 2200руб., период начисления n = 0,5 года. Найти простую процентную ставку. Решение: Из формулы S = P (1+n* i) находим i = (S – P) : (n* P) = 0,2 (20%). Задача 4(дисконтирование). Наращенная сумма S = 7000руб., период начисления n = 0,25 года (один квартал), простая процентная ставка i = 15% годовых. Найти первоначальную сумму. Решение: Из формулы S = P (1+n* i) находим Р = S : (1+n* i) = 7000 : (1 +0.25*0,12) = 6796,12 руб. Задача 5. .Первоначальная сумма Р = 7000руб. помещена в банк на n = 3 года под i = 10% годовых (сложные проценты). Найти наращенную сумму. Решение: наращенная сумма после трех лет S = P (1+ i)n = 7000 (1 + 0.15)3 = 10646руб. Задача 6(дисконтирование). Наращенная сумма S = 7000руб., период начисления n = 2 года, сложная процентная ставка i = 12% годовых. Найти первоначальную сумму. Решение: Из формулы S = P (1+ i)n находим Р = S : (1+ i)n = 7000 : (1 +0,12)2 = 5580,36руб. Задача7.Предприятие анализирует два инвестиционных проекта на 2 млн. руб. Оценка чистых денежных вложений приведена в таблице. Альтернативные издержки по инвестициям равны 12%. Определить чистую приведенную стоимость каждого проекта.
|

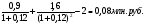
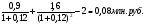
 0,5
0,5