Курсовая работа по теории механизмов и машин. схема 59-12 — часть 2 силы. 2 кинематический анализ рычажного механизма 1 исходные данные
 Скачать 35.46 Kb.
|
|
2 кинематический анализ рычажного механизма 2.1 ИСХОДНЫЕ ДАННЫЕ 2.1.1 Кинематическая схема 2.1.2 Дополнительно определенный размер lЕС =0,87м. 2.1.3 Угловая скорость кривошипа 1 ω1= ωк =8рад/с. 2.1.4 Угол поворота кривошипа от начального положения до расчетного φп=70°. 2.2 определение положений звеньев и некоторых точек 2.2.1 Для построения планов механизма принимаем масштаб длины µl =0,004м/мм и вычисляем чертежные размеры звеньев: 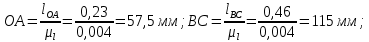 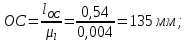 2.2.2 Строим план механизма в расчетном положении, повернув кривошип от положения «Н» на угол φп в сторону вращения. Отмечаем полученные точки верхними индексами «п». 2.2.3 Измеряем угол размаха кулисы, а также угол ее поворота из начального положения в расчетное: ψ=50,42°; ψр=12,15°. 2.3 определение скоростей 2.3.1 Линейная скорость конца кривошипа: 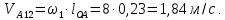 2.3.2 Абсолютная скорость т. 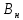 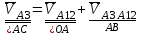, если рассматривать ее как точку шатуна: по ω1 2.3.3 Принимаем масштаб скорости µV =0,01м/c·мм. Решаем уравнение графически. Длина вектора 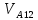 : 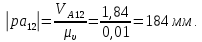Определяем искомые линейные скорости: 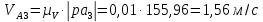 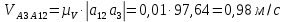 2.3.4 Находим величину угловой скорости звена 3. С этой целью предварительно, определяем расстояния между центрами шарниров А и С, измерив его на плане механизма. 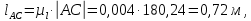 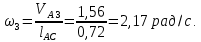 Направление – по часовой стрелки. 2.3.5 Вычисляем линейную скорость точки В: 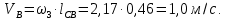 Длина соответствующего ей вектора на плане скоростей 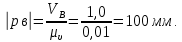 Направление – перпендикулярно СВ в сторону  .2.4 определение ускорений 2.4.1 Ускорение центра шарнира А 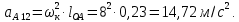 2.4.2 Рассматривая вращательное движение кулисы 3 и сложное движение, лежащей на ней точки А3 , взяв в качестве исходных центры шарниров А12 и С, составляем систему векторных уравнений точки А3 и анализируем входящие в уравнения векторы. 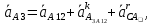 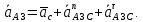 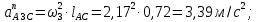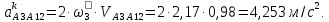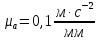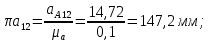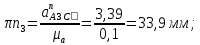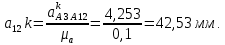2.4.3 Вычисляем нормальную составляющую ускорения точки А3, а также величину ускорения Кориолиса:   2.4.4 Принимаем масштаб плана ускорений  и вычисляем длины векторов на чертеже:   2.4.5 Решаем систему графически. Точку bнаходим с использованием теоремы о подобии для плана ускорений звена 3. В каждом положениипрямойa3cbна плане ускорений должен быть подобен прямой АСВ на плане механизма. Поэтому соответствующие их стороны должны быть пропорциональны. Составляем пропорцию и, решая, определяем искомую длину отрезка на чертеже. Для построения точки b составляем и решаем пропорцию: 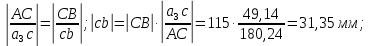 2.4.6 Измерив соответствующие векторы, находим величины тангенциальной составляющей ускорения точки А3. 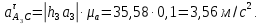 2.4.7 Вычисляем значение углового ускорения кулисы 3: 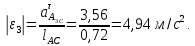 2.4.8 Используя теорему о подобии для ускорений звена 3, наносим на планы концы вектора ускорения центра масс стержня ВЕ - точка 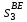 . 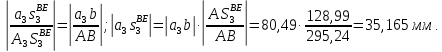2.4.12 Вычерчиваем эти векторы, измеряем их длины и вычисляем численные величины этих ускорений: 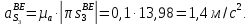 3 Cиловой анализ рычажного механизма 3.1 ИСХОДНЫЕ ДАННЫЕ 3.1.1 Результаты кинематического анализа механизма. 3.1.2 Направление и точка приложения силы полезного сопротивления 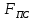 3.1.3 Величина силы полезного сопротивления 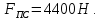 3.1.5 Удельная масса звеньев q=30кг/м. 3.2 Определение сил веса и инерционной нагрузки, действующих на звенья 3.2.1 Находим массы звеньев: 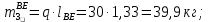 Массами звеньев 1 2 пренебрегаем ввиду малости. 3.2.2 Вычисляем силы веса звеньев: 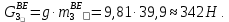 Здесь и далее величины сил округляем с точностью до 1Н. 3.2.3 Находим силы инерции звеньев в расчетном положении: 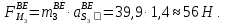 3.2.4 Вычисляем момент инерции стержней, составляющих звено 3 относительно их центров масс.  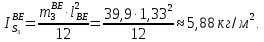 3.2.5 Находим момент пары сил инерции, действующий на звено 3 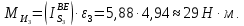 Направление по часовой стрелке. 3.3 Силовой расчет механизма методом планов сил 3.3.1 Приняв масштаб длины µl =0,004м/мм, строим планы структурной группы 2-3 и входного звена. Чертежные размеры звеньев: 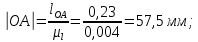 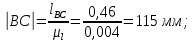 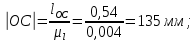 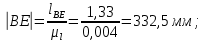 3.3.2 Наносим на план механизма все активные силовые факторы, а также инерционную нагрузку, действующие на звенья механизма. Кривошип 1 считаем сбалансированным. Поэтому инерционная нагрузка на него отсутствует. 3.3.3 На план структурной группы 2-3, кроме силовых факторов, указанных в п. 3.3.2, наносим реакции со стороны звена 1 и стойки. Реакция 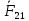 в шарнире С неизвестна как по величине, так и по направлению. Линию действия 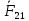можно установить , рассмотрев кинетостатическое равновесие звена 2. Уравнение кинетостатики 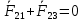 Отсюда 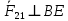 Направление вектора этой силы указываем произвольно. 3.3.4 Составляем и анализируем векторное уравнение кинетостатики для всей структурной группы 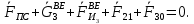 Оно содержит 2 неизвестные величины и не поддается прямому графическому решению. 3.3.5 Вычисляем величину и определяем направление реакции 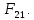 C этой целью составляем и решаем уравнение моментов относительно центра шарнира С.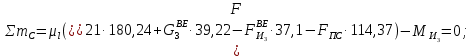 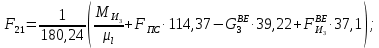 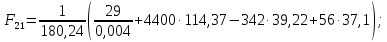 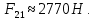 3.3.6 Для графического решения векторного уравнения принимаем масштаб плана сил µF =24 Н/мм и вычисляем длины отрезков, соответствующие каждой силе на плане: 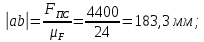 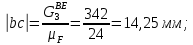 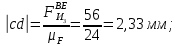 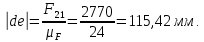 3.3.7 Cтроим план сил и по нему определяем искомую реакцию: 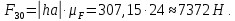 3.3.8 Составляем, анализируем и в масштабе сил µF = 20Н/мм решаем графически векторное уравнение кинетостатики звена 1. 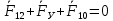 Длине на плане полностью известного вектора 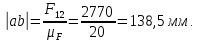 Искомые силы: 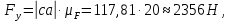 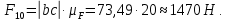 3.4 Определение уравновешивающей силы методом рычага жуковского 3.4.1 Раскладываем момент пары сил инерции, действующий на звено 3, на пару сил, используя зависимость: 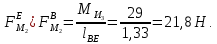 3.4.2 Взяв план скоростей из кинематического анализа механизма, чертим его, повернув на 90°. Для построения на планах точек используем теорему о подобие для плана скоростей звена 3. С этой целью используем масштабирование так же, как в пункте 2.4.8, но отрезки измеряем на плане скоростей. Для построения точки е составляем и решаем пропорцию: 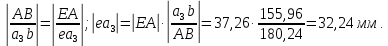 3.4.3 К соответствующим точкам плана прикладываем действующие на звенья силы. Получили рычаг Жуковского. 3.4.4 Составляем уравнение моментов относительно полюса и находим из него уравновешивающую силу. 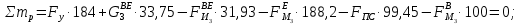 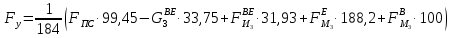 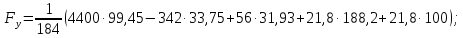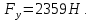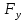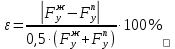;  3.4.5 Относительная погрешность определения  разными способами где 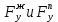 – величины уравновешивающей силы, определенные методами рычага Жуковского и планов сил соответственно.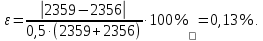 Расхождение не превышает 5%. Расчет выполнен правильно обоими методами. |