2. Понятие функции. Основные свойства функций
 Скачать 320.74 Kb. Скачать 320.74 Kb.
|
6.3. Замечательные пределыК пределам 4-го типа отнесем примеры с неопределенностью вида 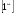 . В этом случае выражение, стоящее под знаком предела, представляет собой степенно-показательную функцию, в основании которой необходимо выделить целую часть дроби (которая должна быть равна 1). Неопределенность устраняется при помощи выделения «второго замечательного предела» . . В этом случае выражение, стоящее под знаком предела, представляет собой степенно-показательную функцию, в основании которой необходимо выделить целую часть дроби (которая должна быть равна 1). Неопределенность устраняется при помощи выделения «второго замечательного предела» .При нахождении пределов могут встретиться неопределенности вида Эти случаи путем преобразования функции приводятся к одному из двух рассмотренных случаев, т.е. к неопределенностям вида Примеры. 1. Найти При 8. Непрерывность функции в точке и на отрезке (2 определения) Функция Функция Эти два определения непрерывности функции в точке равносильны друг другу. Функция называется непрерывной в интервале, если она непрерывна во всех точках этого интервала. 9. Дифференциальное исчисление функции 1 переменной. Производная функции Основ-ные правила дифференцирования. Производной функции Если Функция, имеющая конечную производную называется дифференцируемой. Операция нахождения производной называется дифференцированием. Геометрическое значение производной. Производная функция Быстрота протекания физических, химических и других процессов выражается с помощью производной. Если 10. Производные степенных, тригонометрических, показательных, логарифмических функций. Производная сложной функции. Основные формулы: Если Основные формулы: Если Основные формулы: Для сложных функций 11. Производные обратных тригонометрических функций. Производные высших порядков. Производной второго порядка или второй производной функции Аналогично определяются и обозначаются производные третьего, четвертого и других порядков: Формула Лейбница для производной Производные п-го порядка называется производная от производной 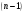 -го порядка. Производные высших порядков вычисляются последовательным дифференцированием данной функции: -го порядка. Производные высших порядков вычисляются последовательным дифференцированием данной функции: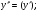 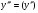 ; …; ; …; 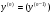 . (7.28) . (7.28)Если функция задана параметрически, то 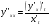 ; ; 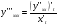 ; …; ; …;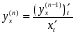 . .12. Экономический смысл производной. Использование понятия производной в экономике. 1. Предельные величины. Применение производной в экономике позволяет получать так называемые предельные характеристики экономических объектов или процессов. Предельные величины (предельная выручка, полезность, производительность, предельный доход, продукт и др.) характеризуют не состояние, а скорость изменения экономического объекта или процесса по времени или относительно другого исследуемого фактора. Издержки производства. Если издержки производства 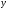 рассматривать как функцию выпускаемой продукции рассматривать как функцию выпускаемой продукции  , т.е. , т.е. 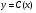 , то , то 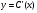 будет выражать предельные издержки производства и приближенно характеризовать прирост переменных затрат на производство дополнительной единицы продукции. Средние издержки являются издержками на единицу выпуска продукции: будет выражать предельные издержки производства и приближенно характеризовать прирост переменных затрат на производство дополнительной единицы продукции. Средние издержки являются издержками на единицу выпуска продукции: 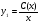 . .2. Производительность труда. Пусть функция 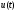 выражает объем произведенной продукции выражает объем произведенной продукции 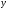 за время за время 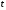 . Тогда производная объема произведенной продукции по времени . Тогда производная объема произведенной продукции по времени 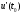 есть производительность труда в момент есть производительность труда в момент 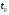 . .3. Функция потребления и сбережения. Если  - национальный доход, - национальный доход, 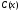 - функция потребления (часть дохода, которая тратится), а - функция потребления (часть дохода, которая тратится), а 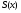 - функция сбережения, то - функция сбережения, то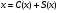 . (7.33) . (7.33)Дифференцируя, получим, что 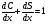 , (7.34) , (7.34)где 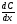 - предельная склонность к потреблению; - предельная склонность к потреблению; 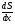 - предельная склонность к сбережению. - предельная склонность к сбережению.4. Эластичность. Эта мера реагирования одной переменной величины на изменение другой. Эластичность функции приближенно показывает, на сколько процентов изменится одна переменная в результате изменения другой переменной на 1%. Эластичность функции определяется с помощью соотношения: 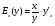 или или 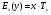 , (7.35) , (7.35)где 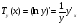 (7.36) (7.36)– относительная скорость изменения (темп) функции. Эластичность функции применяется при анализе спроса и предложения от цены (ценовая эластичность). Она показывает реакцию спроса или предложения на изменение цены и определяет, на сколько процентов приближенно изменится спрос или предложение при изменении цены на 1%. Если эластичность спроса 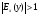 , то спрос считается эластичным, если , то спрос считается эластичным, если 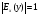 – нейтральным (с единичной эластичностью), а если – нейтральным (с единичной эластичностью), а если 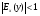 – неэластичным относительно цены. – неэластичным относительно цены.13. Дифференциал и его свойства. Приложение производной. Правило Лопиталя - Бернулли. Дифференциалом функции В частности, при Формулу (21) можно, следовательно, написать так Дифференциал функции Из определения производной и дифференциала вытекает, что где При малых Если |
