2. Понятие функции. Основные свойства функций
 Скачать 320.74 Kb. Скачать 320.74 Kb.
|
|
16. Общая схема исследования функции. Исследование функции можно проводить по следующей схеме: 1. Найти область существования функции. 2. Исследовать изменения функции при 3. Найти промежутки возрастания и убывания функции, точки экстремума. 4. Вычислить значения экстремумов. 5. Определить интервалы выпуклости и вогнутости графика, найти точки перегиба. 6. Найти точки пересечения графика с координатными осями. 7. Найти асимптоты графика функции. По результатам исследования можно построить математически грамотный эскиз ее графика. Если исследуемая функция четная или нечетная, достаточно исследовать функцию и построить ее график для положительных значений аргумента из области определения. Иногда порядок исследования целесообразно выбирать, исходя из конкретных особенностей данной функции. 17. Неопределенный интеграл и его свойства. Неопределенным интегралом от непрерывной функции 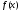 или от дифференциального выражения или от дифференциального выражения 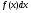 называется общее выражение для всех первообразных функций называется общее выражение для всех первообразных функций 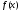 .Обозначение: .Обозначение: 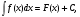 (1) (1)где 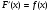 . Функция . Функция 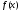 называется подынтегральной функцией, а выражение называется подынтегральной функцией, а выражение 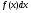 - подынтегральным выражением. - подынтегральным выражением.Свойства неопределенного интеграла. 1. Производная неопределенного интеграла равна подынтегральной функции; дифференциал неопределенного интеграла равен подынтегральному выражению: 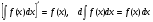 . (2) . (2)2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной: 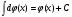 . (3) . (3)3. Постоянный множитель можно выносить за знак неопределенного интеграла: 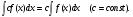 (4) (4)4. Неопределенный интеграл от алгебраический суммы непрерывных функций равен такой же алгебраической сумме неопределенных интегралов от слагаемых: 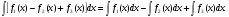 Таблица простейших неопределенных интегралов 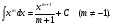 (5) (5) 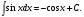 (10) (10)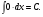 (5а) (5а) 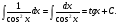 (11) (11)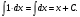 (5б) (5б) 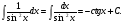 (12) (12)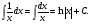 (6) (6)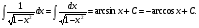 (13) (13)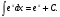 (7) (7) 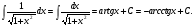 (14) (14)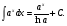 (8) (8) 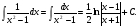 (15) (15)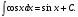 (9) (9)1. Производная неопределенного интеграла равна подынтегральной функции; дифференциал неопределенного интеграла равен подынтегральному выражению: 2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной: 3. Постоянный множитель можно выносить за знак неопределенного интеграла: 4. Неопределенный интеграл от алгебраической суммы непрерывных функций равен такой же алгебраической сумме неопределенных интегралов от слагаемых: Таблица простейших неопределенных интегралов 18. Методы интегрирования: интегрирование разложением. Метод подстановки. Метод разложения основан на свойстве 4 неопределенного интеграла. Если Интегрирование путем введения новой переменной (метод подстановки) основано на формуле где Примеры. 1. Найти интеграл Положим 19. Методы интегрирования: метод интегрирования по частям. Если получается формула интегрирования по частям Эта формула применяется в случае, когда подынтегральная функция представляет произведение алгебраической и трансцендентной функции. В качестве В некоторых случаях для сведения данного интеграла к табличному формула (18) применяется несколько раз. Иногда искомый интеграл определяется из алгебраического уравнения, получающегося с помощью интегрирования по частям. |
