2. Понятие функции. Основные свойства функций
 Скачать 320.74 Kb. Скачать 320.74 Kb.
|
|
Глава 3. Приложения производной. Понятие производной находит многочисленные приложения. С помощью производной можно найти касательную к кривой в данной точке, найти скорость и ускорение неравномерного движения в данный момент времени. Производная широко применяется при исследовании функций, являющихся переменными величинами. С переменными же величинами постоянно встречаются при изучении закономерностей природы. Правило Лопиталя-Бернулли является эффективным средством нахождения предела функции в тех случаях, когда аргумент неограниченно возрастает или стремится к значению, которое не входит в область определения функции. I. Раскрытие неопределенностей вида Пусть функции Если Последняя формула и выражает правило Лопиталя-Бернулли: предел отношения двух бесконечно малых или бесконечно больших величин равен пределу отношения их производных, если последний существует или равен бесконечности. Правило это применимо и в случае, когда Замечание 1. Предел отношения функций может существовать в то время, когда отношения производных не стремятся ни к какому пределу. II. Раскрытие неопределенностей вида 1. Для раскрытия неопределенности вида 2. В случае неопределенности вида и раскрыть сначала неопределенность 3. Неопределенности видов Замечание 2. Выражение "раскрыть неопределенность типа В некоторых случаях правило Лопиталя-Бернулли полезно комбинировать с нахождением пределов элементарными способами. 14. Возрастание и убывание функции. Экстремум функции. Н. и д. условия экстремума. Наибольшее и наименьшее значение функций. 2. Точка x0 называется точкой максимума (минимума) функции y = f(x), если существует интервал, содержащий точку x0, такой, что для всех x из этого интервала имеет место неравенство f(x0) ≥f(x), (f(x0) ≤ f(x)). Точки максимума и точки минимума называются точками экстремума. 3. Необходимое условие экстремума: в точке экстремума функции ее производная либо равна нулю (f′(x)=0), либо не существует. 4. Первое достаточное условие экстремума: если в точкеx0 функция y = f(x) непрерывна, а производнаяf′(x) при переходе через точку x0 меняет знак, то точка x0 – точка экстремума: максимума, если знак меняется с «+» на «-», и минимума, если с «–» на «+». Если при переходе через точку x0 производная не меняет знак, то в точке x0 экстремума нет. 5. Второе достаточное условие экстремума: если в точке x0 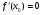 , а , а 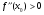 , то x0 является точкой максимума функции. Если , то x0 является точкой максимума функции. Если 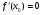 , а , а 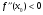 , то x0 является точкой минимума функции. , то x0 является точкой минимума функции.Функция называется возрастающей в некотором промежутке (рис.2, а), если для любых Функция называется убывающей (рис. 2, б) в некотором промежутке, если для любых Достаточное условие возрастания (убывания) функции: если в данном промежутке производная данной функции положительна, то функция в этом промежутке возрастает; если производная данной функции в данном промежутке отрицательна, то функция в этом промежутке убывает. Максимумом функции где Минимумом функции где Максимум или минимум функции называется экстремумом функции. Точки, в которых достигается экстремум, называются точками экстремума. Функция может иметь экстремум только в тех точках области ее определения, в которых производная равна нулю или не существует. Такие точки называются критическими точками аргумента функции. Наименьшее и наибольшее значения непрерывной функции Достаточное условие экстремума. Первое правило. Если в точке 1) функция имеет максимум в точке 2) функция имеет минимум в точке Второе правило. Если в точке 1) 2) Замечание. Пусть первая из неравных нулю в точке 15. Выпуклость и вогнутость функций. Н. и д. условия выпуклости и вогнутости. Асимптоты функции. 1. Функция 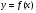 называется выпуклой вверх (вниз) на промежутке, если для любых двух значений x1, x2 из этого промежутка выполняется неравенство называется выпуклой вверх (вниз) на промежутке, если для любых двух значений x1, x2 из этого промежутка выполняется неравенство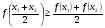 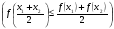 . .Точки, разделяющие интервалы выпуклости, называются точками перегиба. 2. Если вторая производная  f"(x) функции f"(x) функции 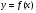 положительна (отрицательна) на промежутке, то функция является выпуклой вниз (вверх) на этом промежутке. положительна (отрицательна) на промежутке, то функция является выпуклой вниз (вверх) на этом промежутке.3. Если x0 – точка перегиба функции 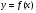 и и  f"(x0) существует, то f"(x0) существует, то  f"(x0) = 0. f"(x0) = 0.4. Если вторая производная f"(x) меняет знак при переходе через точку x0, то точка x0 является точкой перегиба функции 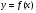 . .Таким образом, функция выпукла вниз на всем интервале (- ∞; 1), и точка х = 0 не является точкой перегиба. Не трудно увидеть, что это точка экстремума (максимума) функции. Точка х = 1 является точкой перегиба. На интервале (1; + ∞) функ ция является выпуклой вниз. 1. Прямая lназывается асимптотой графика функции у = ƒ(х), если расстояние от точки (х, ƒ(х)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. Асимптоты бывают вертикальными, горизонтальными и наклон ными. 2. Прямая х = xоявляется вертикальной асимптотой графика функции у= ƒ(х), если хотя бы один из пределов 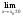 ƒ(х) (правосторонний или левосторонний) равен ƒ(х) (правосторонний или левосторонний) равен 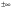 . .Прямая х = xо может быть вертикальной асимптотой функции y = ƒ(х) в том случае, если xо – точка разрыва или граничная точка области определения. 3.Прямая у = bявляется горизонтальной асимптотой, если lim ƒ(х) = b. 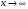 Если lim ƒ(х) = b, то у = b — правосторонняя горизонтальная асимптота, 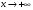 если lim ƒ(х) = b, то у = b — левосторонняя горизонтальная асимптота. 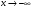 4. Если 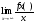 =k =k  0 и 0 и 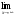 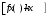 = b, то прямая y = kx + b является наклонной асимптотой графика функции y= ƒ(х). = b, то прямая y = kx + b является наклонной асимптотой графика функции y= ƒ(х). |
