записка. 2. расчетноконструктивный раздел
 Скачать 137.2 Kb. Скачать 137.2 Kb.
|
|
Изм. Лист № докум. Подпись Дата Лист ДП 2-70 02 01-01-2018-ТС-41 КР 2. РАСЧЕТНО-КОНСТРУКТИВНЫЙ РАЗДЕЛ2.1 Расчет железобетонной ребристой плиты покрытия 2.1.1 Исходные данные Для изготовления плиты перекрытия принимаем: бетон класса С20/25; fск=20 МПа; fсtк=1,5 МПа; Еc=36×103 МПа; продольную арматуру – из стали класса S400, fyd=367 МПа; поперечную арматуру из S240, fyd=218 МПа; сварные сетки в верхней и нижней полках из проволоки класса S500, fyd=450 МПа. 2.1.2 Определение нагрузок Таблица 2.1 Сбор нагрузок на 1 м2 плиты покрытия
2.1.3 Расчет полки Расстояние между осями поперечных ребер равно 0,99 м. Расстояние между ребрами в свету или пролет полки плиты l1=990-120=860 мм=0,86 м. Расстояние между продольными ребрами плиты в свету или пролет полки плиты l1=2980-2×155=2670 мм=2,67 м. Отношение пролетов полки плиты l2/l1=2,67/0,86=3,1>3, поэтому полки рассчитываем как многопролетную балочную плиту с расчетным пролетом leff=l1=0,86 м. Для расчета вырезаем полосу шириной b=1,0 м. Толщина полки или высота сечения h=30 мм, тогда рабочая высота сечения d=h/2=30/2=15 мм. Полная расчетная нагрузка на полку плиты с учетом только собственного веса полки составит: qn=(1,2+1,2+25×43,2×1,35)×1,0=1460,4 кН/м. Расчетный изгибающий момент от этой нагрузки Msd= 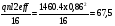 кН×м кН×мОпределяем момент от собственного веса кровли и веса рабочего с инструментом при отсутствии снеговой нагрузки. Расчетная нагрузка от веса рабочего с инструментом F=1,0×1,5=1,5 кН. Постоянная нагрузка от веса кровли и собственного веса полки q’п=(1,2+25×43,2×1,35)×1,0=1459,2 M’sd= 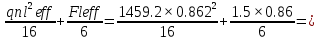 67.98 кН×м 67.98 кН×мПо наибольшему моменту M’sd подберем арматуру для полки плиты из проволоки класса S500, fyd=410 МПа. Расчет выполняем по деформационной модели. Esy= 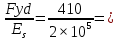 2,05 %о 2,05 %о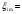 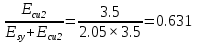 αm,lim= 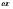 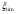 (1-K2 (1-K2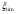 )=0.81×0.631(1-0.416×0.631)=0.377 )=0.81×0.631(1-0.416×0.631)=0.377αm= 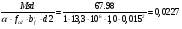 η=0.5+ 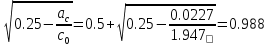 Требуемая площадь сечения арматуры на ширину 1,0 м 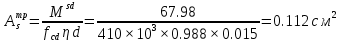 Принимаем 10Ø3, Аs=2,54 см2 ,шаг стержней 100 мм. По всей ширине полки 30 стержней, 8 6 As=2,26 см2 S240 2.1.4 Расчет поперечного ребра Поперечное ребро рассматриваем как однопролетную шарнирно опертую балку таврового сечения. Расчетная схема ребра плиты с двумя вариантами нагрузок.
Постоянной нагрузки и сосредоточенной от веса рабочего с инструментом. Расчетный пролет равен расстоянию между осями продольных ребер: leff = 2,98 – 0,1 = 2,88 м. Высота поперечного ребра h = 150 мм, толщина bw = (40 + 120)/2 = 80 мм . Толщина полки 30 f h мм. Так как 30 f h мм > 0,1h = 0,1150 = 15 мм, то расчетная ширина полки f b рав- на шагу поперечных ребер 990 f b мм. Ребро армируем одним плоским каркасом. Рабочая арматура (продольная и поперечная) из стержней класса S400. Принимаем с = 30, сcov = 20 мм), тогда d = h – c = 150 – 30 = 120 мм. Собственный вес ребра 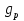 25×(0,15×0,03)×0,08×1,35=0,324 кН/м, тогда: 25×(0,15×0,03)×0,08×1,35=0,324 кН/м, тогда:– полная нагрузка 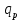 = =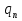 ×0,99+ ×0,99+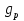 =4,95×0,99+0,324=5,22 кН/м; =4,95×0,99+0,324=5,22 кН/м; – постоянная нагрузка 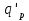 = =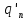 ×0,99+ ×0,99+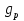 3,15×0,99+0,324= 3, 44 кН/м. 3,15×0,99+0,324= 3, 44 кН/м.Определим изгибающие моменты в пролете и поперечные силы у опор при двух вариантах загружения: 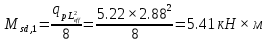 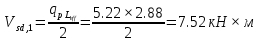 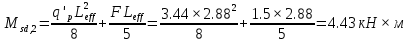 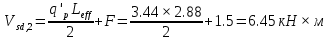 Наиболее выгодным является первый вариант загружения ребра плиты. Расчет продольной арматуры выполнения по методу предельных усилий. Проверяем условие 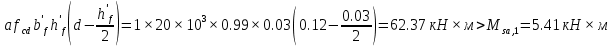 , следовательно, граница сжатой зоны проходит в полке. Сечение рассчитываем как прямоугольное с шириной b=b’f , следовательно, граница сжатой зоны проходит в полке. Сечение рассчитываем как прямоугольное с шириной b=b’f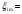 αm= αm=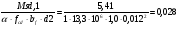 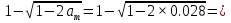 0,028 0,028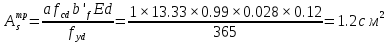 Принимаем 10Ø14 S400, Аs=1,539. Выполним расчет поперечного ребра на действие поперечной силы. Проверим условие 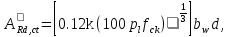 Должно быть не менее 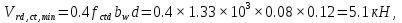 Где k=1+ 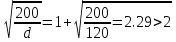 , принимаем k=2; , принимаем k=2;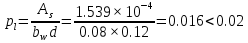 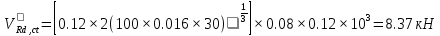 Условие 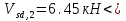 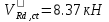 выполняется, поэтому поперечная арматура устанавливается конструктивно. Принимаем поперечную арматуру из стержней 6Ø S400 с шагом: выполняется, поэтому поперечная арматура устанавливается конструктивно. Принимаем поперечную арматуру из стержней 6Ø S400 с шагом:
2.2 Расчет продольного ребра в стадии эксплуатации 2.2.1 Определение площади сечения продольной арматуры Расчетный пролет ребра по осям опор: leff = 5,98 – 20,05 = 4,98 м. Изгибающий момент от полной рас- четной нагрузки в середине пролета. 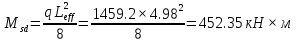 Поперечное сечение плиты приводим к тавровой форме с размерами: h = 450 мм; bw = 2100 = 200 мм; fb = 2950 мм; fh = 30 мм. Расчет ведем методом предельных усилий. Проверяем условие, опреде- ляющее положение нейтральной оси. Рабочая высота сечения d = h – c = 450 – 50 = 400 мм, 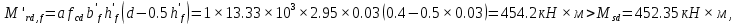 следовательно, граница сжатой зоны проходит в полке. Расчет ведем, как прямоугольного сечения с шириной b=fb=2,95 м. Граничное значение относительной высоты сжатой зоны сечения 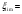 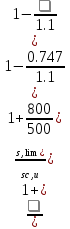 Где =kc-0.008fcd=0.85-0.008 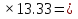 0.747, sc,u=500 МПа; 0.747, sc,u=500 МПа;s,lim=fpd+400-pm,t-pm,t=1000+400-0.6 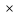 1000=800 МПа; 1000=800 МПа;pm,t – величина предварительного напряжения арматуры. При подборе арматуры, когда неизвестно напряжение pm,t , допускается ее величину принимать равной 0.6fpd pm,t= 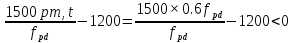 Определяем коэффициент αm= 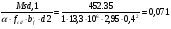 Относительная высота сжатой зоны бетона =1- 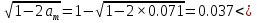 lim=0.478 lim=0.478Вычисляем значение коэффициента sn sn=-(-1) 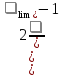 Принимаем sn= =1.15 Требуемая площадь напрягаемой арматуры 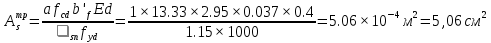 Принимаем 12Ø12 К-7, Ар= 10,87 см2 Проверяем несущую способность сечения (d=0.37 м): = 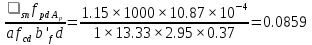 αm= 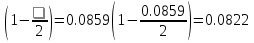 Mpd=amafcdb’d2=0.0822 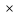 1 1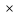 13.33 13.33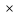 103 103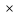 2.95 2.95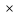 0.372=492.51 кН 0.372=492.51 кН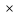 2 > Msd=452.35 2 > Msd=452.35Прочность расчетного сечения обеспечена. 2.2.2. Геометрические характеристики расчетного сечения Сечение ребристой панели приводим к эквивалентному (по площади и моменту инерции) тавровому сечению. Площадь поперечного сечения плиты Ас=hbw+h’f(b’f-bw)=0.45 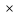 0.2 0.2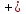 0.03(2.95-0.2)=0.1725 м2 0.03(2.95-0.2)=0.1725 м2Определяем положение центра тяжести бетонного сечения: - статический момент относительно нижней грани бетонного сечения Sc= 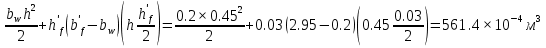 - расстояние от нижней грани до центра тяжести бетонного сечения yc= 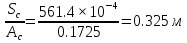 Момент инерции бетонного сечения Ic= 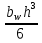 + +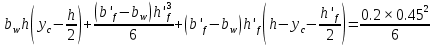 + +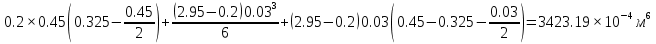 Площадь напрягаемой арматуры Ap=10.87 cм2. Коэффициент ap= 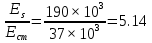 Определяем положение центра тяжести приведенного сечения: - площадь приведенного сечения Ared=Ac+apAp=0.1725+5.14 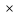 10.87 10.87 10-4=0.178 м2 10-4=0.178 м2- статический момент приведенного сечения относительно нижней грани сечения lim , lim , 0,690 0,432, 800 0,690 1 1 1 1 1,1 500 1,1 s sc u где 0,008 0,85 0,008 20 0,690; c cd k f , 500 sc u МПа; , lim , , 400 1000 400 0,6 1000 800 s pd pm t pm t f МПа, pm t, – величина предварительного напряжения арматуры. При подборе арматуры, когда неизвестно напряжение , , pm t допускается ее величину принимать равной 0,6fpd. Величина , , 1500 1500 0,6 1200 1200 0. pm t pd pm t pd pd f f f Определяем коэффициент ,1 2 32 324, 4 0,0344. 1 20 10 2,95 0, 4 Sd m cd f M f bd Относительная высота сжатой зоны бетона 1 1 2 1 1 2 0,0344 0,035 0, 432. m lim 33 Вычисляем значение коэффициента sn (пункт 9.1.4 [1]): lim 0,035 1 2 1 1,15 1,15 1 2 1 1,28 1,15, 0,432 sn принимаем 1,15. sn Требуемая площадь напрягаемой арматуры тр 1 20 2,95 0,035 0, 4 4 7,18 10 1,15 1000 cd f s sn pd fb d A f м2 = 7,18 см2 . Принимаем 1212 К–7, Аp = 10,87 см2 . Рисунок 2.4 – Схема расположения напрягаемой арматуры в продольном ребре Схема расположения напрягаемой арматуры приведена на рисунке 2.4. Проверяем несущую способность сечения (d = 0,37 м): 4 1,15 1000 10,87 10 0,0573 1 20 2,95 0,37 sn pd p cd f f A f bd ; 0,0573 1 0,0573 1 0,0557; 2 2 m 2 32 0,0557 1 20 10 2,95 0,37 M f bd pd m cd = 449,9кНм > MSd = 324,4 кНм. Прочность расчетного сечения обеспечена. На 1м длины плиты шириной 300 см действуют следующие нагрузки: Кратковременная нормативная: рn=800×3,0=2400,0 Н/м кратковременная расчетная р=1200×3,0=3600,0 Н/м постоянная и длительная нормативная qn=2934×3,0=8802,0 Н/м постоянная и длительная расчетная q=3961,5×3,0=11884,5 Н/м итого расчетная q+ р=11884,5+3600=15484,5 Н/м итого нормативная qn+ рn=8802,0+2400=11202,0 Н/м расчетный изгибающий момент от полной нагрузки М=ql02/8=15484,5×6,02/8=22226,8 Н×м расчетный изгибающий момент от полной нормативной нагрузки Мn=qnl02/8=11202,0×6,02/8=16803,0 Н×м нормативная постоянная и длительная временная нагрузка Мld=8802,0×6,02/8=13203,0 Н×м максимальная поперечная сила на опоре от расчетной нагрузки Vsd=ql0/2=15484,5×6,0/2=46453,5Н=46,5 кН 2.1.3 Расчет по прочности нормальных сечений Плиту рассчитываем как балку прямоугольного сечения с заданными размерами bxh=300×30см (где b-минимальная ширина; h-высота панели). Расчетная ширина сжатой полки bn’ =146 см. Отношение h’f/h=3.85/30=0.175>0.1; в расчет вводим всю ширину полки b’ʄ=146см. Вычисляем по формуле: αm= 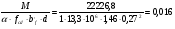 где d=h-c=30-3=27см, fcd=fck/γc=20/1.5=13.3 МПа По таблице 2.12 [2] находим ξ=0,058, =0,971. Площадь сечения продольной арматуры As= 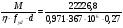 =2,31 см2 =2,31 см2предварительно принимаем 2Ø18, Аs=2,54 см2, а также учитываем сетку из проволоки 8 6 As=2,26 см2 S240 (шаг 200); As=2,54+2,26=4,8 см2 2.1.4 Расчет по прочности наклонных сечений Вычисляем проекцию с наклонного сечения по формуле: linc= ηc2(1+ηf+ηN) ×fctd×b×d2/(Vsd×0,5) где ηc2=2-для тяжелого бетона; ηf=8×0.75× 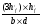 = 8×0.75× = 8×0.75×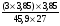 = 0,21<0.5 = 0,21<0.5link=2(1+0,21) ×1.0×106×0,459×0.272/(46453,5×0,5)= 4,78>2×d=0,54 fctd= 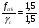 =1МПа =1МПаПринимаем link=0,54м Vrd=46453,5/0.54=86025,0 H>Vsd=46453,5H Поперечная арматура по расчету не требуется. Назначаем арматуру 6 S240 шагом 10см у опор на участках длиной ¼ пролета, в средней части панели для связи продольных стержней каркаса по конструктивным соображениям ставим поперечные стержни через 50 см. 2.1.5 Расчет прогибов Определим прогиб панели приближенным методом, используя значения ƛlim. Для этого предварительно вычислим: 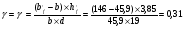 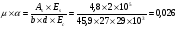 Прогиб в середине пролета панели от постоянных и длительных нагрузок вычисляется по формуле: 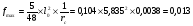 м мгде 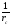 – кривизна в середине пролета панели, определяется по формуле: – кривизна в середине пролета панели, определяется по формуле: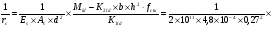 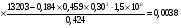 где коэффициенты k1ld = 0,424 и k2ld = 0,184 приняты по таблице в зависимости от µα = 0,067 и 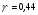 для двутавровых сечений. для двутавровых сечений.2.1.6 Определение ширины раскрытия трещины Ширина раскрытия трещин определяем по формуле: arc= δ×φl×η×20× (3.5-100μ) × 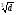 × δа × δаδ=1-как для изгибаемых элементов, η=1-для стержневой арматуры периодического профиля, d=19 cм - по расчету, Es=2×105 МПа - для стали, δа =1, μ= 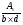 =4,8/(45,9×27)=0,003 =4,8/(45,9×27)=0,003φc=1,6-1,5μ=1,6-1,5×0,003=1,59 Здесь =0,55; 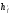 /d=3,85/27=0,14; d=27, по формуле находим ξ /d=3,85/27=0,14; d=27, по формуле находим ξξ= 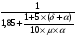 λ=[1-/2d]=0,55[1-3,85/(2×27)]=0,028; Значение δ от действия от всей нормативной нагрузки: δld= 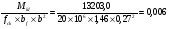 ξ= 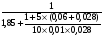 =0,0019<0,2 =0,0019<0,2Продолжаем расчет как прямоугольного сечения z1=d(1-0.5×ξ)=27×(1-0,5×0,0019)=26.97 см Упругопластический момент сопротивления ж/б таврового сечения после образования трещин Ws=AsZ1=4,8×26,97=129,45 см3; Напряжение в растянутой арматуре при действие постоянных нагрузок: σs2=Mld/Ws=13203/129,45=102,0 МПа Ширина раскрытия трещины от действия постоянной нагрузки aarc2=1×1.45×1× 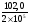 ×20× (3.5-100×0.010)× ×20× (3.5-100×0.010)×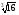 ×1=0,251 мм ×1=0,251 мм arcmax=0.3мм; условие удовлетворяется. Расчет по кратковременному раскрытию трещин. Напряжение в растянутой арматуре при совместном действии всех нормативных нагрузок: σs1=Mn/Ws=16803/129,45×10-6=129,8 МПа Δσs=σs1- σs2=129,8-102,0=27,8 МПа Соответствующие приращение ширины раскрытия трещин при φ1=1 будет: Δaarc1-aarc2=1×1×1× 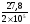 ×20(3.5-100×0.010)× ×20(3.5-100×0.010)×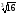 ×1=0.047 мм ×1=0.047 ммШирина раскрытия трещин при совместном действии всех нагрузок aarc=0,047+0,251=0,298 < acrc1,max=0.4мм т.е. условие удовлетворяется. 2.1.7 Расчет плиты на монтажные нагрузки С учетом коэффициента динамичности kd=1.4 расчетная нагрузка от собственного веса панели: q=kdγfgb=1.4×3713×1.49=7745.3H/м; Отрицательный изгибающий момент консольной части панели М=q/2=7745.3×0.72/2=1897.6H×м Пологая, что Z1=0.9d, требуемая площадь сечения указанной арматуры составляет: As=M/(Z1×fyd)=1897.6/(0.9×0.19×365×106)=0.3см2 что значительно меньше принятой арматуры 410 As=3.14см2 Усилие на одну петлю составляет: N=ql/2=7745.3×5,98/2=23158,45 H Площадь сечения арматуры петли: As=N/fyd=23158,45/218×106=1,06 см2 Принимаем конструктивно стержни 12мм класса S240; As=1.13см |
