2. Сформулировать 1 и 2 зак Кирхгофа iый закон
 Скачать 242.63 Kb. Скачать 242.63 Kb.
|
|
1. Записать компонентные уравнения элементарных двухполюсников по временной форме А) резистор 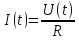 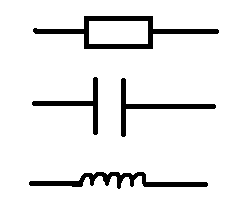 Б) конденсатор 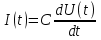 В) катушка 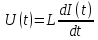 (катушка определяется через ток, конденсатор через напряжение) 2. Сформулировать 1 и 2 зак Кирхгофа I-ый закон Алгебраическая сумма токов в узле равна нулю 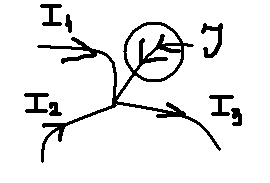 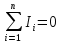 «i» - номер ветви «n» - число ветвей подключенных к узлу «+» - если ток вЫтекает «-» - если ток втекает 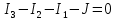 II-ой закон Алгебраическая сумма напряжений, при обходе по контуру цепи, равна нулю 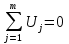 «j» - номер ветви «m» - число ветвей в контуре «+» - если направление напряж в ветви совпадает с направлением обхода «-» - если направление напряж в ветви НЕ совпадает с направлением обхода 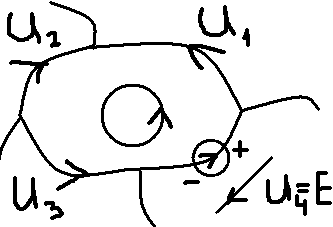 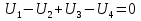 Перефразируем Алгебраическая сумма напряжений на пассивных ветвях равна алг сумме ЭДС источников 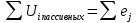 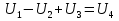 3. Сформулировать теорему Тевенина. Привести пример Произвольный линейный двухполюсник, содержащий (кроме пассивных элементов), источник тока и (или) напряжения, может быть эквивалентно заменен двухполюсником состоящим из послед соед идеальным ист ЭДС(Еэг) и сопротивлением(Rэг). ЭДС(Еэг)= напряжению холостого хода на зажимах исходного двухполюсника, а сопротивление(Rэг)= сопротивлению исходного двухполюсника при отключенных источниках(источники ЭДС закорачиваются (Ei=0) источники тока обрываются(Ji=0)) 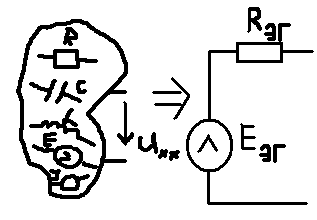 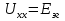 4. Сформулировать теорему Нортона. Привести пример Произвольный линейный двухполюсник, содержащий (кроме пассивных элементов), источник тока и (или) напряжения, может быть эквивалентно заменен двухполюсником состоящим из параллельно соед идеальным ист тока(Jэг) и проводимостью(Yэг). Ток(Jэг) = току короткого замыкания на зажимах исходного двухполюсника, а проводимость(Yэг).= проводимости исходного двухполюсника при отключенных источниках(источники ЭДС закорачиваются (Ei=0) источники тока обрываются(Ji=0)) 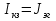 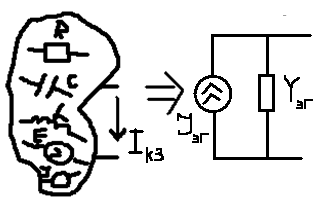 5. Привести пример записи ур цепи по методу контурных токов 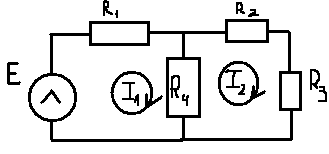 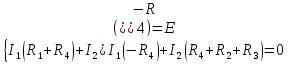 6. Привести пример записи ур цепи по методу узловых потенциалов 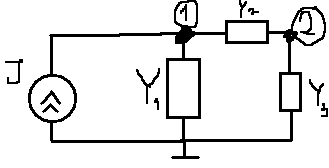 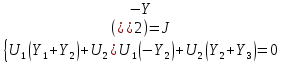 7. Дать опр комплексной амплитуды гармонич колебания 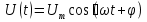 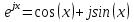 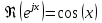 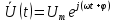 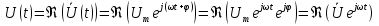 Где 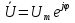 8. Дать опр комплексного сопротивления двухполюсника 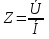 полноесопротивление(импеданс) полноесопротивление(импеданс)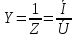 полная проводимость полная проводимостьZ=R+jX Y=G+jB R,G – активное(ая) сопротивление/проводимость X,B - реактивное(ая) сопротивление/проводимость 9. Записать выражения для комплексных сопротивлений Элементарных двухполюсников А) резистор 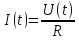 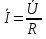  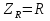 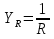 Б) конденсатор 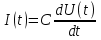 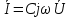 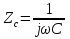 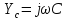 В) катушка 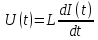 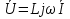 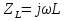 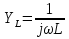 10. Записать компонентные уравнения элементарных двухполюсников в комплексной форме 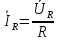 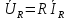 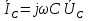 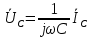 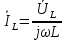 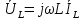 11. Дать определение комплексной мощности Пусть есть   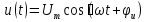 обозначим 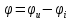 тогда 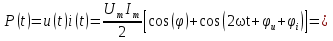 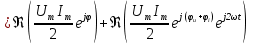 Пояснение для будущего 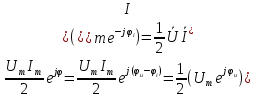 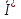 - это комплексно сопряженный ток - это комплексно сопряженный токТогда 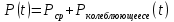 Где 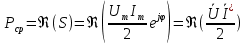 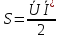 S– комплексная мощность(не зависит от t), а Pколеб зависит S– комплексная мощность(не зависит от t), а Pколеб зависит12. Дать определение средней мощности P(t)=Pcp+Pколеб(t), Рср это та величина относительно которой колеблится мощность(вывод такой же как и в пункте 11, только S тут не причем)(вообще про мощность можно сказать, что если P(t)<0, то система отдает энергию, если Р(t)>0 тогда получает энергию)(на графике на цифры не смотреть, только на буквы смотреть) 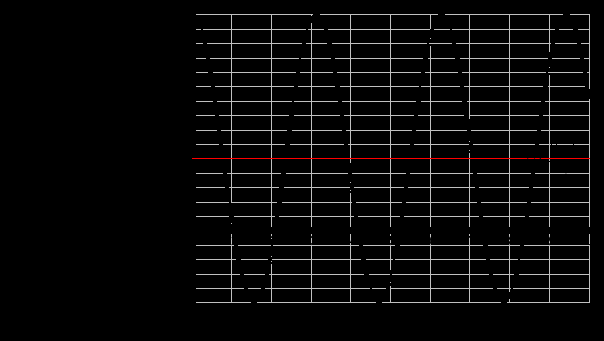 13. Дать определение активной мощности S=P+jQ P – активная мощность 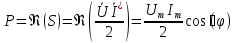 [Вт]=[Ватт] [Вт]=[Ватт]14. Дать определение реактивной мощности S=P+jQ Q – реактивная мощность 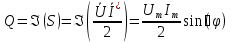 [ВАР]=[Вольт Ампер Реактивный] [ВАР]=[Вольт Ампер Реактивный]15. Дать определение полной мощности S=P+jQ |S| – полная мощность мощность 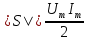 [ВА]=[Вольт Ампер] [ВА]=[Вольт Ампер]16. Сформулировать условие передачи максимальной средней мощности от источника в нагрузку 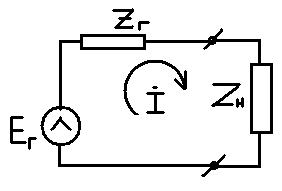 Zг=Rг+jХг Zн=Rн+jХн 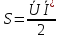 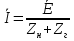 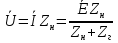 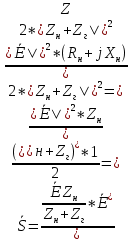 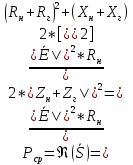 Надо потребовать чтобы Xн=-Хг (1) 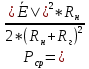 Надо чтобы 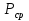 было max, значит было max, значит 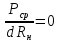 мы получим что Rн=Rг (2) мы получим что Rн=Rг (2)Из (1) и (2) поучаем, что 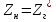 сопр нагрузки должно быть равно комп сопряж сопр генератора. сопр нагрузки должно быть равно комп сопряж сопр генератора.17. Дать опр комплексной передаточной функции 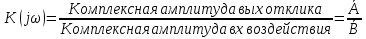 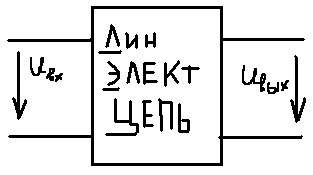 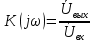 Коэф передачи по напряжению 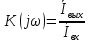 Коэф передачи по току 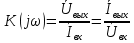 Коэф передачи «смешанный» 18. Дать опр АЧХ цепи 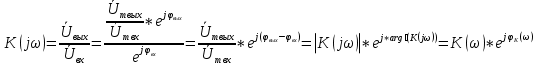 K(  ) – Амплитудно-Частотная Характеристика(мы много таких видели) ) – Амплитудно-Частотная Характеристика(мы много таких видели)19. Дать опр ФЧХ цепи 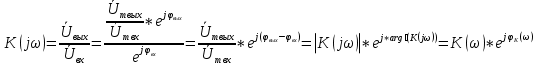  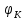 ( (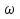 ) – Фазо-Частотная Характеристика(мы много таких видели) ) – Фазо-Частотная Характеристика(мы много таких видели)Но, на всякий случай:
20. Изобразить последовательный колебательный контур 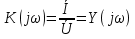 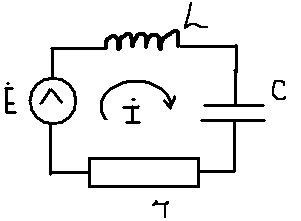 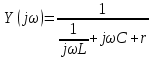 Анализ этих 2ух строчек занимает много страниц, да и не требуется это в данном вопросе(Снимаем с кондера) 21. Изобразить параллельный колебательный контур 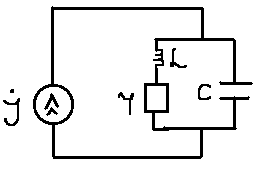 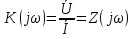 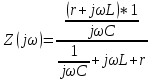 Анализ этих 2ух строчек занимает много страниц, да и не требуется это в данном вопросе 22. Дать опр резонансной частоты в колебательном контуре Резонансная частота это частота на которой реактивное сопротивление частоты становится равным нулю. Резонанс – резкое возрастание(из-за предыдущего предложения) амплитуды тока или напряжения Если привести 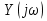 к виду к виду 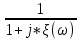 , то , то 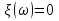 (обобщенная расстройка)когда (обобщенная расстройка)когда 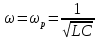 , у параллельного как то получается так же. , у параллельного как то получается так же.Резонанс у паралллельного это резонанс токов, т.е. 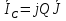 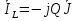 У последовательного есть анологичная штука(но почему то ее не назвали «резонансом напряжения») 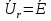 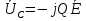 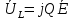 23. Дать опр характерестического сопротивления колеб контура Характерестическое сопротивление - это сопротивления на реактивных ветвях при 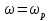 На конденсаторе 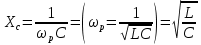 На катущке 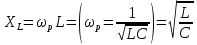 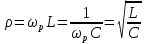 24. Дать опр добротности колеб контура Послед колеб контур Надо вернуться к 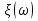 (обобщенная расстройка), если привести (обобщенная расстройка), если привести 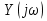 к виду к виду 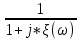 , ,То 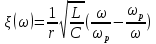 , где , где 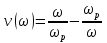 относительная расстройка относительная расстройкаТо безразмерный коэффициент перед 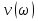 есть добротность есть добротность 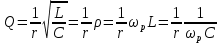 Парралельн колеб контур Надо привести 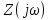 к виду к виду 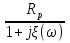 Где 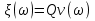 Но 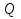 теперь равно теперь равно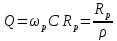 Характеризует качество контура. Чем больще тем лучше. 25. Дать опр резонансного сопротивления Это получаем из параллельного контура. Надо привести 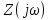 к виду к виду 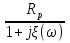 (В Баскакове (В Баскакове  ) ) Сопротивление цепи на резонансной частоте(Потому как на резонансной частоте реактивное сопротивление равно нулю) 26. Дать опр полосы пропускания контура При   Из-за того приближения   Можно сказать что  Потому  «Действительное значение» Y(j  ) это ) это 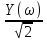 , в этих точках , в этих точках 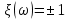 Решаем уравнение 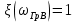 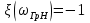    Полоса пропускания(  - граничная частота нижняя(верхняя)) - граничная частота нижняя(верхняя))27. Изобразить АЧХ 2ух высокодобротных связанных колеб контуров при факторе связи А<1, A=1,A>1 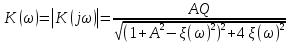 , тут взято за переменную 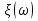 , при переходе обратно на зависимость только от , при переходе обратно на зависимость только от 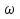 , мы получим теже картинки только сдвинутые по оси Х, т.е. х=0 станет , мы получим теже картинки только сдвинутые по оси Х, т.е. х=0 станет 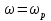 . Можно обратить внимание на «тупой нос» у К(х,1), это значит, то что мы(человечество) хотим(стремимся) получить фильтр с прямоугольным АЧХ. . Можно обратить внимание на «тупой нос» у К(х,1), это значит, то что мы(человечество) хотим(стремимся) получить фильтр с прямоугольным АЧХ.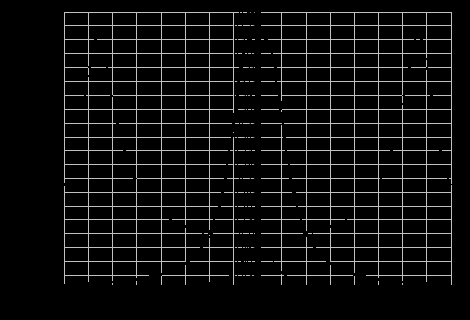 A<1 слабая связь(0,1 на рис) А=1 критическая связь(1 на рис) A>1 сильная связь(10 на рис) 28,30. Записать уравнения системы Z-параметров линейного 4ехполюсника 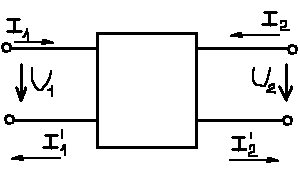   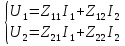 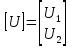 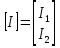 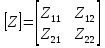 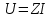 матричная запись ур-ний сис Z-параметров матричная запись ур-ний сис Z-параметров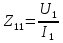 при при 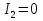 - входное сопротивление 4ех полюсника в режиме хх на выходе - входное сопротивление 4ех полюсника в режиме хх на выходе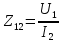 при при 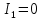 - взаиное сопротивление обратной передачи в режиме хх на входе - взаиное сопротивление обратной передачи в режиме хх на входе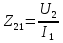 при при 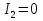 - взаиное сопротивление прямой передачи в режиме хх на выходе - взаиное сопротивление прямой передачи в режиме хх на выходе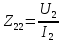 при при  - выходное сопротивление 4ех полюсника в режиме хх на входе - выходное сопротивление 4ех полюсника в режиме хх на входе29. Записать уравнения системы Y-параметров линейного 4ехполюсника    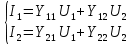 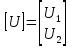 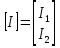 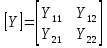 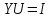 матричная запись ур-ний сис Y-параметров матричная запись ур-ний сис Y-параметров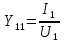 при при 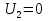 - входная проводимость 4ех полюсника в режиме к/з на выходе - входная проводимость 4ех полюсника в режиме к/з на выходе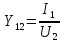 при при 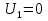 - взаиная проводимость обратной передачи в режиме к/з на входе - взаиная проводимость обратной передачи в режиме к/з на входе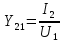 при при 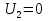 - взаиная проводимость прямой передачи в режиме к/з на выходе - взаиная проводимость прямой передачи в режиме к/з на выходе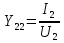 при при 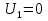 - выходная проводимость 4ех полюсника в режиме к/з на входе - выходная проводимость 4ех полюсника в режиме к/з на входе31. Дать опр линейного трансформатора Трансформатор – устройство для передачи эл.маг. энергии из одной части в другую, используя принцип магнитной связи. 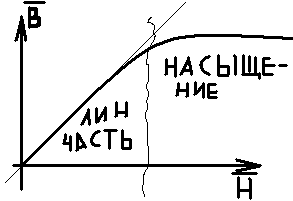 Как я понял сколько получил, столько отдал(не усиливает и не уменьшает ничего) 32. Дать опр ВАХ НЭ ВАХ НЭ – это функциональная(нелинейная) зависимость тока от напряжения 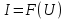 33. Дать опр нагрузочной прямой Прямая с параметрами цепи, с помощью которой можно опр напряжение или ток НЭ 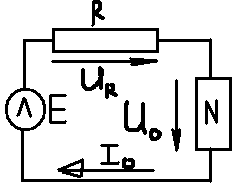 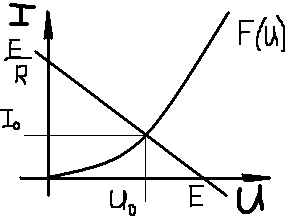 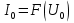 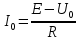 Прямая эта 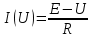 34. Дать опр основной(первой гармоники), высшие гармоники тока 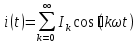 при k=0 – постоянная составляющая(сos(0)=1 => I0) k=1 – первая гармоника(основная) (сos(  ) => I1 сos( ) => I1 сos( )) ))k>1 – высшие гармоники чем больще k тем меньше Ik……наверно 35. Дать опр переходного процесса Это процесс перехода из одного установившегося состояния в другое. 36. Дать опр коммутации Это любое скачкообразное изменение в цепи 37. Дать опр функции Хевисайда Это испытательный сигнал 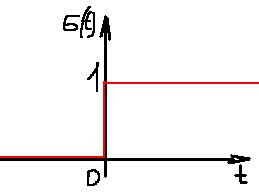 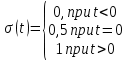 38. Дать опр функции Дирака Это испытательный сигнал 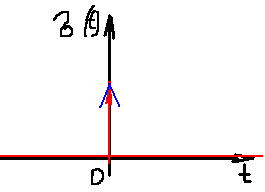 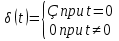 39. Дать опр переходной характеристики лин цепи g(t) это переходная характеристика, если является выходным откликом на входное воздействие 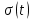  40. Дать опр импульсной характеристики лин цепи h(t) это импульсная характеристика, если является выходным откликом на входное воздействие 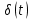 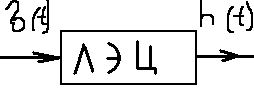 41. Дать опр свободного процесса в лин цепи Свободный процесс(колебание) это процесс который вызван из-за запаса энергии.(Конденсатор не разрядился(да и он в прицнипе никогда не разряжается, только стремится к нулю))   (Или при решении дифура мы решаем однородное уравнение) 42. Дать опр вынужденного процесса в лин цепи Вынужденный процесс(колебание) это процесс который вызван из-за внешнего воздействия на цепь  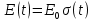 (Или при решении дифура мы решаем НЕоднородное уравнение) 43. Изобразить схему интегрирующей RC-цепи    Чтобы цепь интегрировала надо что бы 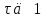 т.е. т.е.При сумме можно было пренебречь единицей и получить 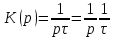 Где 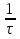 это какой то коэффициент, а это какой то коэффициент, а 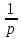 эквивалентно интегралу, т.к эквивалентно интегралу, т.к  44. Изобразить схему дифференцирующей RC-цепи    Чтобы цепь дифференцировала надо что бы 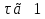 т.е. т.е.При сумме можно было пренебречь 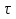 и получить и получить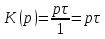 Где 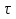 это какой то коэффициент, а это какой то коэффициент, а 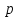 эквивалентно дифференциалу, т.к эквивалентно дифференциалу, т.к 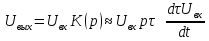 45. Сво-ва преобразования Лапласа: формулировка теор интегрирования Интеграл оригинала подобен делению изображению деленное на p 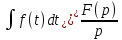 46. Сво-ва преобразования Лапласа: формулировка теор о свертке Пусть 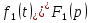  Тогда  47. Сво-ва преобразования Лапласа: формулировка теор запаздывания Пусть  Тогда  48. Дать опр операторного сопротивления двухполюсника 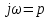   операторное сопр операторное сопр операторная проводимость операторная проводимость49. Дать опр операторной передаточной функции   Становится  Где  - операторная передаточная функция - операторная передаточная функция50. Записать компонентные уравнения элементарных двухполюсников в операторной форме А) резистор 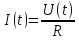 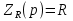 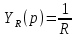 Б) конденсатор 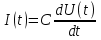   В) катушка   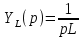 51. Привести примерпоиска изображения по Лапласу при заданном оригинале Можно находить по определению  Можно находить по таблице. Пример (a – какая то константа)Пусть  По таблице  По определению сложно, не делаем  52. Записать интеграл Дюамеля, пояснить расстановку пределов Подготовка   Пусть  тогда тогда   , при этом, т.к. , при этом, т.к. , значит , значит по опр импульсной хар-ки по опр импульсной хар-ки значит  , где , где   Интеграл Дюамеля(интеграл супперпозиции, свертка)  Если 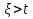 тогда тогда 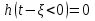 (импульсная хар-ка равна нулю(там нет сигнала, нечего характеризовать)) (импульсная хар-ка равна нулю(там нет сигнала, нечего характеризовать))Если 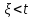 тогда тогда 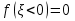 в отрицательной области нет сиганала(не включен еще) в отрицательной области нет сиганала(не включен еще)53. Понятие о линии передач Линия передачи – система, предназначенная для соединения источника сигнала и приемника, разнесенных в про-ве(не обязательно большом, главное  ) )  - длина линии, - длина линии,  – длина волны. – длина волны.   - длина волны 3см, возьмем цепь длиной в 1м(100см) уже можно говорить о линии передач - длина волны 3см, возьмем цепь длиной в 1м(100см) уже можно говорить о линии передач54. Как вводятся погонные параметры линии передачи Т.к. линии передачи может быть разнесена на большие расстояния то легче дать параметры  , т.е. погонные. Что бы узнать обычные параметры линии, надо будет домножить на длину линии. , т.е. погонные. Что бы узнать обычные параметры линии, надо будет домножить на длину линии.   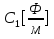 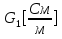  55. Что такое волны Даламбера Положения точек равных фаз определяется уравнением   56. Записать выражения для прямой(обратной) волны напряжения в беск протяженной лини передачи при гармоническом возбуждении.   - коэффициент распространения - коэффициент распространения – коэффициент затухания – коэффициент затухания – коэффициент фазы – коэффициент фазыГармонические возбуждения = комплексные амплитуды   57. Дать опр волнового сопр линии передач «пр» - прямое(ой) «обр» - обратное(ый)   Подставляем в систему  Получаем  Значит  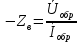 Связь между током и напряжение в линии, если есть мнимая часть то можно говорить о сдвиге между U и I 58. Дать опр длины волны в линии передач Пространственный период волны 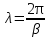 59. Дать опр фазовой скорости в линии передач Скорость перемещения плоскости равных фаз Ур плоскости 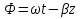 , гдн Ф=const , гдн Ф=const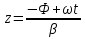  60. Что такое падающая и отраженная волна  – та волна, которая распространяется от источника к нагрузке – та волна, которая распространяется от источника к нагрузке – та волна, которая распространяется от нагрузки к источнику – та волна, которая распространяется от нагрузки к источнику 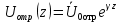 61. Дать опр коэф отражения Какая часть энергии отразится, а какая поглотится нагрузкой 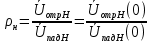 62. Дать опр КБВ  63. Дать опр КСВ  64.Записать коэф отр от нагрузки в линии без потерь сзаданным Zв и Zн   65.Что такое согласованный режим Это когда Zн=Zв, т.е. коэф отражения равен нулю, тоесть вся энергия уходит в нагрузку 66.Изобразить распределении амплитуды при к/з       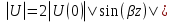 67.Изобразить распределении амплитуды при обрыве цепи  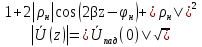 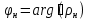     68. Дайте опр ф-ии сопротивления(пров) лин 2ухполюсника (Проводимость 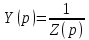 ) )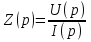 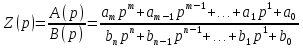  - не отрицательные чисто вещественные - не отрицательные чисто вещественныеПриводим к виду  69,70. «Нули» и «полюсы» ф-ии сопр(пров) Нули Z(p) это {  }, там где Z(p)=0 }, там где Z(p)=0Полюсы Z(p) это {  }, там где Z(p) не существует }, там где Z(p) не существует71.Изобразите карту нулей и полюсов функции сопротивления параллельного колеб контура   Нуль(Кружочек)   Полюсы(крестики)  пусть  тоогда тоогда , где , где  72. Изобразите канонические схемы для синтеза двухполюсников по Фостеру  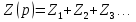 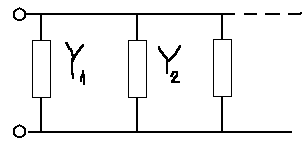 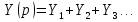 73. Изобразите канонические схемы для синтеза двухполюсников по Кауэру 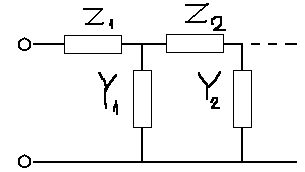    74,77,78. Что такое фильтр Баттерворта  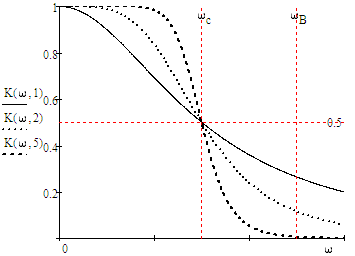 75,78. Что такое фильтр Чебышева 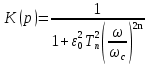 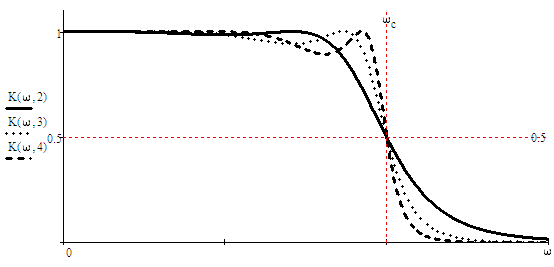 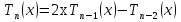 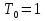 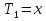 76. Что такое фильтр-прототип Это ФНЧ, после подстановки в него параметров, мы можем получить ФВЧ или ПФ 79. Физическая реализуемость Все особые точки должныбыть в левой полу-плоскости. |
