рк1. 2. слабонаправленное излучение симметричных вибраторов краткая теория симметричного вибратора
 Скачать 1.59 Mb. Скачать 1.59 Mb.
|
|
3. ОСТРОНАПРАВЛЕННОЕ ИЗЛУЧЕНИЕ АНТЕННЫХ РЕШЕТОК 3.1. Формирование остронаправленного излучения с помощью антенных решеток Формирование узких ДН является очень важной и актуальной задачей для современных беспроводных систем телекоммуникаций. Антенны с такими ДН широко используются в спутниковых системах телекоммуникаций, радионавигации, радиопеленгации, радиолокации, мобильной и радиорелейной связи. Под узкой ДН подразумевается наличие в ней одного (или двух, реже более двух) главного лепестка, имеющего очень малую ширину. Это означает, что антенна обладает остронаправленным излучением (или приемом), т.е. она имеет высокие направленные свойства, или высокое значение КУ. Направленная антенна концентрирует энергию электромагнитного поля в пространство в виде узкого пучка, при этом излучение в других направлениях необходимо свести к минимуму. Наиболее типичные остронаправленные ДН показаны на рис.3.1. Существуют различные виды направленных антенн, одними из которых являются антенные решетки (АР). АР в общем случае представляет собой систему элементов, расположенных определенным образом в пространстве и возбужденных высокочастотными токами с определенными амплитудами и фазами. В зависимости от расположения элементов различают линейные, плоские, кольцевые, цилиндрические и другие АР (рис.3.2). В качестве элементов в АР чаще всего используются слабонаправленные излучатели: вибраторы, щели, открытые концы волноводов и др. В некоторых беспроводных системах телекоммуникаций эксплуатируются АР, в качестве элементов которых используются направленные излучатели: спирали, антенны типа «волновой канал», рупоры и др. Принцип работы АР основан на синфазном сложении электромагнитных полей, создаваемых отдельными элементами решетки, в определенном (главном) направлении, в результате чего происходит увеличение напряженности поля в этом направлении за счет ее уменьшения в других направлениях. Однако это происходит при условии, что сдвиг фаз полей от отдельных излучающих элементов в точке наблюдения из-за несинфазности возбуждения компенсировался бы сдвигом фаз, возникающим из-за разности расстояний, проходящих волнами от каждого элемента до точки наблюдения. Сказанное справедливо, если расстояние между соседними элементами настолько велико, что их взаимным влиянием можно пренебречь.     Рис.3.1 Виды остронаправленных диаграмм направленности  Рис.3.2 Виды антенных решеток По способу возбуждения элементов АР делят на: – синфазные; – несинфазные (фазированные); – равноамплитудные; – неравноамплитудные. По виду расположения элементов АР делят на: – эквидистантные; – неэквидистантные. Синфазной называется АР, элементы которой возбуждаются токами с одинаковой фазой. Несинфазной называется АР, элементы которой возбуждаются токами с разными фазами. При этом фазовый сдвиг от элемента к элементу может иметь либо постоянное значение, либо фазы токов имеют разные значения. Равноамплитудной называется АР, элементы которой возбуждаются токами с одинаковыми амплитудами. Неравноамплитудной называется АР, элементы которой возбуждаются токами с разными амплитудами. Эквидистантной называется АР, элементы которой расположены на одинаковом расстоянии друг от друга. Неэквидистантной называется АР, элементы которой расположены на разных расстояниях друг от друга. 3.2. Линейные антенные решетки поперечного излучения Линейной АР называется система идентичных элементов, центры излучения которых расположены на прямой, называемой осью решетки. Рассмотрим направленные свойства синфазной, равноамплитудной, эквидистантной АР (рис.3.3), состоящей из n-числа слабонаправленных излучателей.  Рис.3.3 Линейная, синфазная, равноамплитудная, эквидистантная антенная решетка Такая решетка имеет ХН, определяемую выражением f(θ,φ) = f1(θ,φ) fc(θ,φ), (3.1) где f1(θ,φ) –ХН одного элемента; fc(θ,φ) – множитель системы. Выражение (3.1) носит название теоремы перемножения и показывает, что ХН АР, состоящей из идентичных элементов, представляет собой произведение ХН одного элемента решетки на множитель системы. Множитель системы не зависит от типа элементов, он зависит от количества элементов, межэлементного расстояния и рабочей длины волны. В случае если в качестве элементов используются СВ, ХН АР имеет вид: – в меридиональной плоскости 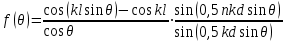 , (3.2) – в экваториальной плоскости 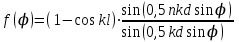 , (3.3) где n–количествоэлементов; d – межэлементное расстояние; l–длина плеча вибратора k – волновое число (2π/λ). При большом количестве вибраторов множитель системы при изменении угла θ изменяется значительно быстрее, чем множитель fc(θ). Это объясняется тем, что величина nkd/2 значительно больше величины kl. Поэтому ХН решетки, в основном, определяется множителем системы. Поскольку множитель системы является периодической функцией, то при изменении угла θ этот множитель может обращаться в нуль, затем он возрастает, достигая максимального значения, далее уменьшается, снова становится равным нулю и т.д. Из этого следует, что ДН решетки в меридиональной плоскости имеет многолепестковый характер. Напряженность излучаемого АР поля максимальна в направлениях θ=0° иθ=180°, т.е. два главных максимума ДН направлены перпендикулярно оси решетки. Поэтому такая решетка называется АР поперечного излучения. Каждый вибратор в этом направлении излучает с максимальной интенсивностью при его относительно длине, равной l/λ=0,625. Поля от отдельных вибраторов в направлении θ=0°складываются арифметически, поскольку они синфазны. При θ=0° иθ=180° выражение для множителя системы представляет собой неопределенность вида 0/0, при раскрытии которой по правилу Лопиталя оказывается, что множитель системы максимален и равен n, т.е. количеству вибраторов в решетке. Важное замечание: поскольку СВ не обладают направленными свойствами в экваториальной плоскости, то и АР в этой плоскости также не обладает направленными свойствами, т.е. ДН АР в этой плоскости имеет вид окружности. Это замечание касается только случая линейной АР. На рис.3.4 показано несколько ДН линейных АР для некоторых значений n и d/λ. Из рисунков видно, что увеличение числа элементов в АР (т.е. увеличение размера решетки) приводит к сужению главного лепестка ДН и к увеличению числа боковых лепестков. Увеличение межэлементного расстояния также приводит к сужению главного лепестка ДН, однако это происходит до значений d/λ<1. Дальнейшее увеличение межэлементного расстояния приводит к возникновению в ДН дополнительных максимумов, по уровню сравнимых с уровнем главного лепестка, таким образом, АР теряет однонаправленность излучения. Направления, в которых отсутствует излучение АР, называют минимумами (нулями) ДН. Они находятся из условия равенства нулю числителя множителя системы, т.е. (0,5nkd)sinθ0=N, откуда sinθ0 = Nλ/(nd), где N = 1,2,3, ... . Таким образом, нули ДН определяются по формуле 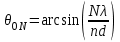 . (3.4) Направления максимумов боковых лепестков можно приближенно найти из условия максимума числителя множителя системы, так как знаменатель этого множителя при kd<<nkd (т.е. при большом числе вибраторов) с изменением угла θ изменяется значительно медленнее числителя. Это условие записывается в виде sin[(nkd/2)sinθmax] = ±1, откуда (nkd/2)sinθmax = (2N+l) 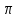 /2, где N=1,2,3,... . /2, где N=1,2,3,... .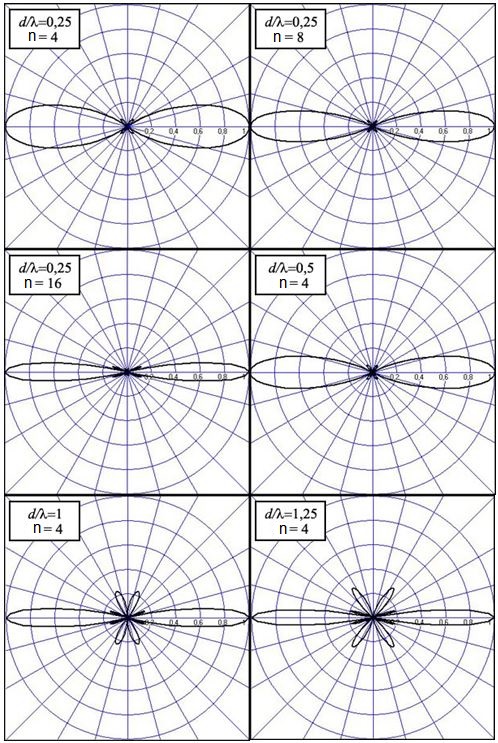 Рис.3.4 Диаграммы направленности антенных решеток Таким образом, направления максимумов боковых лепестков ДН определяются по формуле 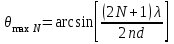 . (3.5) Ширину главного лепестка по уровню нулевого излучения определяют по формуле 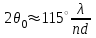 , (3.6) а его ширину по половинной мощности излучения по формуле 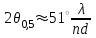 . (3.7) Уровни боковых лепестков определяют по формуле (N– номер лепестка) 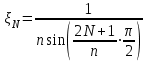 . (3.8) Уровень первого бокового лепестка ДН АР приблизительно равен 2,14 (-13,3 дБ). Уровень второго лепестка ДН АР равен 0,13. При введении фазового сдвига ψ между токами в соседних элементах АР ее ХН в меридиональной плоскости имеет вид 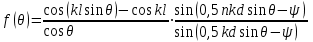 . (3.9) В результате этого главный лепесток ДН отклоняется от нормали к АР на угол, определяемый как 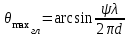 . (3.10) Таким образом, линейный закон изменения фазы токов возбуждения элементов АР приводит к изменению направления ее максимального излучения. Главный лепесток ДН поворачивается обязательно в сторону отставания фазы возбуждающего тока. 3.3. Плоские антенные решетки поперечного излучения Плоские АР позволяют формировать узкий луч ДН в двух плоскостях, в отличие от линейных АР. Чаще всего в современных беспроводных системах телекоммуникаций применяются квадратные или прямоугольные плоские АР, иногда круглые, шестиугольные и др. Структура АР определяется требованиями, предъявляемыми к форме ДН, а также конструктивными особенностями решетки (виды ее элементов, система питания и т.п.). Рассмотрим эквидистантную, равноамплитудную, плоскую АР прямоугольной структуры (рис.3.5), расположенную в плоскости xoy. Ее элементы размещены в узлах прямоугольной сетки. 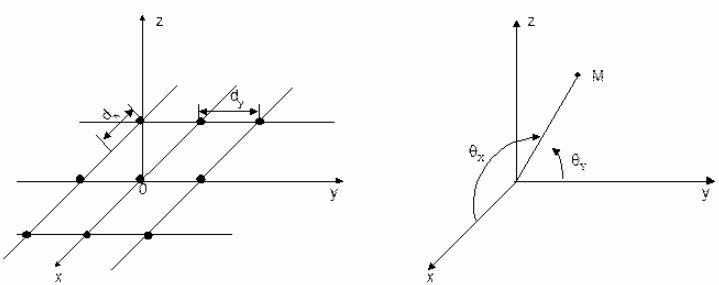 Рис.3.5 Плоская антенная решетка Пусть nx и ny – число излучателей в столбцах и рядах; dx и dy – расстояния между соседними излучателями по осям ox и oy соответственно; θx и θy – углы, отсчитываемые на точку наблюдения соответственно от осей ox и oy. Каждый столбец излучателей (столбец, будем считать, состоит из излучателей, расположенных вдоль оси ox) представляет собой прямолинейную, эквидистантную, равноамплитудную АР. Множитель системы такой АР, в соответствии с (3.2), можно записать в виде 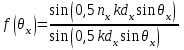 . (3.11) Если произвести эквивалентную замену каждого столбца плоской АР на одиночный гипотетический излучатель, с собственной ДН, совпадающей с выражением (3.11), то получим также линейную решетку, но ориентированную вдоль оси oy 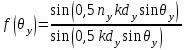 . (3.12) Множитель системы в сферической системе координат является функцией углов θ (меридиональная плоскость) и φ (экваториальная плоскость), а не θx и θy. Определяя связь между этим углами (по сути, связь между прямоугольной и сферическими системами координат), можно получить окончательное выражение для множителя системы плоской АР 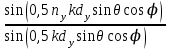 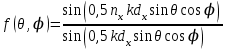 . . (3.13) Из выражения (3.13) следует, что сечение пространственной ДН плоской АР в главных плоскостях xozиyoz совпадает с формой ДН линейной АР. Основные выводы: – множитель плоской АР представляет собой произведение множителей двух линейных АР; первая из них представлена излучателями, образующими столбец, вторая – строку; – анализ множителя плоской АР изначально сводится к анализу множителей линейных АР, который можно производить совершенно независимо друг от друга. При введении фазового сдвига между токами, возбуждающими элементы решетки, выражение (3.13) принимает вид 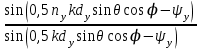 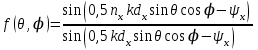 . .(3.14) Направления главных лепестков ДН можно определить, исходя из выражений для соответствующих линейных АР: 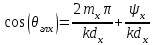 , где mx = 0, ±1, ±2, … (3.15) 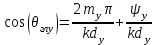 , где mx = 0, ±1, ±2, … (3.16) Из (3.15) и (3.16) следует, что независимое управление положением главного лепестка плоской АР можно осуществлять, изменяя величины фазовых сдвигов токов возбуждения в элементах строки (ψy) и столбца (ψx). При этом будет происходить отклонение главного лепестка либо от оси ox, либо от оси oy. Плоская АР будет иметь только один главный лепесток при условии, что каждая линейная АР (образующая строку или столбец) имеет только один главный лепесток, т.е. должны выполняться неравенства: 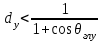 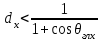 и . (3.17) Важное замечание: плоская АР (как и линейная АР) в случае использования СВ в качестве излучающих элементов решетки будет иметь два главных лепестка – в переднем и в заднем полупространствах. Для ограничения излучения в заднее полупространство, сзади линейной или плоской АР устанавливается рефлектор, представляющий собой плоское полотно (сплошной или сетчатой структуры), выполненное из металла. 3.4. Антенные решетки осевого излучения Рассмотрим линейную, эквидистантную АР, в которой ее элементы (в данном случае используются СВ) параллельны друг другу и расположены на одной оси (рис.3.6). Каждый вибратор излучает максимум поля вдоль оси ox. Если создать определенное фазовое распределение токов на вибраторах, то можно получить однонаправленное излучение вдоль оси ox. Дальнейшая задача состоит в определении зависимости направленных свойств рассматриваемой АР от ее размеров (длины) и параметров возбуждения. 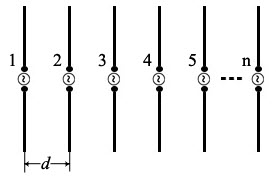 Рис.3.6 Антенная решетка осевого излучения Ее решение сводится к определению такого фазового сдвига между токами в вибраторах решетки, который позволил бы сформировать однонаправленное излучение вдоль оси решетки с максимальной эффективностью. Необходимый сдвиг фаз токов в элементах решетки (ψ) можно создать с помощью системы фазовращателей, однако схема питания при этом получается довольно сложной. Значительно упрощает ее конструкцию последовательное возбуждение вибраторов с помощью бегущей электромагнитной волны. Волна при этом распространяется от начала решетки (первый вибратор) к ее концу с определенной фазовой скоростью. Таким образом, первый вибратор создает начальное возбуждение волны, которая затем от элемента к элементу перемещается к последнему элементу. При этом ток в последующем вибраторе отстает по фазе от тока в предыдущем на величину ψ = βd, где d– расстояние между вибраторами, β = kc/v – коэффициент фазы, где k – волновое число, c – скорость света, v – фазовая скорость волны. Параметр c/v носит название коэффициент замедления. Если считать, что токи в вибраторах одинаковы, а их количество равно n, то: 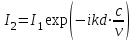 , ,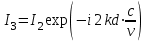 , ,… , 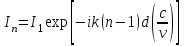 . (3.18) . (3.18)Так как каждый последующий вибратор возбуждается позже предыдущего, но находится ближе к точке наблюдения, то сдвиг фаз между полями соседних вибраторов в этой точке (фаза поля первого вибратора принимается за нулевую) равен 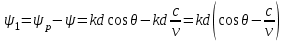 . (3.19) . (3.19)Сдвиг фаз между полями крайних вибраторов определяется как Ψn = (n – 1)kd(cosθ – c/v) . (3.20) Учитывая предыдущие рассуждения, можно получить формулу для ХН АР в меридиональной плоскости (плоскость вектора Е) 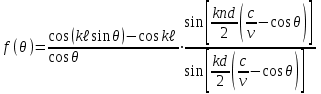 . (3.21) . (3.21) В экваториальной (азимутальной) плоскости (плоскость вектора H) СВ не обладает направленными свойствами, поэтому ХН АР в этой плоскости имеет вид 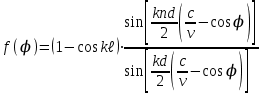 . (3.22) . (3.22)Как видно из (3.22), ХН в плоскости Н определяется только множителем системы fс(φ). В плоскости Е ХН зависит также и от направленных свойств одного элемента решетки, но, в основном, определяется множителем системы fc(θ). Поэтому при анализе направленных свойств АР следует рассматривать только этот множитель. Данная АР излучает максимум поля вдоль своей оси, поэтому она получила название «антенная решетка осевого излучения». В данной решетке результирующее поле формируется за счет волны, перемещающейся от ее первого элемента к последующему, поэтому она также получила название «антенна бегущей волны», или АБВ. Важно! Направленные свойства АБВ зависят от числа элементов решетки n, расстояния между ними d и от фазовой скорости питающей волны v. Возможна работа АБВ в трех режимах: 1) v = с; c/v = 1 (волна свободного пространства); 2) v > с; c/v < 1 (быстрая волна); 3) v < с; c/v >1 (медленная волна). В режиме волны свободного пространства множитель системы максимален и равен n при θ = 0°, выражение для ХН имеет вид 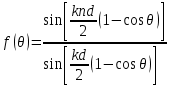 , (3.23) , (3.23)а ДН имеет вид, показанный на рис.3.7. 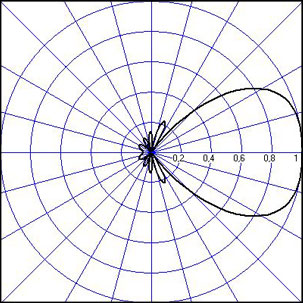 Рис.3.7 Диаграмма направленности решетки в режиме волны свободного пространства Уровень первого бокового лепестка ξ1 = 0,214, т.е. такой же, как у синфазной линейной АР поперечного излучения (см. параграф 3.2). Ширина главного лепестка ДН по нулевой мощности излучения (при малых значениях λ/L, где L=(n– 1)d – длина решетки) определяется как 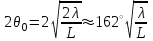 . (3.24) . (3.24)Ширина ДН по половинной мощности может быть определена по приближенной формуле 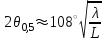 . (3.25) . (3.25)Сравнивая АБВ с равномерной синфазной АР, следует отметить, что хотя ее ДН получается шире, чем у синфазной АР такой же длины, но зато один ряд вибраторов, возбуждаемых бегущей волной тока, обладает направленными свойствами в любой плоскости, проходящей через ось антенны. В тоже время один ряд синфазной АР обладает направленными свойствами только в одной плоскости. Если элементы АБВ не обладают направленным действием или оно невелико, то ее ДН можно считать осесимметричной. При этом ее КНД при L/λ >1 можно определить по формуле D 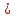 4L /λ. (3.26) 4L /λ. (3.26)В режиме быстрой волны ХН множителя системы имеет вид 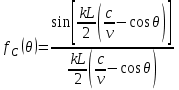 . (3.27) . (3.27)Из (3.27) видно, что условие cosθ = c/v может выполняться при двух значениях угла θ = ± θmах, следовательно, имеются два направления максимального излучения, не совпадающие с осью антенны, ДН показана на рис.3.8. Данный режим работы является невыгодным, так как направленные свойства антенны ухудшаются. Однако антенны, работающие в таком режиме, находят применение для формирования ДН специальной формы, а также ее качания (сканирования) в определенных секторах углов. 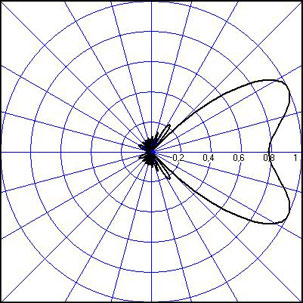 Рис.3.8 Диаграмма направленности решетки в режиме быстрой волны В режиме медленной волны отсутствует направление, в котором поля отдельных элементов антенны складываются синфазно, так как ни при каком значении θ отношение c/v не может стать равным cosθ и сдвиг фаз не может обратиться в нуль. Наименьший фазовый сдвиг между полями отдельных вибраторов Ψmin= kd(c/v - 1) получается в направлении θ=00, т.е. вдоль оси антенны. Поля отдельных вибраторов в точке наблюдения, лежащей в направлении θ =00, в данном случае складываются геометрически. Анализ выражения для ХН (3.23) показывает, что уменьшение фазовой скорости, начиная от v=c, сопровождается постепенным сужением главного лепестка ДН и ростом боковых лепестков. Излучение в главном направлении θ=00 сначала растет, достигая максимума при некоторой определенной (для данного значения L=nd) величине c/v, а затем начинает уменьшаться и обращается в нуль при критической величине c/v 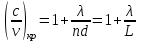 . (3.28) . (3.28)Сужение главного лепестка ДН приводит к росту КНД антенны, а увеличение уровня боковых лепестков – к его уменьшению. При увеличении c/v, начиная от c/v = 1, сначала увеличивается КНД из-за сужения ДН. После достижения некоторой определенной величины c/v дальнейший ее рост приводит к уменьшению КНД из-за увеличения уровня боковых лепестков. Следовательно, имеется оптимальная величинаc/v(при заданной длине антенны L), при которой КНД достигает максимального значения. Оптимальную величинуc/v при заданной длине антенны L можно рассчитать по формуле 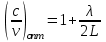 . (3.29) Оптимальную длину антенны при заданной фазовой скорости можно рассчитать по формуле 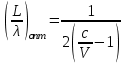 . (3.30) . (3.30)Как видно из (3.30), оптимальная длина антенны увеличивается при увеличении фазовой скорости. В случае ψn = ψnопт КНД определяется по формуле 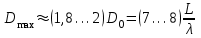 , (3.31) где D0 – КНД антенны бегущей волны данной длины при с/v = 1. ДН АБВ с пониженной фазовой скоростью, имеющей оптимальную длину, изображена на рис.3.9. 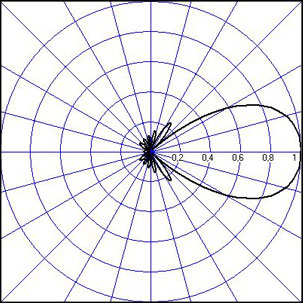 Рис.3.9 Диаграмма направленности решетки в оптимальном режиме Получение максимального значения напряженности поля в точке приема, лежащей на продолжении оси решетки (θ = 0°), получается тогда, когда величина результирующего сдвига фаз между полями, создаваемыми крайними (первым и последним) элементами решетки, равна 180°, т.е. поля должны находиться в противофазе. Таким образом, условием получения максимального КНД является 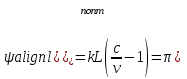 , (3.32) , (3.32)Ширина главного лепестка ДН по нулевой мощности излучения решетки, работающей в оптимальном режиме, определяется по формуле 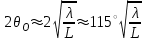 . (3.33) . (3.33)Сравнивая (3.33) с (3.24), видно, что в оптимальном режиме АБВ имеет ДН в 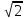 раз уже, чем антенна той же длины при c/v = 1. раз уже, чем антенна той же длины при c/v = 1. Ширина главного лепестка ДН по половинной мощности излучения может быть приближенно определена (для антенны, у которой L/λ »1) по формуле 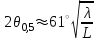 . (3.34) . (3.34)Уровень первого бокового лепестка ДН оптимальной антенны равен ξ1=0,33. При увеличении длины антенны по сравнению с оптимальной излучение в главном направлении уменьшается и растут боковые лепестки. При L = 2Lопт излучение в главном направлении полностью пропадает. При уменьшении длины антенны по сравнению с оптимальной главный лепесток ДН расширяется, уровень боковых лепестков уменьшается. Для того чтобы ДН становилась уже, надо увеличивать длину антенны. Вместе с тем, чтобы при удлинении АБВ ее длина оставалась оптимальной, необходимо увеличивать фазовую скорость волны в антенне. Основные выводы: – АР позволяют формировать узкие ДН, также они позволяют управлять направлением главного лепестка ДН; – направленные свойства АР зависят от числа элементов, межэлементных расстояний и параметров возбуждения элементов; – ХН АР с однотипными элементами представляет собой произведение ХН одного элемента на множитель системы; – основной вклад в результирующую ДН (при условии использования слабонаправленных элементов) вносит множитель системы; – линейные АР, состоящие из СВ, обладают направленными свойствами только в меридиональной плоскости (в плоскости вектора E); в экваториальной плоскости (в плоскости вектора H) направленными свойствами они не обладает; – линейные АР, состоящие из СВ, формируют два главных лепестка, перпендикулярных оси решетки (при условии синфазного возбуждения элементов); – при введении фазового сдвига между токами, возбуждающих элементы решеток, главный лепесток ДН поворачивается в сторону отставания фазы; – для формирования однонаправленного излучения позади линейных АР, состоящих из СВ, необходимо устанавливать рефлектор; – плоские АР формируют узкие ДН в обеих плоскостях; – плоские АР, состоящие из СВ, излучают два главных лепестка, перпендикулярных полотну решетки (при условии синфазного возбуждения элементов); – изменяя фазы токов, питающих элементы решетки, можно управлять направлением главного лепестка ДН; – для формирования однонаправленного излучения позади плоских АР, состоящих из СВ, необходимо устанавливать рефлектор; – АР продольного (осевого) излучения формируют главный лепесток ДН вдоль своей оси; – для однонаправленного излучения вдоль оси решетки необходимо создать определенное фазовое распределение между токами, возбуждающих ее элементы; – в АР продольного излучения можно устанавливать три режима ее работы: режим волны свободного пространства, режим медленной волны, режим быстрой волны; – формирование максимального излучения в главном направлении решетки происходит при разности фаз между первым и последним элементом решетки, равным 180 градусов; – максимальное значение КНД получается в режиме медленной волны, при установлении в решетке заданной длины такой фазовой скорости, которая является для нее оптимальной. |
