рк1. 2. слабонаправленное излучение симметричных вибраторов краткая теория симметричного вибратора
 Скачать 1.59 Mb. Скачать 1.59 Mb.
|
|
4. ИЗЛУЧЕНИЕ ВОЗБУЖДЕННОЙ ПОВЕРХНОСТИ 4.1. Свойства возбужденной поверхности Узкая ДН может быть сформирована при помощи антенны, представляющей собой излучающую поверхность, т.е. поверхность, на которой распределены взаимно перпендикулярные составляющие векторов Е и Н. Такая возбужденная поверхность называется апертурой. По сути, апертура – это часть фронта волны, ограниченная размерами раскрыва антенны, и активно участвующая в излучении (или приеме) электромагнитного поля. Апертуры бывают разной формы и зависят от конфигурации излучающего отверстия или отражающей или преломляющей электромагнитные волны поверхности. Возбужденную поверхность рассматривают как совокупность элементарных площадок, называемых источниками Гюйгенса. Существующие на элементарной площадке dSзначения векторов поля Еуи Hх на основании принципа эквивалентных токов можно представить как суперпозицию полей двух взаимно перпендикулярных поверхностных токов – электрического Iэ и магнитного Iм. Ввиду малости размеров площадки совокупность указанных токов можно рассматривать как два взаимно перпендикулярных элементарных диполя длиной dyи dxс токами Iэи Iм (рис.4.1). 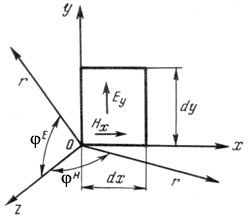 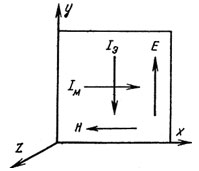 Рис.4.1 Источник Гюйгенса Излучение источника Гюйгенса направлено по нормали к элементарной площадке, его ХНти в обеих плоскостях одинаковы и определяются по формулам: 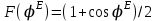 в плоскости Е , 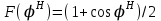 в плоскости Н . (4.1) Таким образом, ДН источника Гюйгенса одинаковы в обеих плоскостях и имеют форму кардиоиды (рис.4.2). 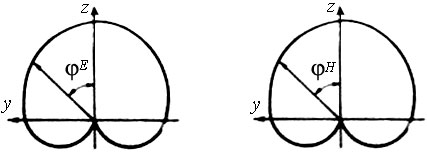 Рис.4.2 Диаграммы направленности источника Гюйгенса Амплитудная ДН источника Гюйгенса является слабонаправленной, поэтому практически не влияет на форму основного и первых боковых лепестков ДН остронаправленных антенн с плоским излучающим раскрывом. Исходя из этого, основной вклад в результирующую ДН возбужденного раскрыва вносит не направленность одного источника Гюйгенса, а совокупное действие всех источников, расположенных на рассматриваемой поверхности. Таким образом, возбужденную поверхность можно рассматривать, как плоскую АР поперечного излучения, состоящую из бесконечного числа элементов, расстояние между которыми стремится к нулю. В общем случае, как амплитуда, так и фаза возбуждающего поля могут являться функциями координат точки излучающей поверхности, т.е. 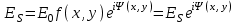 , (4.2) где Es – комплексная амплитуда возбуждающего поля в данной точке прямоугольной возбужденной поверхности; E0 – амплитуда возбуждающего поля в центре антенны; f(x,у) – функция, характеризующая зависимость амплитуды возбуждающего поля от координат (амплитудное распределение); ψ(x,y) – функция, определяющая зависимость фазы возбуждающего поля от координат точки излучающей поверхности (фазовое распределение). Следует иметь в виду, что в ряде случаев амплитудное или фазовое распределения бывают функциями только одной координаты. Антенны типа излучающей поверхности особенно широко применяются в диапазоне сантиметровых волн (антенна в виде открытого конца волновода, рупорные антенны, линзовые антенны, зеркальные антенны и др.). 4.2. Излучение плоского раскрыва Рассмотрим наиболее простой случай возбужденной поверхности – идеальную излучающую поверхность (идеальную плоскую антенну), которая представляет собой синфазную равноамплитудную АР поперечного излучения из элементов Гюйгенса (рис.4.3). Стороны прямоугольной поверхности обозначим через a и b. Вектор Е параллелен стороне b, а вектор Н – стороне а. 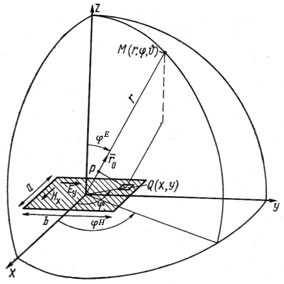 Рис.4.3 Идеальная излучающая поверхность Идеальной плоской антенной называется плоская возбужденная поверхность, в каждой точке которой тангенциальные составляющие векторов Е и Н имеют одинаковые направления, амплитуды и фазы, т.е. не зависят от координат. Выражение для расчета ХН идеальной плоской антенны в плоскости Е (плоскости yoz) имеет вид 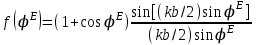 . (4.3) Выражение для расчета ХН идеальной плоской антенны в плоскости Н (плоскости yoz) имеет вид 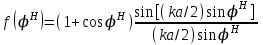 . (4.4) Как видно из (4.3) и (4.4), ХН идеальной плоской антенны в обеих плоскостях (при условии a = b) одинаковы и состоят из двух множителей. Первый множитель (1+cosφ) – ХН одного элемента излучающей поверхности (источника Гюйгенса). Этот множитель определяет однонаправленные свойства возбужденной поверхности в плоскостях Е и Н. Второй множитель – множитель системы, который определяет совокупное действие всех источников Гюйгенса, расположенных на рассматриваемой поверхности. Сравнив (4.3), (4.4) с (3.1) и (3.2), можно прийти к выводу, что существует явная аналогия между свойствами возбужденной поверхности и АР: ХН возбужденной поверхности определяется как произведение ХН одного элемента на множитель решетки. Множитель системы при изменении углов φEи φH изменяется значительно быстрее, чем первый множитель. Поэтому ХН идеальной плоской антенны, в основном, определяется множителем системы. Так как источник Гюйгенса излучает с максимальной интенсивностью в направлении нормали к своей поверхности, то направления максимумов множителя системы и ХН источника Гюйгенса совпадают. Поэтому идеальная плоская антенна излучает с максимальной интенсивностью в направлении к своей нормали. На рис.4.4 показана ДН идеальной излучающей поверхности, она имеет многолепестковый характер, что подтверждает – множитель системы этой антенны незначительно отличается от аналогичного множителя синфазной равноамплитудной АР. 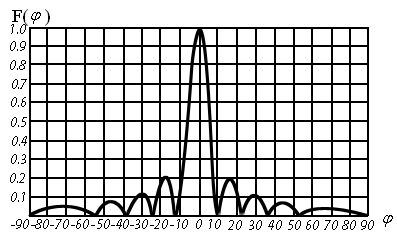 Рис.4.4 Диаграмма направленности идеальной излучающей поверхности Таким образом, ХН этих антенн (при малом расстоянии между элементами решетки) по существу отличаются только множителями, характеризующими направленные свойства одного элемента антенны. Как и в случае антенных решеток, направления, в которых отсутствует излучение, находится из условия равенства нулю числителей в выражениях (3.3), (3.4): 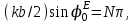 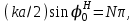 (4.5) (4.5)где N=1,2,3, …, о 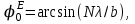 ткуда ткуда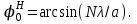 (4.6) Направления нулевого излучения отсутствуют, если λ > а или λ > b. Направлений нулевых излучений, т.е. боковых лепестков, тем больше, чем больше относительная ширина антенны (a/λ или b/λ). При больших размерах излучающих поверхностей (a/λ >>1 и b/λ>>1) ширина ДН идеальной плоской антенны по нулевому излучению определяется по формулам: 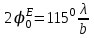 в плоскости Е ; в плоскости Е ; 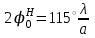 в плоскости Н . (4.7) Ширина ДН идеальной плоской антенны по половинной мощности определяется по формулам: 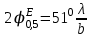 в плоскости Е ; 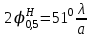 в плоскости Н . (4.8) Сравнивая (4.7), (4.8) с (3.6), (3.7), видно, что имеется аналогия между идеальной возбужденной поверхностью и синфазной АР, состоящей из вибраторов (при условии, что их число n велико). ДН идеальной плоской антенны в данной плоскости тем уже, чем больше размер антенны, параллельный этой плоскости. Ширина ДН в данной плоскости не зависит от размера антенны, перпендикулярного этой плоскости. Уровень первого лепестка ДН идеальной плоской антенны ξ1 = 0,214. Анализ показывает, что в пределах главного лепестка ДН идеальной плоской антенны сосредоточено около 82% излучаемой мощности; в боковых лепестках сосредоточено приблизительно 18% излучаемой мощности. 4.3.Влияние амплитудного распределения на направленные свойства плоского раскрыва На практике, при конструировании апертурных антенн, используются возбужденные поверхности с неравномерным амплитудным распределением поля (в случае прямоугольного раскрыва) либо вдоль одной стороны поверхности, либо вдоль обеих сторон. Наиболее типичный случай – использование в качестве облучателя зеркально-параболической антенны прямоугольного волновода, возбуждаемого волной типа H10. Поэтому рассмотрим синфазную прямоугольную излучающую поверхность с косинусоидальным амплитудным распределением поля вдоль оси ох и равномерным амплитудным распределением поля вдоль оси оy, что соответствует волне H10. Вид распределения поля по сторонам прямоугольного раскрыва показан на рис.4.5. 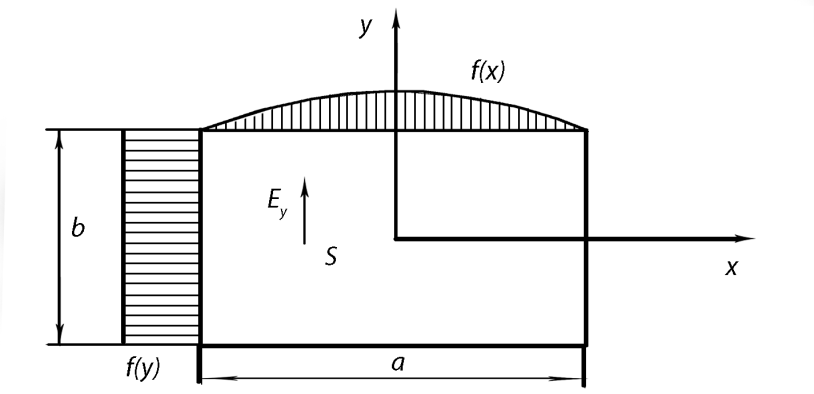 Рис.4.5 Неравномерное амплитудное распределение поля по сторонам прямоугольного раскрыва Так как распределение возбуждающего поля вдоль оси оу в данном случае такое же, как у идеальной антенны (т.е. равномерное), то ХН рассматриваемой излучающей поверхности в плоскости вектора Е (плоскости yoz) не отличается от ХН идеальной плоской антенны в этой плоскости. Вдоль оси ох полераспределено неравномерно: в середине оно максимально, к краям спадает до нуля; закон изменения амплитуды поля имеет вид 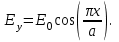 (4.9) Выражение для нормированной ХН в плоскости вектора Н (плоскость xoz) имеет вид 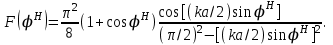 (4.10) Сравнивая (4.10) с (4.4), видно, что, по сравнению с идеальной плоской антенной, в данном случае изменился вид множителя системы. Ширина главного лепестка ДН по нулевому излучению в плоскости вектора Н определяется по формуле 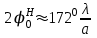 , (4.11) а по половинной мощности – по формуле 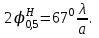 (4.12) Ширина главного лепестка ДН в плоскости вектора E остается такой же, как и у идеального раскрыва. Таким образом, при переходе от равномерного амплитудного распределения к распределению, спадающему к краям излучающей поверхности по закону косинуса, ширина ДН в соответствующей плоскости увеличивается примерно в 1,5 раза. Одновременно с расширением главного лепестка ДН уменьшаются уровни боковых лепестков: уровень первого бокового лепестка составляет ξ1 = 0,066, что в 3,2 раза меньше, по сравнению с идеальным раскрывом. Расширение ДН объясняется тем, что в соответствии с амплитудным распределением по мере удаления от центра антенны в направлении оси ох возбуждение элементарных площадок становится слабее. Очевидно, что поля, создаваемые близкими к краю поверхности площадками, из-за своей малости почти не влияют на величину результирующего поля антенны. Следовательно, уменьшение амплитуды возбуждающего поля к краям антенны эквивалентно уменьшению соответствующего размера антенны с равномерным распределением амплитуды возбуждающего поля. Таким образом, можно сделать вывод: чем резче спадает амплитуда возбуждающего поля к краям излучающей поверхности, тем шире главный лепесток ДН и тем меньше уровень боковых лепестков. Это же положение может быть распространено и на АР. Данное свойство излучающих поверхностей находит широкое практическое применение. Так, в тех случаях, когда требуются ДН с низким уровнем боковых лепестков, добиваются резко спадающего к краям антенны амплитудного распределения. Однако при этом расширяется главный лепесток ДН. 4.4.КНД излучающей поверхности В случае идеальной плоской антенны выражение для КНД имеет вид 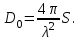 (4.13) КНД идеальной плоской антенны тем больше, чем больше площадь этой антенны и чем короче длина волны. КНД антенны обратно пропорционален квадрату длины волны при постоянной площади антенны. Легко видеть, что с укорочением длины волны облегчается построение антенн с высоким КНД. В случае неравномерного амплитудного распределения 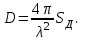 (4.14) где SД - действующая (эффективная) площадь антенны. Выражая КНД излучающей поверхности с произвольным распределением возбуждающего поля через КНД идеальной плоской антенны, получаем 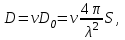 (4.15) где D0 – КНД идеальной плоской антенны; ν= SД/S – коэффициент использования поверхности раскрыва (КИП). Величина КИП раскрыва зависит от вида амплитудного и фазового распределения возбуждающего поля. КИП раскрыва тем меньше, чем резче амплитуда возбуждающего поля спадает к краям антенны. В случае косинусоидального амплитудного распределения КИП равен 0,81, тогда КНД определяется как 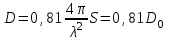 . (4.16) Уменьшение КНД излучающей поверхности со спадающим к краям амплитудным распределением по сравнению с идеальной излучающей поверхностью объясняется тем, что при одинаковой излучаемой мощности напряженность поля первой антенны в главном направлении будет меньше, чем напряженность поля второй антенны в этом же направлении, так как ДН первой антенны шире, чем второй. В случае реальных излучающих поверхностей эффективная поверхность антенны SД всегда меньше ее геометрической площади S. Можно сказать, что действующей площадью реальной антенны называется площадь такой идеальной плоской антенны (излучающей поверхности с равномерным амплитудным распределением и синфазным возбуждением), КНД которой равен КНД данной реальной антенны. 4.5. Влияние фазового распределения на направленные свойства плоского раскрыва Несинфазность излучающей поверхности может быть присуща данной антенне вследствие особенностей ее устройства, либо вызвана неточным выполнением антенны. Фазовые искажения ухудшают направленные свойства антенны. Однако в некоторых случаях на излучающей поверхности специально устанавливают определенный закон распределения фазы для получения ДН специальной формы или управления ДН (изменение положения ДН в пространстве). В самом общем случае фазовое распределение может являться функцией двух координат. Однако для упрощения исследования обычно рассматривают зависимость фазы от каждой координаты в отдельности. Если начало прямоугольной системы координат поместить в центре прямоугольной излучающей поверхности, то распределение фазы поля на излучающей поверхности (по раскрыву) антенны имеет вид 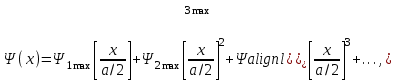 (4.17) где ψ1max, ψ2max, ψ3max и т.д. – максимальные фазовые сдвиги соответствующих составляющих фазового распределения, получающиеся на краях излучающей поверхности x = ±a/2, где а – размер поверхности (раскрыва) антенны. Монотонные законы изменения фазы возбуждающего поля, как правило, могут быть с достаточной точностью представлены тремя первыми членами данного ряда: линейным, квадратичным и кубическим. В некоторых случаях фазовое распределение антенны хорошо описывается одним членом ряда. Рассмотрим влияние на направленные свойства антенны наиболее простых фазовых распределений: линейного, квадратичного и кубического. При этом будем полагать, что амплитуда возбуждающего поля не зависит от координат. Линейное фазовое распределение При линейном распределении фазы ψ(x) = ψ1max(2x/a), напряженность возбуждающего поля изменяется по закону 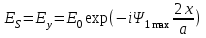 . (4.18) Вид распределения поля вдоль стороны а раскрыва показан на рис.4.6,а. Так как фаза возбуждающего поля изменяется только вдоль размера а антенны, то интересно исследовать направленные свойства антенны только в плоскости xoz (рис.4.6,б). 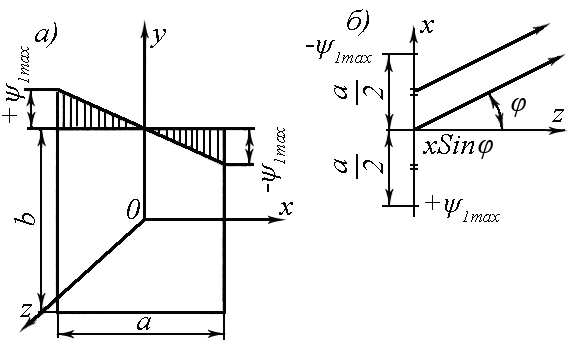 Рис.4.6 Линейный закон изменения фаз вдоль стороны а раскрыва Для возбужденной поверхности с линейным фазовым распределением ХН раскрыва рассчитывается как 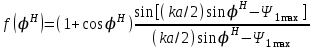 . (4.19) Направление максимального излучения находится как 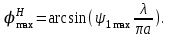 (4.20) Таким образом, следует, что ДН раскрыва с линейным фазовым распределением поворачивается, величина угла поворота определяется величиной фазового сдвига. Поворот ДН происходит в сторону отставания фазы. Аналогия между раскрывом с линейным фазовым распределением и несинфазной АР очевидна – свойства у них одинаковые. Квадратичное фазовое распределение При квадратичном распределении фазы ψ(x)=ψ2max(2x/a)2, напряженность возбуждающего поля изменяется по закону 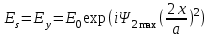 . (4.21) Вид распределения поля вдоль стороны а раскрыва показан на рис.4.7. 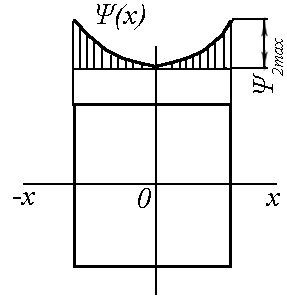 Рис.4.7 Квадратичный закон изменения фазы вдоль стороны а раскрыва Вследствие симметричности фазового распределения относительно центра излучающей поверхности, ДН не поворачивается, причем она остается симметричной при любых значениях ψ2max. Влияние квадратичного изменения фазы на направленные свойства излучающей поверхности проявляется в следующем: – исчезают нули между лепестками ДН; – уровень боковых лепестков увеличивается: главный лепесток ДН расширяется и при больших значениях ψ2max боковые лепестки полностью поглощаются расширяющимся главным лепестком; – при значениях сдвигов фаз ψ2max ≥ π происходит раздвоение главного лепестка: появляются два направления максимального излучения, излучение в направлении нормали уменьшается. Таким образом, квадратичное фазовое распределение приводит к искажению ДН и ухудшению направленных свойств антенны. При максимальных сдвигах фаз, не превышающих 45°, ДН как по ширине основного лепестка по половинной мощности, так и по уровню боковых лепестков почти не отличается от ХН идеальной плоской антенны. ДН для нескольких значений фазовых сдвигов приведены на рис.4.8. 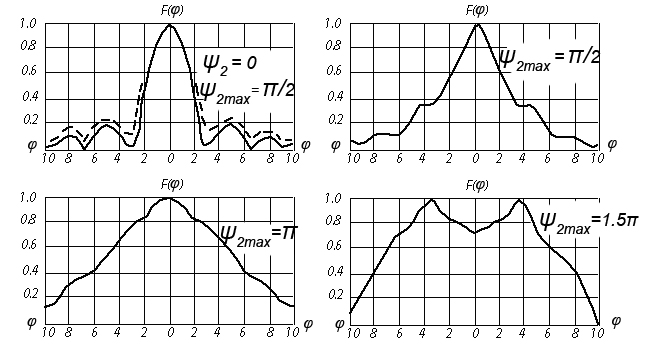 Рис.4.8 Диаграммы направленности площадки с квадратичным фазовым распределением Кубическое фазовое распределение При кубическом распределении фазы ψ(x)=ψ3max(2x/a)3, напряженность возбуждающего поля изменяется по закону 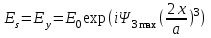 . (4.22) Вид распределения поля вдоль стороны а раскрыва показан на рис.4.9. Вследствие несимметричности фазового распределения (как и в случае линейных фазовых искажений), ДН раскрыва поворачивается, поворот происходит в сторону отставания фазы. При небольших значениях ψ3max(менее 180 градусов) угол отклонения ДН определяется как 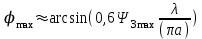 . (4.23) . (4.23) ДН раскрыва с кубическим фазовым распределением показана на рис.4.10. Все выводы относительно влияния различных фазовых распределений на направленные свойства плоского раскрыва относятся к случаю равномерного распределения амплитуды возбуждающего поля вдоль его сторон. 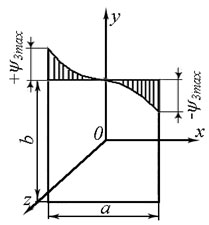 Рис.4.9 Кубический закон изменения фазы вдоль стороны а раскрыва 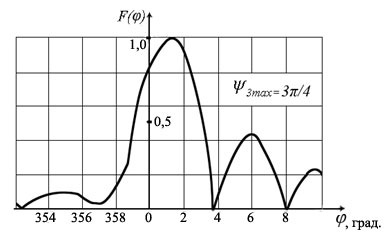 Рис.4.10 Диаграмма направленности раскрыва с кубическим фазовым распределением При спадающем к краям распределении влияние изменения фазы на ДН уменьшается. Поскольку различные законы изменения фазы связаны с ухудшением направленных свойств раскрыва, то при наличии фазовых искажений его КИП уменьшается. Основные выводы: – плоская возбужденная поверхность (раскрыв, или апертура) формирует узконаправленную ДН; – раскрыв представляет собой совокупность бесконечного числа элементарных площадок, называемых источниками Гюйгенса; – источник Гюйгенса имеет ДН в виде кардиоиды, т.е. обладает однонаправленными свойствами, причем в обеих главных плоскостях; – ХН раскрыва представляет собой произведение ХН источника Гюйгенса на множитель системы; – направленные свойства раскрыва зависят от размеров его сторон, амплитудного и фазового распределения вдоль них; – эффективность излучения раскрыва определяется величиной его КИП. СПИСОК ЛИТЕРАТУРЫ Основная литература 1.Антенно-фидерные устройства и распространение радиоволн. Под редакцией Ерохина Г.А. - М.:Горячая линия - Телеком, 2004. 2.Ерохин Г.А., Чернышев О.В., Козырев Н.Д., Кочержевский В.Г. Антенно-фидерные устройства и распространение радиоволн. - М.:Радио и связь, 1996. 3.Антенны. Карл Ротхаммель - М.:Данвел, 2007. 4.Warren L. Stutzman , Gary A. Thiele. Antenna Theory and Design. 3rd Edition. John Wiley, 2012. 5.Ликонцев Д.Н. Конспект лекций по дисциплине “Распространение радиоволн и антенно-фидерные устройства мобильных систем связи” по направлению образования «Мобильные системы связи». – Т.: ТУИТ, 2012. 6.Ўзбекистон Республикасини янада ривожлантириш бўйича ҳаракатлар стратегияси тўғрисида. Ўзбекистон Республикаси Перзидентининг ПФ-4947-сон фармони. Тошкент, 2017 йил 7 феврал. 7. Мирзиёев Ш.М. Буюк келажагимизине мард ва олижаноб халқимиз билан бирга қурамиз. 2017. 8. Мирзиёев Ш.М. Қонун устуворлиги ва инсон манфаатларини таъминлаш – юрт тараққиёти ва халқ фаровонлигининг гарови. 2017. 9. Мирзиёев Ш.М. Эркин ва фаровон, демократик Ўзбекистон двалатини биргаликда барпо этамиз. 2017. Дополнительная литература 1. Ликонцев Д.Н. Антенно-фидерные устройства: Конспект лекций. – Т.: ТУИТ, 2002. 2. Драбкин А.Л., Зузенко В.Л., Кислов А.Г. Антенно-фидерные устройства. – М.: Советское радио, 1974. 3. Губенко В.А., Кан В.С. Исследование направленных свойств панельных антен: Учебный комплекс по дисциплине «Основы антенн». – Т.: ТУИТ, 2015. ОСНОВЫ АНТЕНН. ЧАСТЬ 1 УЧЕБНОЕ ПОСОБИЕ Рассмотрено на заседании кафедры СТРВ 24.04.2018 г. (протокол № 30) и рекомендовано к печати. Рассмотрено на Научно-методическом Совете ФТТ 01.05.2018 г. (протокол №9) и рекомендовано к печати. Рассмотрено на Научно-методическом Совете ТУИТ 23.05.2018 г. (протокол №10) и рекомендовано к печати.
Заказ № Печать Тираж Количество |
