23Понятие алгоритма. Необходимость уточнения понятия алгоритма. Алгоритмическая машина поста.
Алгоритм как абстрактная машина.
. Исторически термин «алгоритм» произошел от фамилии узбекского математика ix века мухаммада ибн муса ал-хорезми, который впервые сформулировал правила четырех основных арифметических действий. Поначалу именно эти правила назывались алгоритмами, затем этот термин получил дальнейшее развитие в первую очередь в математике – алгоритмом стал называться любой способ вычислений, единый для некоторого класса исходных данных. В связи с этим возникает вопрос: можно ли построить общее и точное определение алгоритма?
Можно сказать, что алгоритм – это точно определенная (однозначная) последовательность простых (элементарных) действий, обеспечивающих решение любой задачи из некоторого класса.
Однако данное утверждение нельзя принять в качестве строгого определения алгоритма, поскольку в нем использованы другие неопределяемые понятия – однозначность, элементарность и др. Понятие можно уточнить, указав перечень общих свойств, которые характерны для алгоритмов. К ним относятся: дискретность алгоритма, детерминированность алгоритма, элементарность шагов, направленность алгоритма, массовость алгоритма.
Понятие алгоритма, в какой-то мере определяемое перечислением свойств 1-5, также нельзя считать строгим, поскольку в формулировках свойств использованы термины «величина», «способ», «простой» и другие, точный смысл которых не установлен. Данное определение называют нестрогим (интуитивным) понятием алгоритма.
Интуитивное понятие алгоритма хотя и не обладало строгостью, но было настолько ясным, что практически до xx в. Не возникало ситуаций, когда математики разошлись бы в рассуждениях относительно того, является ли алгоритмом тот иной конкретный процесс. Положение существенно изменилось, когда были сформулированы такие проблемы, алгоритмическое решение которых было не очевидно. Действительно, для доказательства существования алгоритма необходимо просто решить данную задачу. Гораздо сложнее доказать факт невозможности построения алгоритма решения некоторой задачи – без точного определения алгоритма эта проблема теряет смысл.
Другим основанием, потребовавшим построения точного определения алгоритма, явилось неопределенность понятия «элементарность шага» при выполнении алгоритмических действий. Например, можно ли считать элементарным шагом взятие интеграла?
В тех ситуациях, когда задача допускает построение нескольких алгоритмов решения, с теоретической и с практической точек зрения оказывается существенным вопрос их сопоставления и выбора наиболее эффективного алгоритма, что также невозможно без строгого определения.
Таким образом, возникла необходимость в точном определении понятия «любой алгоритм», т.е. Максимально общем определении, под которое подходили бы все мыслимые виды алгоритмов. Попытки формулировки такого определения привели к появлению в 30-х годах теории алгоритмов как самостоятельной науки.
.
24Машина тьюринга. Устройство. Состояние машины. Конфигурация.
Машина тьюринга состоит из трех частей: ленты, считывающе-записывающей головки и логического устройства. Лента выступает в качестве внешней памяти; она считается неограниченной (бесконечной) - уже это свидетельствует о том, что машина тьюринга является модельным устройством, поскольку ни одно реальное устройство не может обладать памятью бесконечного размера.
Лента разбита на отдельные ячейки, однако, в машине тьюринга неподвижной является головка, а лента передвигается относительно нее вправо или влево. Другим отличием является то, что она работает не в двоичном, а некотором произвольном конечном алфавите а={δ, а1, ..., ап} - этот алфавит называется внешним. В нем выделяется специальный символ - δ, называемый пустым знаком. В каждую ячейку ленты может быть записан лишь один символ. Информация, хранящаяся на ленте, изображается конечной последовательностью знаков внешнего алфавита, отличных от пустого знака.
Головка всегда расположена над одной из ячеек ленты. Работа происходит тактами (шагами). В машине тьюринга реализуется система предельно простых команд обработки информации. Эта система команд обработки дополняется также предельно простой системой команд перемещений ленты: на ячейку влево, на ячейку вправо и остаться на месте, т.е. Адрес обозреваемой ячейки в результате выполнения команды может либо измениться на 1, либо остаться неизменным. Элементарность этих команд означает, что при необходимости обращения к содержимому некоторой ячейки, она отыскивается только посредством цепочки отдельных сдвигов на одну ячейку. Разумеется, это значительно удлиняет процесс обработки, зато позволяет обойтись без нумерации ячеек и использования команд перехода по адресу, т.е. Сокращает количество истинно элементарных шагов, что важно в теоретическом отношении.
Обработка информации и выдача команд на запись знака, а также сдвига ленты в машине тьюринга производится логическим устройством (лу). 
Понимать схему необходимо следующим образом: на такте i на один вход лу подается знак из обозреваемой в данный момент ячейки (аi), а на другой вход - знак, обозначающий состояние лу в данный момент (qi). В зависимости от полученного сочетания знаков (аi, qi} и имеющихся правил обработки лу вырабатывает и по первому выходному каналу направляет в обозреваемую ячейку новый знак (аi+1), подает команду перемещения головки (di+1 из r, l и s), а также дает команду на вызов следующего управляющего знака (qi+1). Таким образом, элементарный шаг (такт) работы машины тьюринга заключается в следующем: головка считывает символ из обозреваемой ячейки и, в зависимости от своего состояния и прочитанного символа, выполняет команду, в которой указано, какой символ записать (или стереть) и какое движение совершить. При этом и головка переходит в новое состояние.
Общее правило, по которому работает машина тьюринга, можно представить следующей записью: qiaj®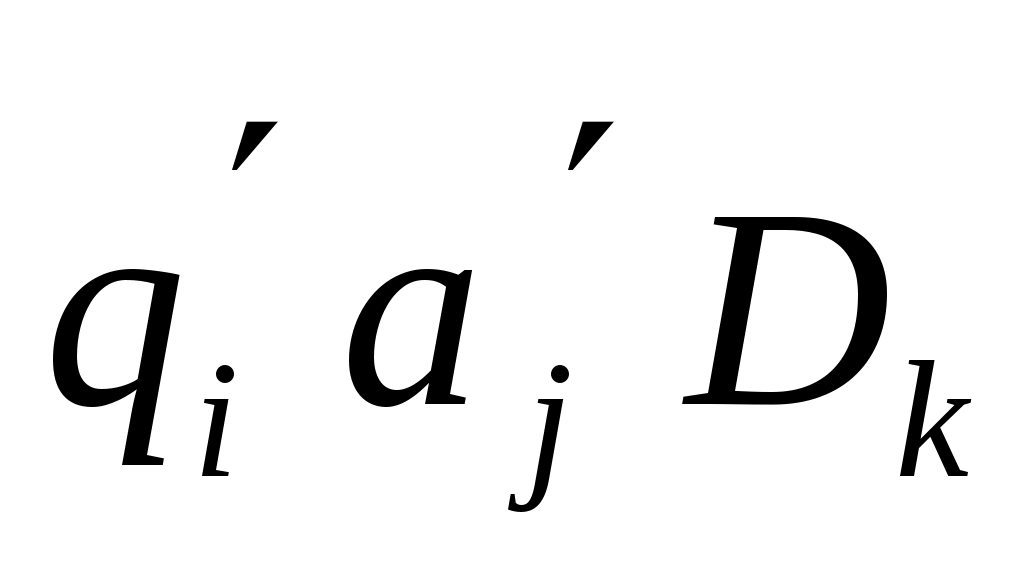 , т.е. После обзора символа аj головкой в состоянии qi, в ячейку записывается символ аj’, головка переходит в состояние qi', а лента совершает движение dk. , т.е. После обзора символа аj головкой в состоянии qi, в ячейку записывается символ аj’, головка переходит в состояние qi', а лента совершает движение dk.
Конкретная машина тьюринга задается перечислением элементов множеств а и q, а также, логической функцией, которую реализует лу, т.е. Набором правил преобразования. Ясно, что различных множеств a, q и логических функций может быть бесконечно много, т.е. И машин тьюринга также бесконечно много.
Совокупность состояний всех ячеек ленты, состояния лу и положение головки называется конфигурацией машины
25Нормальные алгоритмы Маркова. Сравнение алгорит-ких схем Маркова и Тьюринга.
По смыслу данный подход близок к идеям тьюринга, однако, в нем не используются представления о каких-либо машинах. Алгоритм задается системой подстановок, которые указывают, какие замены символов необходимо производить и в каком порядке эти подстановки должны следовать. Такой подход был предложен а. А. Марковым. В начале 50-х годов было введено понятие нормального алгоритма (сам марков называл их алгорифмами).
Рассмотрим некоторый алфавит а, содержащий конечное число знаков (букв). Введем ряд определений:
Слово - это любая конечная последовательность знаков алфавита.
Число символов в слове называется его длиной.
Слово, длина которого равна нулю, называется пустым.
Слово s называется подсловом слова q, если q можно представить в виде q=rst, где rut- любые слова в том же алфавите (в том числе и пустые).
Теперь можно определить понятие алгоритма (не являющееся строгим):
Алгоритмом в алфавите а называется эффективно вычислимая функция, областью определения которой служит какое-либо подмножество множества всех слов в алфавите а и значениями которой также являются слова в алфавите а.
В алгоритмах маркова в качестве элементарного шага алгоритма принимается подстановка одного слова вместо другого. Пусть в алфавите а построено исходное слово р, которое содержит подслово рr(в общем случае таких подслов в исходном слове может быть несколько), а также имеется некоторое слово pkв том же алфавите.
Подстановкой называется замена первого по порядку подслова рr исходного слова р на слово pk. Обозначается подстановка prpk.
Нормальный алгоритм маркова можно рассматривать как стандартную форму для задания любого алгоритма. Данная форма представления алгоритма важна не только с точки зрения проведения исследований в теории алгоритмов, но она послужила основой специализированного языка символьных преобразований в системах искусственного интеллекта.
Сопоставление алгоритмических моделей.
Некоторые теоретические проблемы (например, проблема алгоритмической разрешимости) и потребности практики (например, необходимость формулировки принципов работы устройств, производящих автоматизированную обработку информации) потребовали построения строгого определения алгоритма. Различные варианты решения проблемы привели к построению так называемых абстрактных алгоритмических систем (их называют также алгоритмическими моделями).
Все алгоритмические задачи принято делить на два больших класса: первый - это задачи, связанные с вычислением значения функции; второй - задачи, связанные с распознаванием принадлежности объекта заданному множеству (что равносильно получению ответа на вопрос: обладает ли объект заданным свойством?). В первом случае алгоритм qначинает работать с исходными данными - словом р, составленным на основе алфавита а, и за конечное число шагов (преобразований) он должен остановиться и выдать результат pk = fq(p). Результат зависит (является функцией) от исходного слова, а также последовательности обработки, т.е. Самого алгоритма. При этом вычисление понимается в широком смысле - как алфавитное преобразование.
В задачах, отнесенных ко второму классу, в результате выполнения алгоритма получается ответ на вопрос: «истинно ли высказывание, что хм »?
Таким образом, все модели оказываются эквивалентными, вчем виден глубокий смысл, так как результат обработки информации, безусловно, определяется характером функции (алгоритмом) и входными данными, но не зависит от вида алгоритмической модели.
26Основные понятия теории графов. Степень вершины графа. Ориентированные графы, связные графы и компоненты связности. Понятие взвешенного графа. Способы задания графа.
Граф - это система некоторых объектов вместе с некоторыми парами этих объектов, изображающая отношения связи между ними. Графами удобно изображаются сети коммуникаций, дискретные многошаговые процессы, системы бинарных отношений, структурные химические формулы, различные схемы и диаграммы и др.
Неориентированный граф (соответственно ориентированный граф, или орграф) g – это система g = (v, е, f), состоящая из множества элементов v= {v}, называемых вершинами графа, множества элементов е = {е}, называемых ребрами, и отображения f: е -> v2, ставящего в соответствие каждому элементу е е неупорядоченную (соответственно упорядоченную) пару элементов vt> v2 v, называемых концами ребра е.
Вершины в графе могут отличаться друг от друга тем, скольким ребрам они принадлежат. Степенью вершины называется число ребер графа, которым принадлежит эта вершина. Степенью выхода вершины а ориентированного графа называют число выходящих из а ребер. Степенью входа вершины а ориентированного графа называется число входящих в а ребер.
Vе образует множество элементов графа; при этом предполагается, что еv = 0. Отображение f определяет отношение инцидентности ребра с каждым из своих концов. Для графа g = (v, е, f) употребляется также более короткое обозначение g = (v, е) без указания инцидентностей, которые определяются контекстом. По количеству элементов графы делятся на конечные и бесконечные.
Вершина, не инцидентная ни одному ребру, называется изолированной. Вершина, инцидентная ровно одному ребру, и само это ребро называются концевыми, или висячими. Ребро с совпадающими концами называется петлей. Две вершины, инцидентные одному и тому же ребру, называются соседними (или смежными). Два ребра, инцидентные одной и той же вершине, называются смежными. Ребра, которым поставлена в соответствие одна и та же пара вершин, называются кратными, или параллельными.
Два графа g1=(v1, e1, f 1) и g2= (v2, е2, f 2) называются изоморфными, если существуют взаимно однозначные отображения f: v1 <=> v2 и g: e1 <=> е2, сохраняющие инцидентность, т.е. Такие, что для всякого е е1 равенство f 1(е) = (v1, v2) влечет за собой равенство f 2(gе) = (fv1, fv2).
Способы задания графов связаны с различной формой задания функции f . Рассмотрим некоторые из них.
1) перечисление (список) ребер графа с указанием их концов и добавлением списка изолированных вершин.
2) матрица инциденций графа с b вершинами и р ребрами - прямоугольная матрица а = aij с b строками и р столбцами, строки которой соответствуют вершинам графа, а столбцы - ребрам, причем для неориентированного графа элемент матрицы aij равен 1, если вершина vi и ребро ej инцидентны, и равен 0 в противном случае. Для ориентированного графа aij = -1, если vi является началом дуги еj и aij = +1, если vi - конец дуги еj. В каждом столбце матрицы инциденций два ненулевых элемента, если ребро - не петля. Петле соответствует элемент, = 2.
3) матрица достижимости вершин графа с b вершинами - квадратная матрица в = bij размерности b, строки и столбцы которой соответствуют вершинам графа, причем неотрицательный элемент bij равен числу ребер, идущих из вершины vi в вершину vj . Для несмежных вершин соответствующий элемент матрицы равен 0.
4) матрица смежности вершин графа, с b вершинами - квадратная матрица в = bij размерности b, строки и столбцы которой соответствуют вершинам графа, причем
27Деревья. Эйлеровы графы. Полный граф, двудольный граф.
Полный граф, двудольный граф, n-мерный единичный куб.
Полным графом называется граф без кратных ребер (и иногда без петель), в котором любые две вершины соединены ребром (ориентированным или неориентированным). Полный неориентированный граф с b вершинами обозначается кb. Очевидно, граф кb содержит сь 2- b*(b - 1) / 2 ребер. Полный граф представляет бинарное отношение r: если r рефлексивно, то граф - с петлями; если r симметрично, то граф - неориентированный, если r антисимметрично, то – ориентированный.
Двудольным графом называется граф, вершины которого разбиты на два непересекающихся класса: v = v1úv2, а ребра связывают вершины только из разных классов - не обязательно все пары. Если же каждая из вершин класса v1 связана ребром с каждой вершиной класса v2, то граф называется полным двудольным и обозначается кm,n, где m = | v1|, n = | v2|. Очевидно, граф кm,n содержит (n+m) вершин и n*п ребер. На следующем рисунке 1.3. Под буквой а изображен двудольный граф, а под буквами б и в - полные двудольные графы к3,2 и к3?з (последний носит название "3 дома - 3 колодца").
Для рассмотрения понятия «дерево» введем в рассмотрение ряд определений.
Цепью называется последовательность вершин и ребер, образующая путь в соотнесенном неориентированном графе.
Связный граф, который становится несвязным при удалении любого ребра;
Выберем в дереве произвольную вершину а0 и назовем ее корнем, или вершиной нулевого яруса. Соседние вершины назовем вершинами первого яруса и т.д. - вершины, соседние вершинам (i -1)-го яруса, не отнесенные еще ни к одному ярусу, назовем вершинами i-го яруса. Каждая вершина дерева принадлежит ровно одному ярусу.
Очевидно, что номер яруса совпадает с расстоянием между его вершинами и корнем дерева. В силу свойства дерева каждая вершина 1-го яруса связана ребром ровно с одной вершиной (i -1) го яруса и не связана ребром ни с какой вершиной 1-го яруса (рис 1.5).
Такое представление дерева часто является удобным. Оно показывает, в частности, что в конечном дереве всегда существуют концевые вершины (например, вершины последнего яруса, но, возможно, и другие).
Если конечный четный граф связен, то нетрудно показать (например, индукцией по числу его элементарных циклов), что в нем существует простой (т.е. Не самопересекающийся по ребрам) цикл, содержащий все ребра графа. Такой цикл называется эйлеровым циклом, а обладающий им граф называется эйлеровым графом. Поскольку каждая вершина простого цикла имеет в нем четную степень (каждое прохождение через вершину по циклу использует два ребра, инцидентных этой вершине), то доказана следующая теорема.
Теорема эйлера. Для того чтобы конечный связный граф был эйлеровым, необходимо и достаточно, чтобы он был четным. В конечном несвязном четном графе все компоненты связности - эйлеровы графы.
Будем называть вершину ориентированного графа равновесной, если число дуг, входящих в вершину, равно числу дуг, исходящих из нее. Ориентированный граф назовем равновесным, если все его вершины равновесные.
Обход (неориентированного) эйлерова графа по эйлерову циклу ориентирует каждое ребро графа в направлении обхода. Ясно, что при такой ориентации эйлеров граф является равновесным. Пусть теперь дан равновесный граф.
28.Основные методы разработки эффективных алгоритмов: динамическое программирование, алгоритмы с возвратом, жадные алгоритмы.
Динамическое программирование.
Динамическое программирование применимо тогда, когда подзадачи не являются независимыми или же их взаимозависимость установить очень трудно. Алгоритм, основанный на динамическом программировании, решает каждую из подзадач всего один раз и запоминает ответ для нее в специальной таблице.
Динамическое программирование применяется к задачам оптимизации, то есть к таким, для которых существует большое количество решений, но их качество определяется каким либо фактором или параметром. Суть как раз и состоит в том, чтобы найти из всевозможных решений именно то, которое дает экстремум (максимум или минимум) этого параметра. Алгоритм, основанный на динамическом программировании, строится следующим образом:
1) описываем строение оптимального решения;
2) строим рекуррентное соотношение, связывающее задачу с ее подзадачами;
3) делаем обход дерева подзадач и вычисляем оптимальное значение искомого параметра для каждой из них, запоминая эти решения в таблице;
4) пользуясь полученной информацией, строим оптимальное решение.
Особенность динамического программирования заключается как раз в том, что подзадачи нужно решать только один раз, а при каждом последующем вызове рекурсивной процедуры для решения той же подзадачи достаточно просто прочитать данные из таблицы.
Алгоритмы с возвратом. Как правило, такие алгоритмы строятся на основе рекурсии. Эти алгоритмы отличаются от других тем, что ищут решения методом проб и ошибок, перебирая все или почти все варианты. Backtracking используется в тех случаях, когда более интеллектуальные решения невозможны. Количество таких задач ограничено. Для лучшего восприятия начнем с примеров. Примеры подберем не случайные, а такие, которые нагляднее всего реализовали следующие цели:
• поиск оптимума с полным перебором всех вариантов;
• поиск любого решения с выходом при его отыскании;
• поиск оптимального решения с оптимизацией полного перебора (отсечением вариантов, которые заведомо хуже ранее найденного оптимального решения).
Жадные алгоритмы. Этот класс алгоритмов намного проще и быстрее, чем динамическое программирование. Жадный алгоритм производит на каждом шаге локально оптимальный выбор, допуская, что итоговое решение окажется оптимальным. Однако это не всегда так, и потому иногда бывает, что жадный алгоритм в терминах вышеупомянутого определения есть не полноценным алгоритмом, а приблизительным алгоритмом. Но для большого числа алгоритмических задач жадные алгоритмы действительно дают оптимум.
29Понятие сложности алгоритма. Оценка сложности алгоритма.
Термин «алгоритм» появился в математике достаточно давно и использовался долго - под ним понималась процедура, позволявшая путем выполнения последовательности определенных элементарных шагов получать однозначный результат, не зависящий от того, кто эти шаги выполнял. Таким образом, само проведенное решение служило доказательством существования алгоритма. Однако был известен целый ряд математических задач, разрешить которые в общем виде не удавалось. Примерами могут послужить три древние геометрические задачи: о трисекции угла, о квадратуре круга и об удвоении куба - ни одна из них не имеет общего способа решения с помощью циркуля и линейки без делений.
Интерес математиков к задачам подобного рода привел к постановке вопроса: возможно ли, не решая задачи, доказать, что она алгоритмически неразрешима, т.е. Что нельзя построить алгоритм, который обеспечил бы ее общее решение? Ответ на это вопрос важен, в том числе, и с практической точки зрения, например, бессмысленно пытаться решать задачу на компьютере и разрабатывать для нее программу, если доказано, что она алгоритмически неразрешима. Именно для ответа на данный вопрос и понадобилось сначала дать строгое определение алгоритма, без чего обсуждение его существования просто не имело смысла. Построение такого определения, как уже знаем, привело к появлению формальных алгоритмических систем, что дало возможность математического доказательства неразрешимости ряда проблемПервые доказательства алгоритмической неразрешимости касались некоторых вопросов логики и самой теории алгоритмов. Оказалось, например, что неразрешима задача установления истинности произвольной формулы исчисления предикатов (т.е. Исчисление предикатов неразрешимо) - эта теорема была доказана в 1936 г черчем.
В 1946-47 гг. А.а. Марков и э. Пост независимо друг от друга доказали отсутствие алгоритма для распознавания эквивалентности слов в любом ассоциативном исчислении.
Другой пример алгоритмически неразрешимой задачи - проблема самоприменимости. Классическим ее примером является известный парадокс парикмахера. В некотором городе жил парикмахер, который был обязан брить всех тех и только тех жителей города, кто не бреет себя сам. Спрашивается, бреет ли этот парикмахер сам себя. Если нет, то он принадлежит к категории жителей, не бреющих себя, и поэтому должен брить себя. Противоположное предположение о том, что он бреет себя, тоже, как легко видеть, приводит к противоречию. Решение этого парадокса – принятое парикмахером обязательство невыполнимо.
Поэтому труднорешаемой (нерешаемой) задачей можно называть такую задачу, для которой не существует эффективного алгоритма решения. Эффективный алгоритм имеет не настолько резко возрастающую зависимость количества вычислений от входных данных, например ограниченно полиномиальную, т.е х находится в основании, а не в показателе степени. Такие алгоритмы называются полиномиальными, и, как правило, если задача имеет полиномиальный алгоритм решения, то она может быть решена на эвм с большой эффективностью. К ним можно отнести задачи сортировки данных, многие задачи математического программирования и т.п.
Развитие и совершенствование компьютерной техники повлекло за собой создание разнообразных алгоритмов, обеспечивающих решение многочисленных прикладных задач, причем даже для однотипных задач создавалось (и создается) много алгоритмов (программ). Подобные алгоритмы ранее были названы эквивалентными.
Временная сложность алгоритма - это функция, которая каждой входной длине слова n ставит в соответствие максимальное (для всех конкретных однотипных задач длиной п) время, затрачиваемое алгоритмом на ее решение.
Различные алгоритмы имеют различную временную сложность и выяснение того, какие из них окажутся достаточно эффективны, а какие нет, определяется многими факторами. Однако теоретики, занимающиеся разработкой и анализом алгоритмов, для сравнения эффективности алгоритмов предложили простой подход, позволяющий прояснить ситуацию. Речь идет о различии между полиномиальными и экспоненциальными алгоритмами.
Полиномиальным называется алгоритм, временная сложность которого выражается некоторой полиномиальной функцией размера задачи п.
Алгоритмы, временная сложность которых не поддается подобной оценке, называются экспоненциальными.
Различие между указанными двумя типами алгоритмов становятся особенно заметными при решении задач большого размера.
Задача считается труднорешаемой, если для нее не удается построить полиномиального алгоритма.
Остановимся на вопросе о выборе такой характеристики исходных данных, которая определяла бы время работы программы. Эта характеристика называется размером задачи. Для разных задач на время решения влияют разные свойства исходных данных. Так, для задач типа поиска минимума или упорядочивания заданных чисел, где каждое число рассматривается как единое целое, размером задачи является количество исходных чисел. Для задачи разложения на простые сомножители размером естественно считать величину числа. Выбор размера задачи основан на некотором, хотя бы общем представлении об алгоритме решения. Обратимся к задаче вычисления 2n. Учитывая, что возведение в степень будет выполняться путем последовательного умножения, выберем в качестве размера показатель степени n. Другим возможным кандидатом на роль размера является число цифр в результате. В нашей задаче число цифр в числе 2n практически пропорционально n, поэтому оба размера эквиваленты.
Следующий важный момент при оценке времени работы – отыскание тех частей программы, выполнение которых занимает основную долю всего времени работы. Известен экспериментальный факт, справедливый для подавляющего большинства программ: основная часть времени работы тратится на выполнение очень небольшой части текста программы. Такая часть программы называется внутренним циклом. Так как с самого начала мы требуем приближенной оценки времени работы, поэтому всей остальной частью программы можно пренебречь.
30Кодирование. Алфавитное неравномерное двоичное кодирование. Префиксные коды.
Для представления дискретных сообщений используется некоторый алфавит. Однако однозначное соответствие между содержащейся в сообщении информацией и его алфавитом отсутствует. В целом ряде практических приложений возникает необходимость перевода сообщения хода из одного алфавита к другому, причем, такое преобразование не должно приводить к потере информации. Введем ряд с определений.
Будем считать, что источник представляет информацию в форме дискретного сообщения, используя для этого алфавит, который в дальнейшем условимся называть первичным. Далее это сообщение попадает в устройство, преобразующее и представляющее его в другом алфавите - этот алфавит назовем вторичным.
Код Кодирование Декодирование Кодер Декодер
Алфавитное неравномерное двоичное кодирование. Префиксные коды.Знаки первичного алфавита кодируются комбинациями символов двоичного алфавита (т.е. 0 и 1), причем, длина кодов и длительность передачи отдельного кода, могут различаться. Длительности элементарных сигналов при этом одинаковы (to=t1=t). Очевидно, для передачи информации, в среднем приходящейся на знак первичного алфавита, необходимо время k(a,2)*t. Таким образом, задачу оптимизации неравномерного кодирования можно сформулировать следующим образом: построить такую схему кодирования, в которой суммарная длительность кодов при передаче (или суммарное число кодов при хранении) данного сообщения была бы наименьшей.
Неравномерный код с разделителем условимся, что разделителем отдельных кодов букв будет последовательность 00 (признак конца знака), а разделителем слов-слов - 000 (признак конца слова - пробел). Довольно очевидными оказываются следующие правила построения кодов:
Код признака конца знака может быть включен в код буквы, поскольку не существует отдельно (т.е. Кода всех букв будут заканчиваться 00);
Коды букв не должны содержать двух и более нулей подряд в середине (иначе они будут восприниматься как конец знака);
Код буквы (кроме пробела) всегда должен начинаться с 1;
Разделителю слов (000) всегда предшествует признак конца знака; при этом реализуется последовательность 00000 (т.е., если в конце кода встречается комбинация ...000 или ...0000, они не воспринимаются как разделитель слов); следовательно, коды букв могут оканчиваться на 0 или 00 (до признака конца знака).
Суть проблемы состоит в нахождении такого варианта кодирования сообщения, при котором последующее выделение из него каждого отдельного знака оказывается однозначным без специальных указателей разделения знаков. Наиболее простыми и употребимыми кодами такого типа являются так называемые префиксные коды, которые удовлетворяют следующему условию (условию фано): неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом (префиксом) какого-либо иного более длинного кода
Если условие фано выполняется, то при прочтении (расшифровке) закодированного сообщения путем сопоставления с таблицей кодов всегда можно точно указать, где заканчивается один код и начинается другой. Таким образом, использование префиксного кодирования позволяет делать сообщение более коротким, поскольку нет необходимости передавать разделители знаков. Однако условие фано не устанавливает способа формирования префиксного кода и, в частности, наилучшего из возможных.
Префиксный код хаффмана способ оптимального префиксного двоичного кодирования был предложен д. Хаффманом
31Алфавитное кодирование с неравной длительностью сигналов. Код морзе.
В качестве примера использования данного варианта кодирования рассмотрим телеграфный код морзе («азбука морзе»). В нем каждой букве или цифре сопоставляется некоторая последовательность кратковременных импульсов - точек и тире, разделяемых паузами. Длительности импульсов и пауз различны: если продолжительность импульса, соответствующего точке, обозначить t, то длительность импульса тире составляет 3t , длительность паузы между точкой и тире t, пауза между буквами слова 3t (длинная пауза), пауза между словами (пробел) – 6t. Таким образом, под знаками кода морзе следует понимать: «•» - «короткий импульс + короткая пауза», «- » - «длинный импульс + короткая пауза», «о» - «длинная пауза», т.е. Код оказывается троичным.
Свой код морзе разработал в 1838 г., т.е. Задолго до исследований относительной частоты появления различных букв в текстах. Однако им был правильно выбран принцип кодирования - буквы, которые встречаются чаще, должны иметь более короткие коды, чтобы сократить общее время передачи. Относительные частоты букв английского алфавита он оценил простым подсчетом литер в ячейках типографской наборной машины. Поэтому самая распространенная английская буква «е» получила код «точка». При составлении кодов морзе для букв русского алфавита учет относительной частоты букв не производился, что, естественно, повысило его избыточность. Произведем оценку избыточности. Для удобства сопоставления данные представим в формате табл. 3.1. (см. Табл. 3.3.). Признак конца буквы («о») в их кодах не отображается, но учтен в величине ki,- длине кода буквы i.
Таблица 3.3
Буква
|
Код
|
Pi *103
|
Ki
|
Буква
|
Код
|
Pi *103
|
Ki
|
Пробел
|
00
|
174
|
2
|
Я
|
. - . -
|
18
|
5
|
О
|
- - -
|
90
|
4
|
Ы
|
- . - -
|
16
|
5
|
Е
|
•
|
72
|
2
|
3
|
- - .
|
16
|
4
|
А
|
•-
|
62
|
3
|
Ь,ъ
|
- . . -
|
14
|
5
|
И
|
. .
|
62
|
3
|
Б
|
- . . .
|
14
|
5
|
Т
|
-
|
53
|
2
|
Г
|
- - .
|
13
|
4
|
Н
|
-•
|
53
|
3
|
Ч
|
- - - .
|
12
|
5
|
С
|
. . .
|
45
|
4
|
Й
|
. - - -
|
10
|
5
|
Р
|
. — .
|
40
|
4
|
X
|
....
|
9
|
5
|
В
|
. - -
|
38
|
4
|
Ж
|
. . . _
|
7
|
5
|
Л
|
. - . .
|
35
|
5
|
Ю
|
. . - -
|
6
|
5
|
К
|
- . -
|
28
|
4
|
Ш
|
- - - -
|
6
|
5
|
М
|
- -
|
26
|
2
|
Ц
|
- . - .
|
4
|
5
|
Д
|
- . .
|
25
|
4
|
Щ
|
- - . -
|
3
|
5
|
П
|
. - -
|
23
|
4
|
Э
|
. . _ . .
|
3
|
6
|
У
|
. . -
|
21
|
4
|
Ф
|
. . - .
|
2
|
5
|
Среднее значение длины кода к(r,3) = 3,361. Полагая появление знаков вторичного алфавита равновероятным, получаем среднюю информацию на знак равной i(2) = iog23 = 1,585 бит.
Код морзе имел в недалеком прошлом весьма широкое распространение в ситуациях, когда источником и приемником сигналов являлся человек (не техническое устройство) и на первый план выдвигалась не экономичность кода, а удобство его восприятия человеком.
32Блочное двоичное кодирование. Равномерное двоичное кодирование. Байтовый код.
возможны варианты кодирования, при которых кодовый знак относится сразу к нескольким буквам первичного алфавита (будем называть такую комбинацию блоком) или даже к целому слову первичного языка. Кодирование блоков понижает избыточность. В этом легко убедиться на простом примере.
Пусть имеется словарь некоторого языка, содержащий n=16000 слов (это, безусловно, более чем солидный словарный запас!). Поставим в соответствие каждому слову равномерный двоичный код. Очевидно, длина кода может быть найдена из соотношения к(а,2)>=log2 n>=13,97=14. Следовательно, каждое слово кодируется комбинацией из 14 нулей и единиц - получатся своего рода двоичные иероглифы. Например, пусть слову «информатика» соответствует код 10101011100110, слову «наука» - 00000000000001, а слову «интересная» - 00100000000010; тогда последовательность: 000000000000110101011100110000000000000001 очевидно, будет означать «информатика интересная наука».
Еще более эффективным окажется кодирование в том случае, если сначала установить относительную частоту появления различных слов в текстах и затем использовать код хаффмана. Подобные исследования провел в свое время шеннон: по относительным частотам 8727 наиболее употребительных в английском языке слов он установил, что средняя информация на знак первичного алфавита оказывается равной 2,15 бит. Вместо слов можно кодировать сочетания букв - блоки. В принципе блоки можно считать словами равной длины, не имеющими, однако, смыслового содержания. Удлиняя блоки и применяя код хаффмана теоретически можно добиться того, что средняя информация на знак кода будет сколь угодно приближаться к i∞.
равномерное алфавитное двоичное кодирование. Байтовый код.
В этом случае двоичный код первичного алфавита строится цепочками равной длины, т.е. Со всеми знаками связано одинаковое количество информации равное i(a) = iog2 n. Формировать признак конца знака не требуется, поэтому для определения длины кода можно воспользоваться формулой к(а,2) >= iog2 n. Приемное устройство просто отсчитывает оговоренное заранее количество элементарных сигналов и интерпретирует цепочку (устанавливает, какому знаку она соответствует), соотнося ее с таблицей кодов. Правда, при этом недопустимы сбои, например, пропуск одного элементарного сигнала приведет к сдвигу всей кодовой последовательности и неправильной ее интерпретации; решается проблема путем синхронизации передачи. С другой стороны, применение равномерного кода оказывается одним из средств контроля правильности передачи, поскольку факт поступления лишнего элементарного сигнала или, наоборот, поступление неполного кода сразу интерпретируется как ошибка.
Примером равномерного алфавитного кодирования является телеграфный код бодо, пришедший на смену азбуке морзе. Исходный алфавит должен содержать не более 32-х символов; тогда к(а,2)=iog232=5, т.е. Каждый знак первичного алфавита содержит 5 бит информации и кодируется цепочкой из 5 двоичных знаков. Условие n < 32, очевидно, выполняется для языков, основанных на латинском алфавите, однако в русском алфавите 34 буквы (с пробелом) - именно по этой причине пришлось «сжать» алфавит (как в коде хаффмана) и объединить в один знак «е» и «ё», а также «ъ» и «ь». После такого сжатия n=32, однако, не остается свободных кодов для знаков препинания, поэтому в телеграммах они отсутствуют или заменяются буквенными аббревиатурами; это не является заметным ограничением, поскольку, как указывалось выше, избыточность языка позволяет легко восстановить информационное содержание сообщения. Избыточность кода бодо для русского языка q(r,2) = 0,148, для английского q(е,2) = 0,239. Другим важным для нас примером использования равномерного алфавитного кодирования является представление символьной информации в компьютере.
|
 Скачать 172.5 Kb.
Скачать 172.5 Kb.