2Минеральный вид

• Название: 2Минеральный вид
• Анкор: 1_Mineralo_769_gia_docx_bez_56-58.docx
• Дата: 09.02.2017
• Размер: 7.05 Mb.
• Имя файла: 1_Mineralo_769_gia_docx_bez_56-58.docx
• Тип: Документы; #2486
• страница: 3 из 7

Элементы симметрии бесконечных фигур, их сочетания.
Одним из свойств, присущих кристаллам, является симметрия. Симметрия - (от греческого «соразмерность») - закономерная повторяемость равных фигур или равных частей одной и той же фигуры в пространстве. Две фигуры называются равными, если расстояние между двумя любыми точками одной фигуры равно расстоянию между двумя соответственными точками другой. К элементам симметрии относятся центр симметрии, оси и плоскости симметрии. Центр симметрии – воображаемая точка внутри фигуры, в которой пересекаются и делятся пополам все прямые, соединяющие соответствен-ные точки на поверхности фигуры (рис. 1). В формуле симметрии обозначается символом С (табл. 1). В многограннике, обладающем центром симметрии, каждой грани отвечает другая грань, равная и параллельная первой. Плоскость симметрии – воображаемая плоскость, разделяющая фигуру на две зеркально-равные части (рис. 2). В формуле симметрии обозначается символом P (табл. 1). Плоскости симметрии проходят перпендикулярно граням и рёбрам через их середины или же идут вдоль рёбер, образуя равные углы с одинаковыми гранями и рёбрами. При подсчёте количества плоскостей симметрии в исследуемой фигуре нужно держать её в одном положении, для того чтобы одну и ту же плос-кость не сосчитать несколько раз.Ось симметрии – воображаемая прямая линия (ось), при вращении вокруг которой на 360 фигура совпадает сама с собой n раз. Количество совпадений n – отвечает порядку оси симметрии. Например, если при вращении на 360 вокруг оси фигура совпадает сама с собой через каждые 180, то есть дважды, то порядок оси симметрии – второй; если – через 120, то есть трижды, – третий и т.п. В формуле симметрии ось обозначается символом Ln (табл. 1). В кристаллических многогранниках и их структурах возможны оси симметрии второго, третьего, четвёртого и шестого порядка. Ось симметрии инверсионная – прямая линия (ось), при повороте вокруг которой на определённый угол и последующем её отражении в цен-тральной точке, фигура совпадает сама с собой. В формуле симметрии обозначается символом Lin. Существуют инверсионные оси симметрии четвёртого и шестого порядка.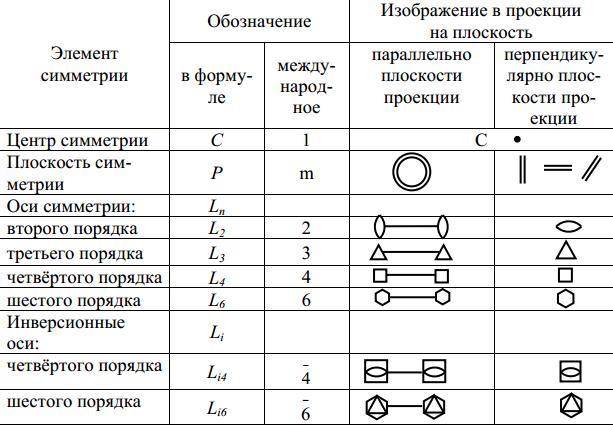



Существует ряд теорем, позволяющих строго математически вывести все возможные совокупности элементов симметрии.

Теорема 1. Линия пересечения двух плоскостей симметрии есть ось симметрии, причём угол поворота вокруг этой оси в два раза больше угла между плоскостями.

Теорема 2. Точка пересечения чётной оси симметрии L2n с перпендикулярной ей плоскостью симметрии есть центр симметрии С.

Теорема 3. Если есть ось симметрии n-го порядка и перпендикулярная ей ось второго порядка, то всего таких осей должно быть n.

Теорема 4. Если есть ось симметрии n-го порядка и вдоль нее проходит плоскость симметрии, то таких плоскостей имеется n.

Теорема 5. Равнодействующей двух пересекающихся осей симметрии является третья ось, проходящая через точку их пересечения.

Теорема 6. Плоскость, проходящая вдоль четной инверсионной оси симметрии, приводит к появлению оси второго порядка, перпендикулярной инверсионной оси и проходящей по биссектрисе угла между плоскостями.

21. Федоровские пространственные группы симметрии (230 групп), принципы их вывода.

При описании симметрии внешней огранки кристаллов используется понятие «точечная группа симметрии».Взаимодействие элементов макросимметрии — зеркальных плоскостей, поворотных и инверсионных осей, центра инверсии — приводит к 32 их сочетаниям — 32 классам (точечным группам) симметрии. Для описания симметрии внутреннего строения кристаллов — их структур — помимо уже перечисленных макроэлементов симметрии потребуются еще трансляционные элементы микросимметрии: прежде всего кристаллическая решетка — главный элемент симметрии бесконечных построек, выявляющий трехмерную периодичность расположения материальных частиц в кристаллическом пространстве, винтовые оси и плоскости скользящего отражения. Взаимодействие всех указанных элементов симметрии приведет к 230 их сочетаниям — 230 пространственным (федоровским) группам симметрии.

Принцип вывода пространственных групп симметрии

Вывод пространственных групп симметрии посредством простого перебора всех сочетаний элементов симметрии и типов решеток Браве будет достаточно сложен и займет много времени. Н. В. Белов предложил более простой и наглядный способ их вывода на основе использования основного принципа Ю. В. Вульфа о фундаментальной роли плоскостей симметрии как порождающих элементов симметрии. Он предложил «оттолкнуться» от 32 точечных групп симметрии, т. е., взяв за основу одну из точечных групп и выделив в не й порождающие элементы симметрии, придавать им разные трансляционные компоненты, сочетания которых с учетом определенного типа решетки Браве и дадут все пространственные группы, подчиненные данной точечной.

В обозначениях пространственных групп на первой позиции регистрируется тип решетки Браве, а затем в символике Германна-Могена (в международной символике, см. параграф 2.9) записывается набор порождающих элементов симметрии с учетом их трансляционных разновидностей. Такие обозначения позволяют отразить различия симметрии кристаллических структур соединений, внешняя огранка которых подчиняется одной точечной группе.

Прежде чем начать вывод пространственных групп с примитивной (Р) решеткой Браве, следует решить, какие трансляционные разновидности плоскостей симметрии возможны на каждой из трех позиций международного символа ромбической голоэдрии. При этом обратим внимание на то, что плоскости скользящего отражения a, b и с с трансляционной компонентой, ориентированной вдоль одной из координатных осей, изменяют свои наименования в зависимости от той или иной ориентации их компонент (i) Обозначения же клиноплоскостей n не меняются в зависимости от их ориентации относительно координатных направлений вследствие того, что их трансляционные компоненты направлены по диагоналям граней элементарной ячейки, т. е. не привязаны к какой-либо определенной координатной оси. Таким образом, перпендикулярно осиХ, т. е. на первой позиции международного символа, могут располагаться плоскости m,n, с или Ь; на второй позиции — перпендикулярно оси Y — плоскости m, n, с или а и на третьей — перпендикулярно оси Z — плоскости m, n, а и Ь. Вывод групп ромбической голоэдрии сведется к определению сочетаний всех возможных перечисленных выше плоскостей. Однако формальная перестановка букв приведет к большому количеству групп,значительно превышающему их реальное число из-за того, что одна и та же группа в разных аспектах будет обозначаться разными символами(рис. 6.20). Избежать указанных трудностей можно, воспользовавшись рекомендациями Н. В. Белова, предложившего следующую схему их вывода.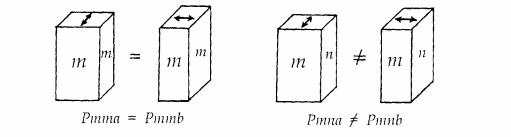








22. Рентгеноструктурный анализ. Формула Вульфа-Брэгга.

Для наблюдения дифракционной картины необходимо, чтобы постоянная решетки была того же порядка, что и длина волны падающего излучения (см. (180.3)). Кристаллы, являясь трехмерными пространственными решетками, имеют постоянную порядка 10^–10 м и, следовательно, непригодны для наблюдения дифракции в видимом свете (l » 5×10^–7 м). Эти факты позволили немецкому физику М. Лауэ (1879—1960) прийти к выводу, что в качестве естественных дифракционных решеток для рентгеновского излучения можно использовать кристаллы, поскольку расстояние между атомами в кристаллах одного порядка с l рентгеновского излучения (»10^–12¸10^–8 м).

Простой метод расчета дифракции рентгеновского излучения от кристаллической решетки предложен независимо друг от друга Г. В. Вульфом (1863—1925) и английскими физиками Г. и Л. Брэггами (отец (1862—1942) и сын (1890—1971)). Они предположили, что дифракция рентгеновского излучения является результатом его отражения от системы параллельных кристаллографических плоскостей (плоскостей, в которых лежат узлы (атомы) кристаллической решетки).

Представим кристаллы в виде совокупности параллельных кристаллографических плоскостей (рис. 264), отстоящих друг от друга на расстоянии d. Пучок параллельных монохроматических рентгеновских лучей (1, 2) падает подуглом скольжения q(уголмежду направлением падающих лучей и кристаллографической плоскостью) и возбуждает атомы кристаллической решетки, которые становятся источниками когерентных вторичных волн 1' и 2', интерферирующих между собой, подобно вторичным волнам, от щелей дифракционной решетки. Максимумы интенсивности (дифракционные максимумы) наблюдаются в тех направлениях, в которых все отраженные атомными плоскостями волны будут находиться в одинаковой фазе. Эти направления удовлетворяютформуле Вульфа — Брэггов

т. е. при разности хода между двумя лучами, отраженными от соседних кристаллографических плоскостей, кратной целому числу длин волн А, наблюдается дифракционный максимум.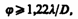



При произвольном направлении падения монохроматического рентгеновского излучения на кристалл дифракция не возникает. Чтобы ее наблюдать, надо, поворачивая кристалл, найти угол скольжения. Дифракционная картина может быть получена и при произвольном положении кристалла, для чего нужно пользоваться непрерывным рентгеновским спектром, испускаемым рентгеновской трубкой. Тогда для таких условий опыта всегда найдутся длины волн l, удовлетворяющие условию (182.1).

Формула Вульфа — Брэггов используется при решении двух важных задач:

1. Наблюдая дифракцию рентгеновских лучей известной длины волны на кристаллической структуре неизвестного строения и измеряя q и т, можно найти межплоскостное расстояние (d), т.е. определить структуру вещества. Этот метод лежит в основе рентгеноструктурного анализа. Формула Вульфа — Брэггов остается справедливой и при дифракции электронов и нейтронов. Методы исследования структуры вещества, основанные на дифракции электронов и нейтронов, называются соответственно электронографией и нейтронографией.

2. Наблюдая дифракцию рентгеновских лучей неизвестной длины волны на кристаллической структуре при известном d и измеряя qит, можно найти длину волны падающего рентгеновского излучения. Этот метод лежит в основе рентгеновской спектроскопии.

23. Правило Гольшмидта (многообразие кристаллических структур).

Правило Гольдшмидта, названное по её открывателю Гольдшмидту, говорит о том, что полный изоморфизм возможен лишь между атомами, ионные радиусы которых различаются на 10-15 %. Правило было открыто в 1926 г.

Правило Магнуса-Гольдшмидта определяет координационное число катиона в зависимости от отношения радиуса катиона к радиусу аниона.

Координационное число	Координационный полиэдр	Радиус катиона/радиус аниона
12	кубооктаэдр	1,000
9	центрированная по вертикальным граням тригональная призма	0,732
8	куб	0,732
8	квадратная антипризма	0,645
7	октаэдр с одной центрированной гранью	0,592
6	октаэдр	0,414
4	тетраэдр	0,215
3	треугольник	0,155

24. Типы химических связей в кристаллах.

Все атомы в кристаллических структурах взаимосвязаны, то и координационные числа, и тип построек из тех или иных атомов, и другие характеристики структур являются функцией взаимодействий между атомами, т. е. функцией химической связи между ними. Концепция химической связи — важнейшего понятия химии — лежит в основе всех остальных ее базовых понятий и является одной из центральных в науках о строении вещества.Нужно помнить, что химическая связь — это взаимодействие атомов одного и того же или разных химических элементов, в процессе которого происходит перестройка электронных оболочек связывающихся атомов с одновременным образованием единого электронного облака, сопровождающимся понижением энергии всей системы. И независимо от агрегатного состояния вещества химическая связь всегда электростатическая и может быть описана с помощью представлений о валентных электронах связанных атомов.Поскольку энергия взаимодействий атомов характеризуется большим диапазоном, химические связи между частицами в структурах принято делить на следующие типы: металлические, ионные, ковалентные, вандер-ваальсовы и водородные.

Металлическая связь характерна для элементов первых групп периодической системы и интерметаллов. Эта связь осуществляется взаимодействием свободных электронов и положительно заряженных атомных ядер. Металлический кристалл можно представить как решетку из положительно заряженных атомных ядер, погруженных в отрицательно заряженный «газ», состоящий из свободных электронов. Все атомы отдают свои электроны в общее пользование, т. е. все свободные электроны обобществляются и легко перемещаются внутри структуры, не нарушая типа химической связи. Для металлических структур характерны большие координационные числа (КЧ = 8, 12), плотные и плотнейшие упаковки частиц, а также ряд специфических свойств, таких как высокие электропроводность и теплопроводность, ковкость, невысокие температуры плавления и кипения, объясняемых существованием свободно перемещающихся электронов, слабо связанных с атомными ядрами металлов.

Ионная связь.В узлах кристаллической решётки помещаются положительно и отрицательно заряженные ионы.Силы взаимодействия между узлами являются в основном электростатическими (кулоновскими). Связь между такими частицами называется гетерополярной или ионной.Кристаллы с ионной связью при низких температурах являются диэлектриками. При температурах близких к температуре плавления они становятся проводниками электричества. Примером кристаллов с ионной решёткой являются кристаллы каменной соли (NaCl). Это связь, при которой внешние электроны атомов первого элемента переходят на внешние орбиты атомов другого элемента образуя устойчивые конфигурации.

Кристаллы с ковалентной связью диэлектрики или полупроводники. Типичными примерами атомных кристаллов могут служить алмаз, германий и кремний.

В узлах кристаллической решётки помещаются определённым образом ориентированные молекулы. Силы связи между молекулами в кристалле имеют ту же природу, что и силы притяжения между молекулами, приводящие к отклонению газов от идеальности. По этой причине их называют ван-дер-ваальсовскими силами.Для кристаллов с молекулярными связями характерны низкие температуры плавления и высокая сжимаемость.

Особая разновидность молекулярной связи — водородная связь. При определённых условиях атом водорода может быть связан довольно прочно с двумя другими атомами. Имея лишь одну стабильную орбиталь, атом водорода способен образовывать только одну ковалентную связь. Эта связь может, однако, резонировать между двумя положениями. Наибольшее значение имеют те водородные связи, которые образуются между двумя сильно электроотрицательными атомами, в особенности между атомами азота, кислорода и фтора. Молекулярные связи образуют, например, следующие вещества: H₂, N₂, O₂, CO₂, H₂O.

25. Атомные и ионные радиусы. Явления поляризации в кристаллах.
Для вычисления ионных радиусов атомов всех элементов необходимо сначала определить хотя бы один из них и далее, используя правило аддитивности R_ab =r_a+r_b, рассчитать все остальные, вычитая из значения межатомного расстояния величину известного радиуса. Согласно ионной модели В. Косселя (1927 г.), отрицательные частицы — электроны, отрываясь от одного атома и тем самым превращая его в катион (К), переносятся к другому атому, сообщая ему отрицательный заряд (делая его анионом (А)) и этим увеличивая его размер.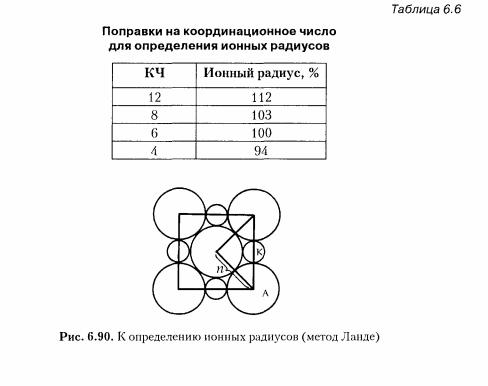